北师大版八年级下册 2 直角三角形课件(共18张ppt)
文档属性
| 名称 | 北师大版八年级下册 2 直角三角形课件(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 23:28:53 | ||
图片预览




文档简介
(共18张PPT)
14.1 勾股定理
第1课时 直角三角形三边的关系
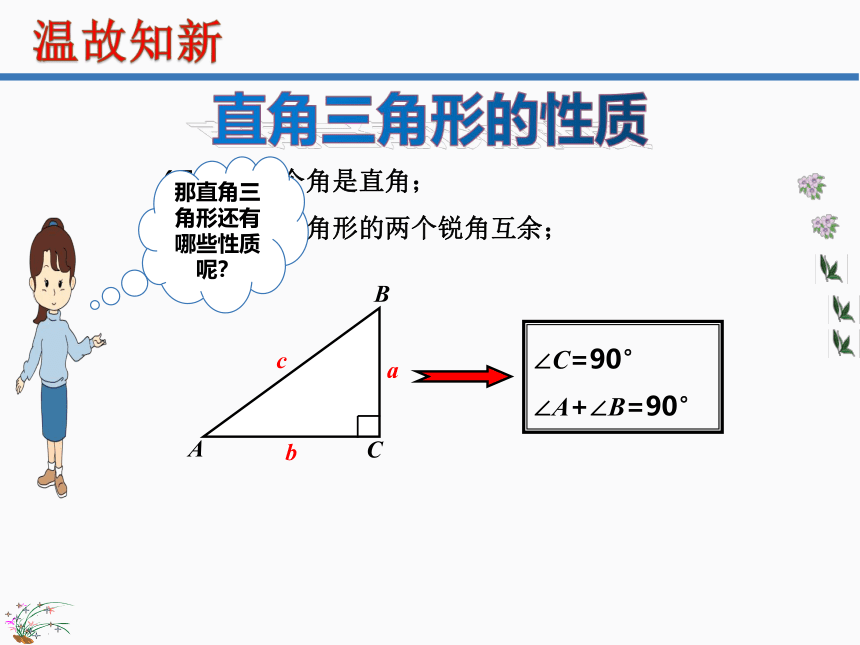
直角三角形的性质
(Ⅰ)有一个角是直角;
A
B
C
a
b
c
∠C=90°
∠A+∠B=90°
(Ⅱ)直角三角形的两个锐角互余;
那直角三角形还有哪些性质呢?
温故知新
温故知新
三角形的三边关系:a-ba
b
c
b
a
c
直角三角形的三边关系有什么特殊的性质呢?
三角形边的性质
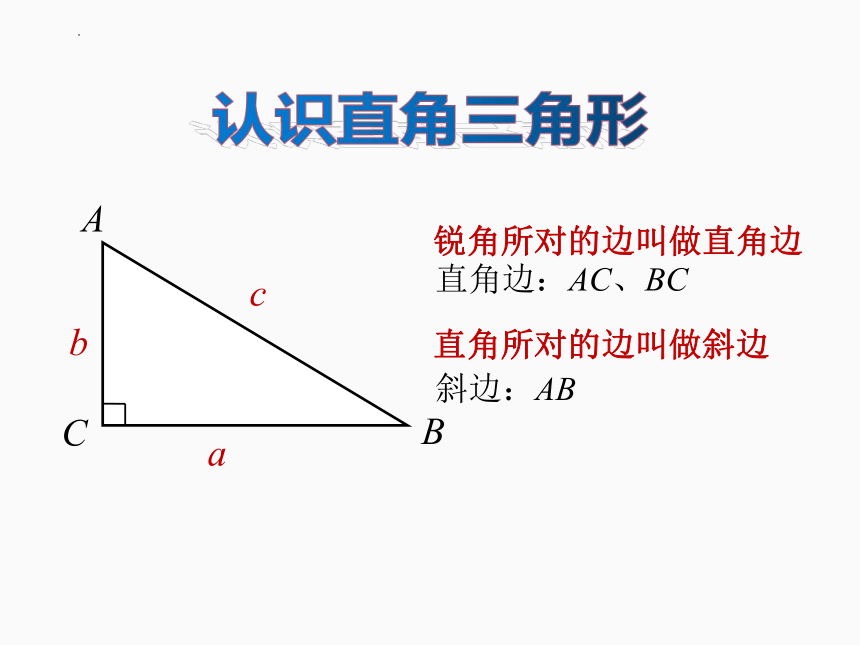
认识直角三角形
b
a
c
A
B
C
直角所对的边叫做斜边
锐角所对的边叫做直角边
直角边:AC、BC
斜边:AB
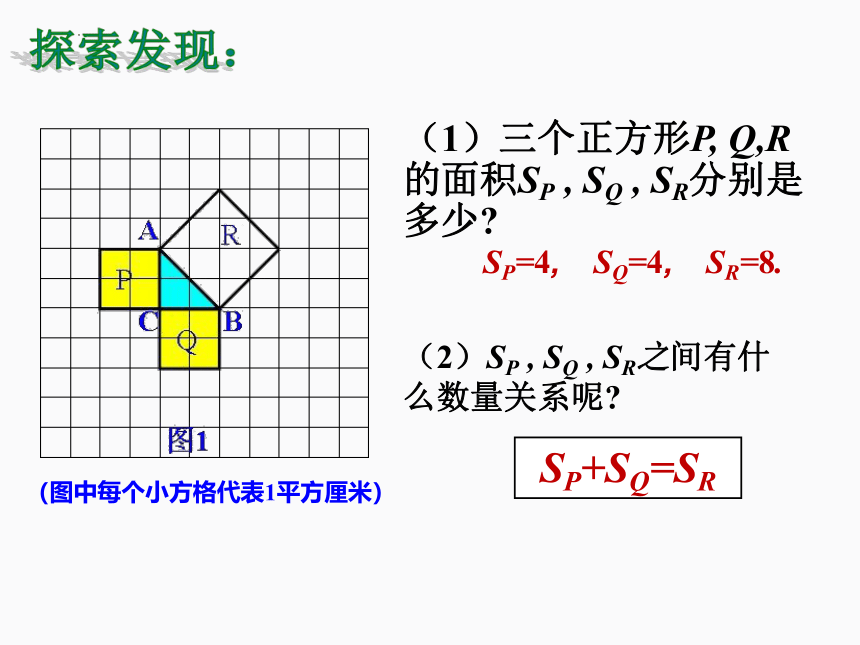
(图中每个小方格代表1平方厘米)
探索发现:
(1)三个正方形P, Q,R的面积SP , SQ , SR分别是多少
SP=4, SQ=4, SR=8.
(2)SP , SQ , SR之间有什么数量关系呢
SP+SQ=SR
P
Q
R
正方形P的面积为_____,
正方形Q的面积为_____,
正方形R的面积为_____.
9
16
25
假设每个小正方形的面积都为1.
思考:三个正方形P, Q,R面积之间有什么等量关系呢
SP+SQ=SR.
割补法
探索发现:
思考:
直角三角形三边a,b,c之间有什么等量关系
P
Q
R
a2 + b2 = c2
SP+SQ=SR
a
b
c
直角三角形两直角边的平方和等于斜边的平方.
探索发现:
A
B
C
c
a
b
猜想 如果直角三角形的两条直角边长分别为a,b,
斜边长为 c,那么a2+b2=c2.
探索发现:
摆一摆,拼一拼,利用以下四个全等的直角三角形拼一个正方形.
c
a
b
c
a
b
c
a
b
c
a
b
动手实践 验证猜想
(1)这个大正方形的边长是多少?
(2)如何表示大正方形的面积?
b
b
b
b
c
c
c
c
a
a
a
a
面积法
证明结论
a
b
c
a
b
c
a
b
c
a
b
c
证明结论
(1)这个大正方形的边长是多少?
(2)如何表示大正方形的面积?
直角三角形三边的关系
直角三角形两直角边的平方和等于斜边的平方.
又名:勾股定理
勾股定理结论变形
直角三角形两直角边的平方和等于斜边的平方.
B
A
C
a
c
b
勾股史话
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
例 1
在Rt△ABC中,∠B=90°,AB=6,BC=8,求AC.
C
A
B
变式拓展
变式1:在Rt△ABC中,∠B=90°,AC=10,BC=8,求AB;
变式2:在Rt△ABC中,∠B=90°,AC=10,AB=6,求BC;
变式3:在Rt△ABC中,∠B=90°,其中一条边为5,另一条边为3,求第三边.
在 中
学以致用
直角三角形三边的关系
注意:(1)勾股定理是研究直角三角形三边之间的关系,只在直角三角形 中成立.
(2)运用勾股定理时要分清直角边和斜边,然后再使用;若没有告
诉斜边的情况下,经常有两解,勿漏解.
(3)勾股定理将“形”转化为“数”,已知直角三角形任意两边,
可以求出第三边.
例如
A
C
B
a
c
b
C
B
A
c
b
a
直角三角形两直角边的平方和等于斜边的平方.
我的收获是……
这节课我学到了什么?
我还有……的疑惑
畅谈收获
小 结
14.1 勾股定理
第1课时 直角三角形三边的关系
直角三角形的性质
(Ⅰ)有一个角是直角;
A
B
C
a
b
c
∠C=90°
∠A+∠B=90°
(Ⅱ)直角三角形的两个锐角互余;
那直角三角形还有哪些性质呢?
温故知新
温故知新
三角形的三边关系:a-b
b
c
b
a
c
直角三角形的三边关系有什么特殊的性质呢?
三角形边的性质
认识直角三角形
b
a
c
A
B
C
直角所对的边叫做斜边
锐角所对的边叫做直角边
直角边:AC、BC
斜边:AB
(图中每个小方格代表1平方厘米)
探索发现:
(1)三个正方形P, Q,R的面积SP , SQ , SR分别是多少
SP=4, SQ=4, SR=8.
(2)SP , SQ , SR之间有什么数量关系呢
SP+SQ=SR
P
Q
R
正方形P的面积为_____,
正方形Q的面积为_____,
正方形R的面积为_____.
9
16
25
假设每个小正方形的面积都为1.
思考:三个正方形P, Q,R面积之间有什么等量关系呢
SP+SQ=SR.
割补法
探索发现:
思考:
直角三角形三边a,b,c之间有什么等量关系
P
Q
R
a2 + b2 = c2
SP+SQ=SR
a
b
c
直角三角形两直角边的平方和等于斜边的平方.
探索发现:
A
B
C
c
a
b
猜想 如果直角三角形的两条直角边长分别为a,b,
斜边长为 c,那么a2+b2=c2.
探索发现:
摆一摆,拼一拼,利用以下四个全等的直角三角形拼一个正方形.
c
a
b
c
a
b
c
a
b
c
a
b
动手实践 验证猜想
(1)这个大正方形的边长是多少?
(2)如何表示大正方形的面积?
b
b
b
b
c
c
c
c
a
a
a
a
面积法
证明结论
a
b
c
a
b
c
a
b
c
a
b
c
证明结论
(1)这个大正方形的边长是多少?
(2)如何表示大正方形的面积?
直角三角形三边的关系
直角三角形两直角边的平方和等于斜边的平方.
又名:勾股定理
勾股定理结论变形
直角三角形两直角边的平方和等于斜边的平方.
B
A
C
a
c
b
勾股史话
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
例 1
在Rt△ABC中,∠B=90°,AB=6,BC=8,求AC.
C
A
B
变式拓展
变式1:在Rt△ABC中,∠B=90°,AC=10,BC=8,求AB;
变式2:在Rt△ABC中,∠B=90°,AC=10,AB=6,求BC;
变式3:在Rt△ABC中,∠B=90°,其中一条边为5,另一条边为3,求第三边.
在 中
学以致用
直角三角形三边的关系
注意:(1)勾股定理是研究直角三角形三边之间的关系,只在直角三角形 中成立.
(2)运用勾股定理时要分清直角边和斜边,然后再使用;若没有告
诉斜边的情况下,经常有两解,勿漏解.
(3)勾股定理将“形”转化为“数”,已知直角三角形任意两边,
可以求出第三边.
例如
A
C
B
a
c
b
C
B
A
c
b
a
直角三角形两直角边的平方和等于斜边的平方.
我的收获是……
这节课我学到了什么?
我还有……的疑惑
畅谈收获
小 结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
