2022年人教版小学数学六年级下册 第3单元圆柱课后练(含答案)
文档属性
| 名称 | 2022年人教版小学数学六年级下册 第3单元圆柱课后练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 68.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 06:45:33 | ||
图片预览




文档简介
2022年人教版小学数学六年级下册
第3单元 圆柱 课后练
一、选择题 (将正确答案的字母填在括号里)
1.一个圆柱和一个圆锥高的比是1:4,底面积的比是2:1,体积的比是( )。
A.2:1 B.4:3 C.3:2 D.2:3
2.把长2米的圆柱形木料锯成4段小圆柱形木料,表面积增加了60平方分米,原来木料的体积是( )立方分米。
A.40 B.200 C.20 D.400
3.冬天护林工人给圆柱形的树干的下端涂防蛀涂料,那么粉刷树干的面积是指( )
A.底面积 B.侧面积 C.表面积 D.体积
4.圆柱的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来的( )倍。
A.4 B.8 C.16
5.如图,把一个直径为4cm,高为8cm的圆柱,沿底面直径切开,表面积增加了多少平方厘米?答案正确的是( )
A.100.48 cm2 B.64cm2 C.32 cm2
二、判断题 (对的在括号里打√,错的打 )
6.如果两个圆柱的侧面积相等,那么它们的底面周长也相等。( )
7.圆锥的高是圆柱高的3倍,它们的体积一定相等。( )
8.表面积相等的两个圆柱,体积也一定相等。 ( )
9.圆柱的底面半径扩大到原来的3倍,高缩小到原来的 ,体积不变。( )
10.把圆柱的底面直径扩大到原来的2倍,高缩小到原来的 ,这个圆柱的体积不变。( )
三、填空题
11.圆柱的侧面展开图是一个边长为12.56厘米的正方形,圆柱的体积是 立方厘米。
12.把一个高2dm的圆柱钢材铸成与它底面积相等的圆锥体,这个圆锥体的高是 dm。
13.小华学校大厅有8根大小一样的圆柱形大理石石柱,每根柱子的半径是5分米,高6米,如果要清洗这些柱子,清洗的面积是 平方米。
14.把一个底面直径为3厘米、高是5厘米的圆柱体沿直径切割成两个半圆柱,表面积增加了 。
15.一个圆柱体,底面圆的周长是6.28分米,侧面积是12.56平方分米,这个圆柱体的高是 分米。
四、计算题
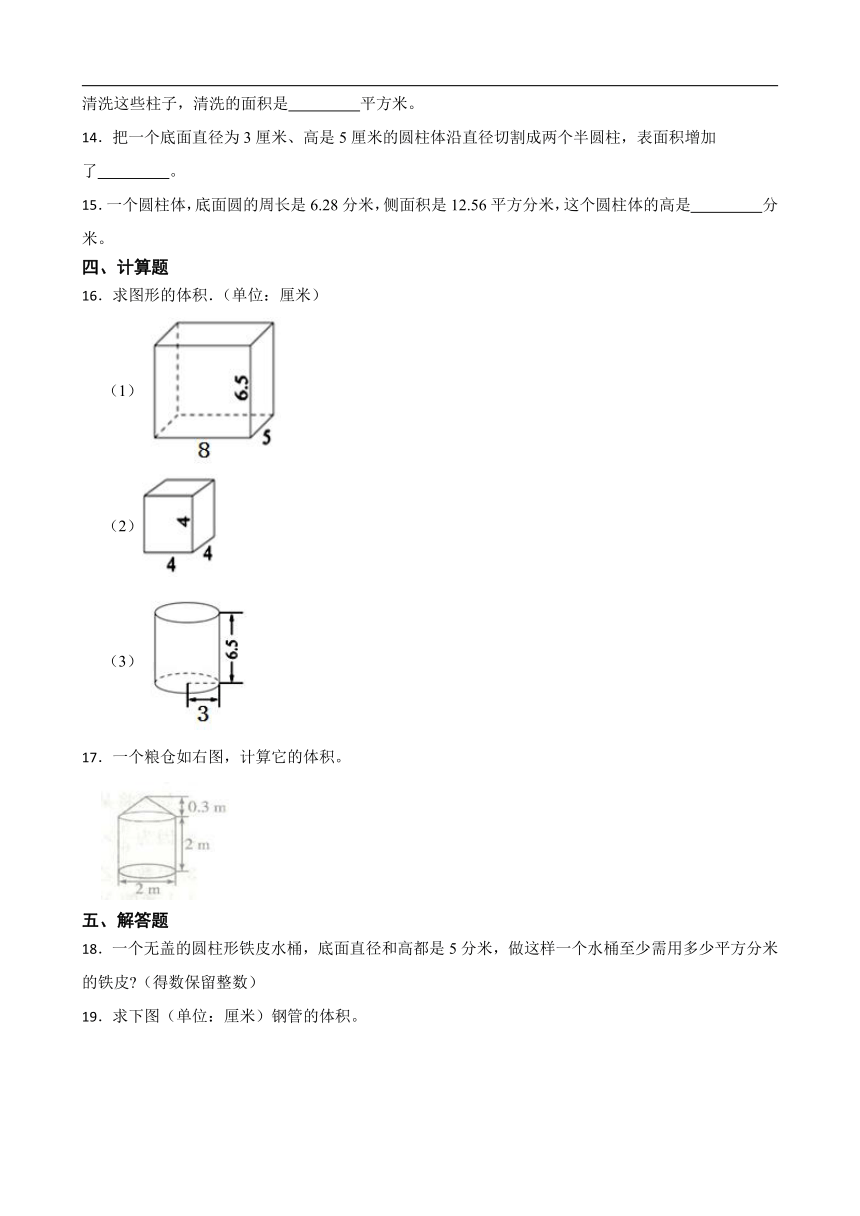
16.求图形的体积.(单位:厘米)
(1)
(2)
(3)
17.一个粮仓如右图,计算它的体积。
五、解答题
18.一个无盖的圆柱形铁皮水桶,底面直径和高都是5分米,做这样一个水桶至少需用多少平方分米的铁皮 (得数保留整数)
19.求下图(单位:厘米)钢管的体积。
20.种好以后的几天,每天要给草地浇水约1.57立方米,一个内底面直径和高都是2米的圆柱体水池装满水能浇几天?
答案解析部分
1.【答案】C
【考点】圆柱的体积(容积);圆锥的体积(容积);比的化简与求值
【解析】【解答】解:圆柱的体积:圆锥的体积=(2×1):(1×4×)
=2:
=(2×3):(×3)
=6:4
=(6÷2):(4÷2)
=3:2。
故答案为:C。
【分析】圆柱的体积=圆柱的底面积×圆柱的高,圆锥的体积=圆锥的底面积×圆锥的高×,即可得出圆柱的体积:圆锥的体积=(2×1):(1×4×),再根据比的基本性质进行化简即可得出答案。
2.【答案】B
【考点】圆柱的侧面积、表面积;圆柱的体积(容积)
【解析】【解答】解:60÷6=10(平方分米);
2米=20分米;
10×20=200(立方分米)。
故答案为:B。
【分析】根据题意,把圆柱形木料锯成4段,增加了6个底面积,表面积也就增加了6个底面积的大小,据此求出一个底面积的大小,再根据圆柱的体积等于底面积乘高,把高的单位化成分米即可求出原木料的体积。
3.【答案】B
【考点】圆柱的侧面积、表面积
【解析】【解答】解:粉刷树干的面积是指树干的侧面积。
故答案为:B。
【分析】树干是圆柱形的,涂防蛀涂料的部分就是圆柱形树干的侧面积。
4.【答案】A
【考点】圆柱的体积(容积)
【解析】【解答】解:底面半径扩大到原来的2倍,底面积会扩大到原来的4倍,高不变,体积就扩大到原来的4倍。
故答案为:A。
【分析】圆柱的体积=底面积×高,高不变,底面积扩大多少倍,体积就会扩大多少倍。
5.【答案】B
【考点】圆柱的特征
【解析】【解答】解:8×4×2=64(平方厘米),所以表面积增加了64平方厘米。
故答案为:B。
【分析】增加的面积就是2个长是8厘米,宽是4厘米的长方形的面积,其中长方形的面积=长×宽。
6.【答案】(1)错误
【考点】圆柱的侧面积、表面积
【解析】【解答】 如果两个圆柱的侧面积相等,它们的底面周长不一定相等 。
故答案为:错误。
【分析】圆柱的侧面积公式:S=Ch,决定圆柱侧面积大小有底面周长和高这两个因素,当侧面积相等时,高不相等,底面周长也不相等。
7.【答案】(1)错误
【考点】圆柱的体积(容积);圆锥的体积(容积)
【解析】【解答】解:圆锥的高是圆柱高的3倍,它们的体积不一定相等。
故答案为:错误。
【分析】假设圆锥的高是3,底面积是2,那么它的体积是2;假设圆柱的高是1,圆柱的底面积是3,那么它的体积是3,所以它们的体积不相等。
8.【答案】(1)错误
【考点】圆柱的侧面积、表面积;圆柱的体积(容积)
【解析】【解答】解:表面积相等的两个圆柱,体积不一定相等。
故答案为:错误。
【分析】表面积相等的两个圆柱,它们的底面半径和高却不一定相等,所以它们的体积也不一定相等。
9.【答案】(1)错误
【考点】圆柱的体积(容积)
【解析】【解答】 圆柱的底面半径扩大到原来的3倍,高缩小到原来的 ,体积不变。这个说法是错误的。
故答案为:错误。
【分析】当圆柱的高不变,圆柱的底面半径扩大到原来的3倍时,底面积扩大到原来的9倍,即体积扩大到原来的9倍;当底面半径不变,高缩小到原来的 时,体积缩小到原来的;所以,体积变为原来的倍。
10.【答案】(1)错误
【考点】圆柱的体积(容积)
【解析】【解答】设原直径为2,则现直径为4;设原高为2,则现高为1。
原体积:π(2÷2)2×2=2π,现体积:π(4÷2)2×1=4π,现体积÷原体积=2。
所以原说法错误。
故答案为:错误。
【分析】圆柱的体积=πr2h。
11.【答案】157.7536
【考点】圆柱的体积(容积)
【解析】【解答】解:12.56÷3.14÷2=2(厘米)
体积:3.14×22×12.56
=3.14×4×12.56
=157.7536(立方厘米)
故答案为:157.7536。
【分析】因为侧面展开是正方形,所以这个圆柱的底面周长和高相等。用正方形的边长(也就是圆柱的底面周长)除以3.14再除以2求出底面半径,然后用底面积乘高求出圆柱的体积。
12.【答案】6
【考点】圆柱的体积(容积);圆锥的体积(容积)
【解析】【解答】解:这个圆锥体的高是2×3=6dm。
故答案为:6。
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高× ,因为圆柱和圆锥的底面积和体积都相等,那么圆锥的高=圆柱的高×3。
13.【答案】150.72
【考点】圆柱的侧面积、表面积
【解析】【解答】解:5分米=0.5米,
3.14×0.5×2×6×8
=3.14×48
=150.72(平方米)
故答案为:150.72。
【分析】只需要清洁柱子的侧面积,因此用底面周长乘高求出侧面积,再乘8求出清洁的总面积即可。注意统一单位。
14.【答案】30cm
【考点】圆柱的特征;圆柱的侧面积、表面积
【解析】【解答】3×5=15(平方厘米),15×2=30(平方厘米)
故答案为:30cm2。
【分析】 表面积增加两个长方形的面积,增加了多少=底面直径×高×2。
15.【答案】2
【考点】圆柱的侧面积、表面积
【解析】【解答】解:12.56÷6.28=2(分米)。
故答案为:2。
【分析】圆柱体的高=侧面积÷底面周长。
16.【答案】(1)8×5×6.5
=40×6.5
=260(立方厘米)
(2)4×4×4
=16×4
=64(立方厘米)
(3)3.14×32×6.5
=3.14×9×6.5
=28.26×6.5
=183.69(立方厘米)
【考点】圆柱的体积(容积)
【解析】【分析】(1)长方体的体积=长×宽×高;
(2)正方体的体积=棱长×棱长×棱长;
(3)圆柱的体积=底面积×高;其中,底面积=π×半径2。
17.【答案】解:3.14×( )2×(2+0.3× )=6.594m3
【考点】圆柱的体积(容积);圆锥的体积(容积);组合体的体积的巧算
【解析】【分析】观察图可知,粮仓的体积=圆柱的体积+圆锥的体积,根据圆柱的体积V=πr2h,圆锥的体积V=πr2h,据此列式解答.
18.【答案】解:3.14×2.52+3.14×5×5=98.125≈98(平方分米)
答:做这样一个水桶至少需用98平方分米的铁皮。
【考点】圆柱的侧面积、表面积
【解析】【分析】因为无盖,所以只有一个底面,根据圆面积公式计算底面积,用底面周长乘高求出侧面积,相加后就是需要铁皮的面积。
19.【答案】解:10÷2=5(厘米);
8÷2=4(厘米);
3.14×(52-42)×100
=3.14×(25-16)×100
=3.14×9×100
=28.26×100
=2826(立方厘米).
【考点】圆柱的体积(容积)
【解析】【分析】根据题意可知,这根钢管的体积=底面积×高,底面是一个圆环,根据圆环的面积S=π(R2-r2),据此先求出底面积,然后乘钢管的长度,即可得到这根钢管的体积,据此列式解答.
20.【答案】解:2÷2=1(米)
3.14×12×2
=3.14×2
=6.28(立方米)
6.28÷1.57=4(天)
答: 一个内底面直径和高都是2米的圆柱体水池装满水能浇4天。
【考点】圆柱的体积(容积)
【解析】【分析】根据题意可知,先求出这个圆柱体水池的容积,V=πr2h,据此列式计算;然后用水池的容积÷每天浇水的体积=可以浇水的天数,据此列式解答。
试题分析部分
1、试卷总体分布分析
总分:60分
分值分布 客观题(占比) 25.0(41.7%)
主观题(占比) 35.0(58.3%)
题量分布 客观题(占比) 15(75.0%)
主观题(占比) 5(25.0%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 5(25.0%) 5.0(8.3%)
解答题 3(15.0%) 15.0(25.0%)
计算题 2(10.0%) 20.0(33.3%)
单选题 5(25.0%) 10.0(16.7%)
判断题 5(25.0%) 10.0(16.7%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (100.0%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 圆柱的侧面积、表面积 16.0(26.7%) 2,3,6,8,13,14,15,18
2 圆锥的体积(容积) 10.0(16.7%) 1,7,12,17
3 圆柱的体积(容积) 46.0(76.7%) 1,2,4,7,8,9,10,11,12,16,17,19,20
4 组合体的体积的巧算 5.0(8.3%) 17
5 圆柱的特征 3.0(5.0%) 5,14
6 比的化简与求值 2.0(3.3%) 1
第3单元 圆柱 课后练
一、选择题 (将正确答案的字母填在括号里)
1.一个圆柱和一个圆锥高的比是1:4,底面积的比是2:1,体积的比是( )。
A.2:1 B.4:3 C.3:2 D.2:3
2.把长2米的圆柱形木料锯成4段小圆柱形木料,表面积增加了60平方分米,原来木料的体积是( )立方分米。
A.40 B.200 C.20 D.400
3.冬天护林工人给圆柱形的树干的下端涂防蛀涂料,那么粉刷树干的面积是指( )
A.底面积 B.侧面积 C.表面积 D.体积
4.圆柱的高不变,底面半径扩大到原来的2倍,它的体积就扩大到原来的( )倍。
A.4 B.8 C.16
5.如图,把一个直径为4cm,高为8cm的圆柱,沿底面直径切开,表面积增加了多少平方厘米?答案正确的是( )
A.100.48 cm2 B.64cm2 C.32 cm2
二、判断题 (对的在括号里打√,错的打 )
6.如果两个圆柱的侧面积相等,那么它们的底面周长也相等。( )
7.圆锥的高是圆柱高的3倍,它们的体积一定相等。( )
8.表面积相等的两个圆柱,体积也一定相等。 ( )
9.圆柱的底面半径扩大到原来的3倍,高缩小到原来的 ,体积不变。( )
10.把圆柱的底面直径扩大到原来的2倍,高缩小到原来的 ,这个圆柱的体积不变。( )
三、填空题
11.圆柱的侧面展开图是一个边长为12.56厘米的正方形,圆柱的体积是 立方厘米。
12.把一个高2dm的圆柱钢材铸成与它底面积相等的圆锥体,这个圆锥体的高是 dm。
13.小华学校大厅有8根大小一样的圆柱形大理石石柱,每根柱子的半径是5分米,高6米,如果要清洗这些柱子,清洗的面积是 平方米。
14.把一个底面直径为3厘米、高是5厘米的圆柱体沿直径切割成两个半圆柱,表面积增加了 。
15.一个圆柱体,底面圆的周长是6.28分米,侧面积是12.56平方分米,这个圆柱体的高是 分米。
四、计算题
16.求图形的体积.(单位:厘米)
(1)
(2)
(3)
17.一个粮仓如右图,计算它的体积。
五、解答题
18.一个无盖的圆柱形铁皮水桶,底面直径和高都是5分米,做这样一个水桶至少需用多少平方分米的铁皮 (得数保留整数)
19.求下图(单位:厘米)钢管的体积。
20.种好以后的几天,每天要给草地浇水约1.57立方米,一个内底面直径和高都是2米的圆柱体水池装满水能浇几天?
答案解析部分
1.【答案】C
【考点】圆柱的体积(容积);圆锥的体积(容积);比的化简与求值
【解析】【解答】解:圆柱的体积:圆锥的体积=(2×1):(1×4×)
=2:
=(2×3):(×3)
=6:4
=(6÷2):(4÷2)
=3:2。
故答案为:C。
【分析】圆柱的体积=圆柱的底面积×圆柱的高,圆锥的体积=圆锥的底面积×圆锥的高×,即可得出圆柱的体积:圆锥的体积=(2×1):(1×4×),再根据比的基本性质进行化简即可得出答案。
2.【答案】B
【考点】圆柱的侧面积、表面积;圆柱的体积(容积)
【解析】【解答】解:60÷6=10(平方分米);
2米=20分米;
10×20=200(立方分米)。
故答案为:B。
【分析】根据题意,把圆柱形木料锯成4段,增加了6个底面积,表面积也就增加了6个底面积的大小,据此求出一个底面积的大小,再根据圆柱的体积等于底面积乘高,把高的单位化成分米即可求出原木料的体积。
3.【答案】B
【考点】圆柱的侧面积、表面积
【解析】【解答】解:粉刷树干的面积是指树干的侧面积。
故答案为:B。
【分析】树干是圆柱形的,涂防蛀涂料的部分就是圆柱形树干的侧面积。
4.【答案】A
【考点】圆柱的体积(容积)
【解析】【解答】解:底面半径扩大到原来的2倍,底面积会扩大到原来的4倍,高不变,体积就扩大到原来的4倍。
故答案为:A。
【分析】圆柱的体积=底面积×高,高不变,底面积扩大多少倍,体积就会扩大多少倍。
5.【答案】B
【考点】圆柱的特征
【解析】【解答】解:8×4×2=64(平方厘米),所以表面积增加了64平方厘米。
故答案为:B。
【分析】增加的面积就是2个长是8厘米,宽是4厘米的长方形的面积,其中长方形的面积=长×宽。
6.【答案】(1)错误
【考点】圆柱的侧面积、表面积
【解析】【解答】 如果两个圆柱的侧面积相等,它们的底面周长不一定相等 。
故答案为:错误。
【分析】圆柱的侧面积公式:S=Ch,决定圆柱侧面积大小有底面周长和高这两个因素,当侧面积相等时,高不相等,底面周长也不相等。
7.【答案】(1)错误
【考点】圆柱的体积(容积);圆锥的体积(容积)
【解析】【解答】解:圆锥的高是圆柱高的3倍,它们的体积不一定相等。
故答案为:错误。
【分析】假设圆锥的高是3,底面积是2,那么它的体积是2;假设圆柱的高是1,圆柱的底面积是3,那么它的体积是3,所以它们的体积不相等。
8.【答案】(1)错误
【考点】圆柱的侧面积、表面积;圆柱的体积(容积)
【解析】【解答】解:表面积相等的两个圆柱,体积不一定相等。
故答案为:错误。
【分析】表面积相等的两个圆柱,它们的底面半径和高却不一定相等,所以它们的体积也不一定相等。
9.【答案】(1)错误
【考点】圆柱的体积(容积)
【解析】【解答】 圆柱的底面半径扩大到原来的3倍,高缩小到原来的 ,体积不变。这个说法是错误的。
故答案为:错误。
【分析】当圆柱的高不变,圆柱的底面半径扩大到原来的3倍时,底面积扩大到原来的9倍,即体积扩大到原来的9倍;当底面半径不变,高缩小到原来的 时,体积缩小到原来的;所以,体积变为原来的倍。
10.【答案】(1)错误
【考点】圆柱的体积(容积)
【解析】【解答】设原直径为2,则现直径为4;设原高为2,则现高为1。
原体积:π(2÷2)2×2=2π,现体积:π(4÷2)2×1=4π,现体积÷原体积=2。
所以原说法错误。
故答案为:错误。
【分析】圆柱的体积=πr2h。
11.【答案】157.7536
【考点】圆柱的体积(容积)
【解析】【解答】解:12.56÷3.14÷2=2(厘米)
体积:3.14×22×12.56
=3.14×4×12.56
=157.7536(立方厘米)
故答案为:157.7536。
【分析】因为侧面展开是正方形,所以这个圆柱的底面周长和高相等。用正方形的边长(也就是圆柱的底面周长)除以3.14再除以2求出底面半径,然后用底面积乘高求出圆柱的体积。
12.【答案】6
【考点】圆柱的体积(容积);圆锥的体积(容积)
【解析】【解答】解:这个圆锥体的高是2×3=6dm。
故答案为:6。
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高× ,因为圆柱和圆锥的底面积和体积都相等,那么圆锥的高=圆柱的高×3。
13.【答案】150.72
【考点】圆柱的侧面积、表面积
【解析】【解答】解:5分米=0.5米,
3.14×0.5×2×6×8
=3.14×48
=150.72(平方米)
故答案为:150.72。
【分析】只需要清洁柱子的侧面积,因此用底面周长乘高求出侧面积,再乘8求出清洁的总面积即可。注意统一单位。
14.【答案】30cm
【考点】圆柱的特征;圆柱的侧面积、表面积
【解析】【解答】3×5=15(平方厘米),15×2=30(平方厘米)
故答案为:30cm2。
【分析】 表面积增加两个长方形的面积,增加了多少=底面直径×高×2。
15.【答案】2
【考点】圆柱的侧面积、表面积
【解析】【解答】解:12.56÷6.28=2(分米)。
故答案为:2。
【分析】圆柱体的高=侧面积÷底面周长。
16.【答案】(1)8×5×6.5
=40×6.5
=260(立方厘米)
(2)4×4×4
=16×4
=64(立方厘米)
(3)3.14×32×6.5
=3.14×9×6.5
=28.26×6.5
=183.69(立方厘米)
【考点】圆柱的体积(容积)
【解析】【分析】(1)长方体的体积=长×宽×高;
(2)正方体的体积=棱长×棱长×棱长;
(3)圆柱的体积=底面积×高;其中,底面积=π×半径2。
17.【答案】解:3.14×( )2×(2+0.3× )=6.594m3
【考点】圆柱的体积(容积);圆锥的体积(容积);组合体的体积的巧算
【解析】【分析】观察图可知,粮仓的体积=圆柱的体积+圆锥的体积,根据圆柱的体积V=πr2h,圆锥的体积V=πr2h,据此列式解答.
18.【答案】解:3.14×2.52+3.14×5×5=98.125≈98(平方分米)
答:做这样一个水桶至少需用98平方分米的铁皮。
【考点】圆柱的侧面积、表面积
【解析】【分析】因为无盖,所以只有一个底面,根据圆面积公式计算底面积,用底面周长乘高求出侧面积,相加后就是需要铁皮的面积。
19.【答案】解:10÷2=5(厘米);
8÷2=4(厘米);
3.14×(52-42)×100
=3.14×(25-16)×100
=3.14×9×100
=28.26×100
=2826(立方厘米).
【考点】圆柱的体积(容积)
【解析】【分析】根据题意可知,这根钢管的体积=底面积×高,底面是一个圆环,根据圆环的面积S=π(R2-r2),据此先求出底面积,然后乘钢管的长度,即可得到这根钢管的体积,据此列式解答.
20.【答案】解:2÷2=1(米)
3.14×12×2
=3.14×2
=6.28(立方米)
6.28÷1.57=4(天)
答: 一个内底面直径和高都是2米的圆柱体水池装满水能浇4天。
【考点】圆柱的体积(容积)
【解析】【分析】根据题意可知,先求出这个圆柱体水池的容积,V=πr2h,据此列式计算;然后用水池的容积÷每天浇水的体积=可以浇水的天数,据此列式解答。
试题分析部分
1、试卷总体分布分析
总分:60分
分值分布 客观题(占比) 25.0(41.7%)
主观题(占比) 35.0(58.3%)
题量分布 客观题(占比) 15(75.0%)
主观题(占比) 5(25.0%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 5(25.0%) 5.0(8.3%)
解答题 3(15.0%) 15.0(25.0%)
计算题 2(10.0%) 20.0(33.3%)
单选题 5(25.0%) 10.0(16.7%)
判断题 5(25.0%) 10.0(16.7%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (100.0%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 圆柱的侧面积、表面积 16.0(26.7%) 2,3,6,8,13,14,15,18
2 圆锥的体积(容积) 10.0(16.7%) 1,7,12,17
3 圆柱的体积(容积) 46.0(76.7%) 1,2,4,7,8,9,10,11,12,16,17,19,20
4 组合体的体积的巧算 5.0(8.3%) 17
5 圆柱的特征 3.0(5.0%) 5,14
6 比的化简与求值 2.0(3.3%) 1
