2022年人教版小学数学六年级下册 第4单元正比例和反比例课后练(含答案)
文档属性
| 名称 | 2022年人教版小学数学六年级下册 第4单元正比例和反比例课后练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 87.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 06:50:14 | ||
图片预览




文档简介
2022年人教版小学数学六年级下册
第4单元 正比例和反比例 课后练
一、选择题 (将正确答案的字母填在括号里)
1.圆的面积与它的半径的平方( )。
A.不成比例 B.成反比例 C.成正比例
2.订阅《中国少年报》的份数与所付的报款( )
A.成正比例 B.成反比例 C.不成比例
3.表示x和y成正比例的关系式是( )
A.x+y=k(一定) B. =k
C. =k(一定) D.xy=k(一定)
4.下列各种关系中,成反比例关系的是( )。
A.某人年龄一定,他的身高与体重。
B.平行四边形的面积一定,它的底和高。
C.圆的面积一定,它的半径与圆周率。
D.三角形的高不变,它的底和面积。
5.下面两种相关联的量( )
正方体的棱长和它的体积.
A.成正比例 B.成反比例 C.不成比例
二、判断题 (对的在括号里打√,错的打 )
6.时间一定,路程和速度成反比例。( )
7.下面各题中的两个量是否成正比例。
(1)一袋大米,吃去的千克数与剩下的千克数。( )
(2)圆柱的高一定,它的体积和底面积。( )
(3)花生的出油率一定,花生的质量和榨出的油的质量。( )
(4)一个人的体重和年龄。( )
8.实际距离一定,图上距离与比例尺成正比例.( )
9.圆的周长一定,直径和圆周率成反比例。( )
10.小明应完成的作业量一定,他已完成的作业量和未完成的作业量成反比例。( )
三、填空题
11.下表中,如果a和b成正比例,则空缺处填 ;如果a和b成反比例,则空缺处填 。
a 8 6
b 12
12.自行车车轮转数与所行的路程成 比例。
13.有一批树苗,原计划30个人栽,每人要栽10棵,后来增加20人一起去栽,每人比原计划少栽 棵.(用比例解)
14.成语“立竿见影”用数学的眼光来看,这是应用了比例知识当中的 关系。
15.如果x= y,则x与y成 比例:如果y= ,则x与y成 比例。
四、计算题
16.修路队修一段路,头3天修了135米,照这样速度,又修了8天才修完这段路,这段路长多少米?
五、解答题
17.下面表中的两种量成什么比例?说明理由.
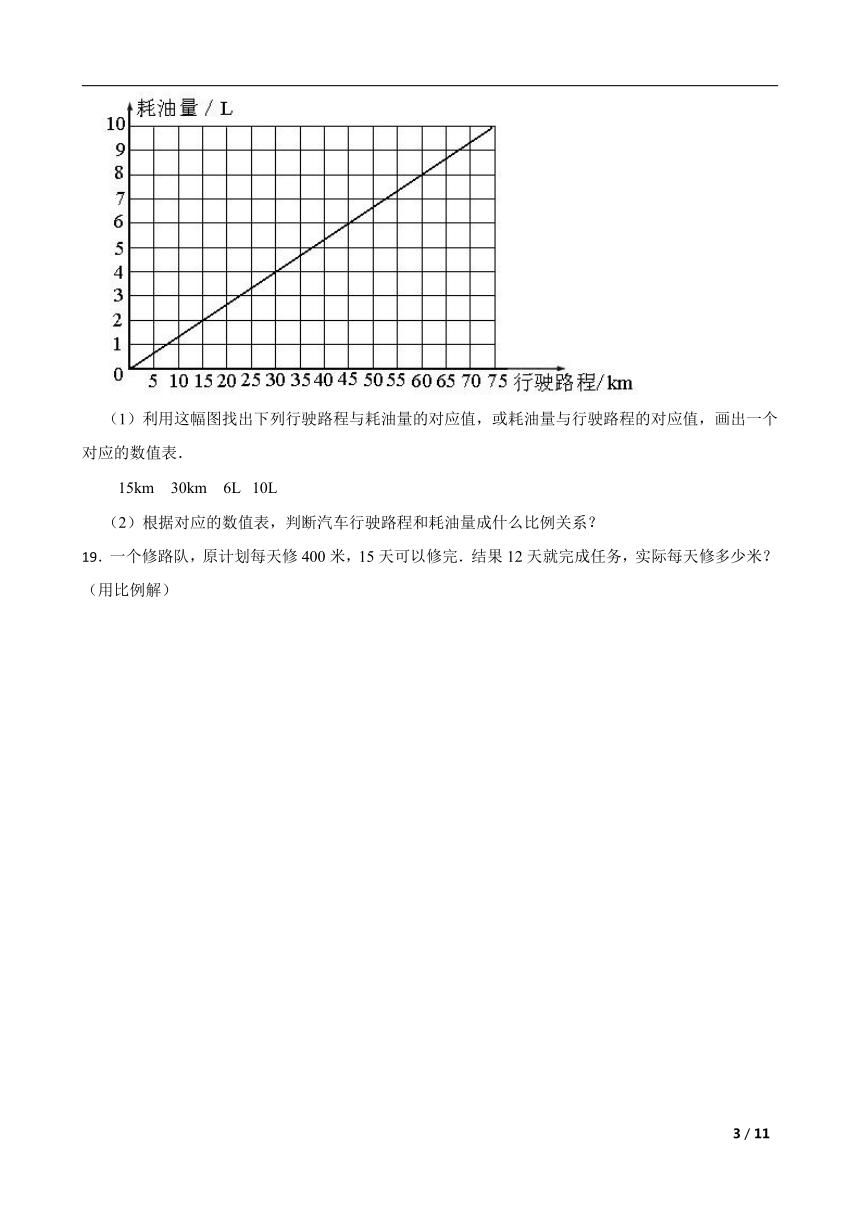
18.下面是某种汽车行驶路程和耗油量的图像.
(1)利用这幅图找出下列行驶路程与耗油量的对应值,或耗油量与行驶路程的对应值,画出一个对应的数值表.
15km 30km 6L 10L
(2)根据对应的数值表,判断汽车行驶路程和耗油量成什么比例关系?
19.一个修路队,原计划每天修400米,15天可以修完.结果12天就完成任务,实际每天修多少米?(用比例解)
答案解析部分
1.【答案】C
【考点】成正比例的量及其意义
【解析】【解答】解:圆的面积÷半径的平方=π(一定),二者成正比例.
故答案为:C
【分析】根据圆面积公式判断圆的面积和半径的平方的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例.
2.【答案】A
【考点】成正比例的量及其意义
【解析】【解答】解:因为 =每份《中国少年报》的价格(比值一定),
所以订阅《中国少年报》的份数与所付的报款成正比例;
故答案为:A.
【分析】由题意可知:每份少年报的单价一定,则订阅的份数与所付的报款成正比例.
3.【答案】C
【考点】成正比例的量及其意义
【解析】【解答】解:A、x+y=k(一定),是和一定;
B、 =k,是比值不一定;
C、 =k(一定),是比值一定;
D、xy=k(一定),是乘积一定。
【分析】成正比例关系的两种量,相对应的比值一定,由此做出判断。
故选:C
4.【答案】B
【考点】成反比例的量及其意义
【解析】【解答】选项A,某人年龄一定,他的身高与体重不成比例;
选项B,平行四边形的底×高=平行四边形的面积,当平行四边形的面积一定,它的底和高成反比例;
选项C,S=πr2, 当圆的面积一定时,圆周率也是一个定值,所以圆的面积一定,它的半径与圆周率不成比例;
选项D,三角形的面积÷底=高,当三角形的高不变,它的底和面积成正比例。
故答案为:B.
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,据此解答.
5.【答案】C
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】解:因为棱长3=正方体的体积,可知正方体体积÷棱长3=1(定值),所以正方体体积与棱长3成正比例,但正方体的棱长不确定,所以正方体体积÷棱长=棱长2(不确定),所以正方体的棱长和它的体积不成比例。
故选:C。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的商(比值)一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,本题中正方体的棱长不确定,所以正方体体积÷棱长=棱长2(不确定),正方体的棱长和它的体积的商不一定,据此即可解答此题。
6.【答案】(1)错误
【考点】成正比例的量及其意义
【解析】【解答】解:路程÷速度=时间,所以时间一定,路程和速度成正比例。
故答案为:错误
【分析】若y=(k为常数,x,y≠0),那么x和y成正比例。
7.【答案】解:①吃去的重量+剩下的重量=总重量,二者的和一定,不成正比例;②圆柱的体积÷底面积=高,高一定,圆柱的体积与底面积成正比例;③榨出油的质量÷花生的质量=出油率,出油率一定,花生的质量与榨出油的质量成正比例;④一个人的体重和年龄的比值不一定,不成正比例.
(1)错误
(2)正
(3)正
(4)错误
【考点】成正比例的量及其意义
【解析】【解答】解:①吃去的重量+剩下的重量=总重量,二者的和一定,不成正比例;
②圆柱的体积÷底面积=高,高一定,圆柱的体积与底面积成正比例;
③榨出油的质量÷花生的质量=出油率,出油率一定,花生的质量与榨出油的质量成正比例;
④一个人的体重和年龄的比值不一定,不成正比例.
【分析】判断两种量是不是成正比例,分三步:一是看它们是不是相关联的两种量;二是看一种量变化,另一种量是不是也随着变化,三是看两个量的比值是否一定.
8.【答案】(1)正
【考点】成正比例的量及其意义
【解析】【解答】解:图上距离÷比例尺=实际距离(一定),是比值一定,
所以图上距离和比例尺成正比例;
故答案为:正确.
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
9.【答案】(1)错误
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】圆周率是一个固定的数,跟直径不成比例。
故答案为:错误。
【分析】 判定两种相关联的量是否成正、反比例,不仅要看比值或乘积一定,还要看一种量是否随着另一种量的变化而变化,如果只是一种量变化,另一种量不变化,这两种相关联的量就不成正、反比例。
10.【答案】(1)错误
【考点】成反比例的量及其意义
【解析】【解答】解:小明应完成的作业量一定,他已完成的作业量和未完成的作业量不成比例。
故答案为:错误。
【分析】小明应完成的作业量=小明已经完成的作业量+未完成的作业量,不存在比例关系。
11.【答案】9;16
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】 下表中,如果a和b成正比例,12:8=1.5,6×1.5=9,则空缺处填9;如果a和b成反比例,8×12=96,96÷6=16,则空缺处填16。
a 8 6
b 12 16
故答案为:9;16。
【分析】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y:x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
12.【答案】正
【考点】成正比例的量及其意义
【解析】【解答】解:自行车车轮转数与所行的路程成正比例。
故答案为:正。
【分析】所行的路程÷自行车车轮转数=自行车车轮的周长(一定)。比值一定,成正比例。
13.【答案】4
【考点】反比例应用题
【解析】【解答】解:设每人比原计划少栽x棵.
10×30=(10-x)×(30+20)
10-x=6
x=4
故答案为:4
【分析】这批树苗的总数不变,每人栽的棵数与人数成反比例,设每人比原计划少栽x棵,则现在每人栽(10-x)棵,根据总棵数不变列出比例解答即可.
14.【答案】正比例
【考点】成正比例的量及其意义
【解析】【解答】成语“立竿见影”用数学的眼光来看,这是应用了比例知识当中的正比例关系。
故答案为:正比例
【分析】同一时间,同一地点,物体和它的影长的比值是固定不变的,成正比例关系。
15.【答案】正;反
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】解:由x= y得x÷y=,则x与y成正比例;
由y= 得xy=6,则x与y成反比例。
故答案为:正;反。
【分析】正比例的判断方法:相关联,能变化,商一定;反比例的判断方法:相关联,能变化,积一定。
16.【答案】解答:解:设这段路长x米。
3:135=(3+8):x,
3x=1885,
x=495。
答:这段路长495米。
【考点】正比例应用题
【解析】【分析】利用比例的意义和基本性质,每天修路的米数是一定的写出比例。本题考查利用比例的意义和基本性质写方程。此题要注意求全长。
17.【答案】解:7.8÷1=7.8(吨),39÷5=7.8(吨)
成正比例.因为钢铁的质量与钢铁的体积是一组相关联的量,钢铁的质量与体积的商一定,二者成正比例.
【考点】成正比例的量及其意义
【解析】【分析】先判断表格中的两个量是相关联的量,然后判断钢铁的质量与体积的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例,否则不成比例.
18.【答案】(1)解:利用这幅图找出行驶路程与耗油量的对应值:
行驶路程 耗油量
15Km 2L
30 Km 4L
45 Km 6L
75 Km 10L
(2)解:15÷2=7.5(km),30÷4=7.5(km),75÷10=7.5(km),行驶的路程与耗油量的商一定,行驶的路程与耗油量成正比例关系.
【考点】成正比例的量及其意义
【解析】【分析】(1)估计图像判断出各个耗油量对应的行驶的路程并画出一个表格;(2)计算对应的数据的商一定还是积一定,如果商一定,二者就成正比例,如果积一定二者就成反比例,否则不成比例.
19.【答案】解:实际每天修x米,
12x=400×15
12x=6000
x=500
答:实际每天修500米。
【考点】反比例应用题;应用比例解决实际问题
【解析】【分析】此题主要考查了用比例解决问题,根据题意可知,这条路的全长是不变的,设实际每天修x米,用实际每天修的米数×实际修的天数=计划每天修的米数×计划修的天数,据此列比例解答.
试题分析部分
1、试卷总体分布分析
总分:58分
分值分布 客观题(占比) 24.0(41.4%)
主观题(占比) 34.0(58.6%)
题量分布 客观题(占比) 13(68.4%)
主观题(占比) 6(31.6%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 5(26.3%) 7.0(12.1%)
解答题 3(15.8%) 20.0(34.5%)
计算题 1(5.3%) 5.0(8.6%)
单选题 5(26.3%) 10.0(17.2%)
判断题 5(26.3%) 16.0(27.6%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (100.0%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 成正比例的量及其意义 43.0(74.1%) 1,2,3,5,6,7,8,9,11,12,14,15,17,18
2 成反比例的量及其意义 12.0(20.7%) 4,5,9,10,11,15
3 反比例应用题 6.0(10.3%) 13,19
4 正比例应用题 5.0(8.6%) 16
5 应用比例解决实际问题 5.0(8.6%) 19
4 / 11
第4单元 正比例和反比例 课后练
一、选择题 (将正确答案的字母填在括号里)
1.圆的面积与它的半径的平方( )。
A.不成比例 B.成反比例 C.成正比例
2.订阅《中国少年报》的份数与所付的报款( )
A.成正比例 B.成反比例 C.不成比例
3.表示x和y成正比例的关系式是( )
A.x+y=k(一定) B. =k
C. =k(一定) D.xy=k(一定)
4.下列各种关系中,成反比例关系的是( )。
A.某人年龄一定,他的身高与体重。
B.平行四边形的面积一定,它的底和高。
C.圆的面积一定,它的半径与圆周率。
D.三角形的高不变,它的底和面积。
5.下面两种相关联的量( )
正方体的棱长和它的体积.
A.成正比例 B.成反比例 C.不成比例
二、判断题 (对的在括号里打√,错的打 )
6.时间一定,路程和速度成反比例。( )
7.下面各题中的两个量是否成正比例。
(1)一袋大米,吃去的千克数与剩下的千克数。( )
(2)圆柱的高一定,它的体积和底面积。( )
(3)花生的出油率一定,花生的质量和榨出的油的质量。( )
(4)一个人的体重和年龄。( )
8.实际距离一定,图上距离与比例尺成正比例.( )
9.圆的周长一定,直径和圆周率成反比例。( )
10.小明应完成的作业量一定,他已完成的作业量和未完成的作业量成反比例。( )
三、填空题
11.下表中,如果a和b成正比例,则空缺处填 ;如果a和b成反比例,则空缺处填 。
a 8 6
b 12
12.自行车车轮转数与所行的路程成 比例。
13.有一批树苗,原计划30个人栽,每人要栽10棵,后来增加20人一起去栽,每人比原计划少栽 棵.(用比例解)
14.成语“立竿见影”用数学的眼光来看,这是应用了比例知识当中的 关系。
15.如果x= y,则x与y成 比例:如果y= ,则x与y成 比例。
四、计算题
16.修路队修一段路,头3天修了135米,照这样速度,又修了8天才修完这段路,这段路长多少米?
五、解答题
17.下面表中的两种量成什么比例?说明理由.
18.下面是某种汽车行驶路程和耗油量的图像.
(1)利用这幅图找出下列行驶路程与耗油量的对应值,或耗油量与行驶路程的对应值,画出一个对应的数值表.
15km 30km 6L 10L
(2)根据对应的数值表,判断汽车行驶路程和耗油量成什么比例关系?
19.一个修路队,原计划每天修400米,15天可以修完.结果12天就完成任务,实际每天修多少米?(用比例解)
答案解析部分
1.【答案】C
【考点】成正比例的量及其意义
【解析】【解答】解:圆的面积÷半径的平方=π(一定),二者成正比例.
故答案为:C
【分析】根据圆面积公式判断圆的面积和半径的平方的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例.
2.【答案】A
【考点】成正比例的量及其意义
【解析】【解答】解:因为 =每份《中国少年报》的价格(比值一定),
所以订阅《中国少年报》的份数与所付的报款成正比例;
故答案为:A.
【分析】由题意可知:每份少年报的单价一定,则订阅的份数与所付的报款成正比例.
3.【答案】C
【考点】成正比例的量及其意义
【解析】【解答】解:A、x+y=k(一定),是和一定;
B、 =k,是比值不一定;
C、 =k(一定),是比值一定;
D、xy=k(一定),是乘积一定。
【分析】成正比例关系的两种量,相对应的比值一定,由此做出判断。
故选:C
4.【答案】B
【考点】成反比例的量及其意义
【解析】【解答】选项A,某人年龄一定,他的身高与体重不成比例;
选项B,平行四边形的底×高=平行四边形的面积,当平行四边形的面积一定,它的底和高成反比例;
选项C,S=πr2, 当圆的面积一定时,圆周率也是一个定值,所以圆的面积一定,它的半径与圆周率不成比例;
选项D,三角形的面积÷底=高,当三角形的高不变,它的底和面积成正比例。
故答案为:B.
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,据此解答.
5.【答案】C
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】解:因为棱长3=正方体的体积,可知正方体体积÷棱长3=1(定值),所以正方体体积与棱长3成正比例,但正方体的棱长不确定,所以正方体体积÷棱长=棱长2(不确定),所以正方体的棱长和它的体积不成比例。
故选:C。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的商(比值)一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,本题中正方体的棱长不确定,所以正方体体积÷棱长=棱长2(不确定),正方体的棱长和它的体积的商不一定,据此即可解答此题。
6.【答案】(1)错误
【考点】成正比例的量及其意义
【解析】【解答】解:路程÷速度=时间,所以时间一定,路程和速度成正比例。
故答案为:错误
【分析】若y=(k为常数,x,y≠0),那么x和y成正比例。
7.【答案】解:①吃去的重量+剩下的重量=总重量,二者的和一定,不成正比例;②圆柱的体积÷底面积=高,高一定,圆柱的体积与底面积成正比例;③榨出油的质量÷花生的质量=出油率,出油率一定,花生的质量与榨出油的质量成正比例;④一个人的体重和年龄的比值不一定,不成正比例.
(1)错误
(2)正
(3)正
(4)错误
【考点】成正比例的量及其意义
【解析】【解答】解:①吃去的重量+剩下的重量=总重量,二者的和一定,不成正比例;
②圆柱的体积÷底面积=高,高一定,圆柱的体积与底面积成正比例;
③榨出油的质量÷花生的质量=出油率,出油率一定,花生的质量与榨出油的质量成正比例;
④一个人的体重和年龄的比值不一定,不成正比例.
【分析】判断两种量是不是成正比例,分三步:一是看它们是不是相关联的两种量;二是看一种量变化,另一种量是不是也随着变化,三是看两个量的比值是否一定.
8.【答案】(1)正
【考点】成正比例的量及其意义
【解析】【解答】解:图上距离÷比例尺=实际距离(一定),是比值一定,
所以图上距离和比例尺成正比例;
故答案为:正确.
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
9.【答案】(1)错误
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】圆周率是一个固定的数,跟直径不成比例。
故答案为:错误。
【分析】 判定两种相关联的量是否成正、反比例,不仅要看比值或乘积一定,还要看一种量是否随着另一种量的变化而变化,如果只是一种量变化,另一种量不变化,这两种相关联的量就不成正、反比例。
10.【答案】(1)错误
【考点】成反比例的量及其意义
【解析】【解答】解:小明应完成的作业量一定,他已完成的作业量和未完成的作业量不成比例。
故答案为:错误。
【分析】小明应完成的作业量=小明已经完成的作业量+未完成的作业量,不存在比例关系。
11.【答案】9;16
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】 下表中,如果a和b成正比例,12:8=1.5,6×1.5=9,则空缺处填9;如果a和b成反比例,8×12=96,96÷6=16,则空缺处填16。
a 8 6
b 12 16
故答案为:9;16。
【分析】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y:x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
12.【答案】正
【考点】成正比例的量及其意义
【解析】【解答】解:自行车车轮转数与所行的路程成正比例。
故答案为:正。
【分析】所行的路程÷自行车车轮转数=自行车车轮的周长(一定)。比值一定,成正比例。
13.【答案】4
【考点】反比例应用题
【解析】【解答】解:设每人比原计划少栽x棵.
10×30=(10-x)×(30+20)
10-x=6
x=4
故答案为:4
【分析】这批树苗的总数不变,每人栽的棵数与人数成反比例,设每人比原计划少栽x棵,则现在每人栽(10-x)棵,根据总棵数不变列出比例解答即可.
14.【答案】正比例
【考点】成正比例的量及其意义
【解析】【解答】成语“立竿见影”用数学的眼光来看,这是应用了比例知识当中的正比例关系。
故答案为:正比例
【分析】同一时间,同一地点,物体和它的影长的比值是固定不变的,成正比例关系。
15.【答案】正;反
【考点】成正比例的量及其意义;成反比例的量及其意义
【解析】【解答】解:由x= y得x÷y=,则x与y成正比例;
由y= 得xy=6,则x与y成反比例。
故答案为:正;反。
【分析】正比例的判断方法:相关联,能变化,商一定;反比例的判断方法:相关联,能变化,积一定。
16.【答案】解答:解:设这段路长x米。
3:135=(3+8):x,
3x=1885,
x=495。
答:这段路长495米。
【考点】正比例应用题
【解析】【分析】利用比例的意义和基本性质,每天修路的米数是一定的写出比例。本题考查利用比例的意义和基本性质写方程。此题要注意求全长。
17.【答案】解:7.8÷1=7.8(吨),39÷5=7.8(吨)
成正比例.因为钢铁的质量与钢铁的体积是一组相关联的量,钢铁的质量与体积的商一定,二者成正比例.
【考点】成正比例的量及其意义
【解析】【分析】先判断表格中的两个量是相关联的量,然后判断钢铁的质量与体积的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例,否则不成比例.
18.【答案】(1)解:利用这幅图找出行驶路程与耗油量的对应值:
行驶路程 耗油量
15Km 2L
30 Km 4L
45 Km 6L
75 Km 10L
(2)解:15÷2=7.5(km),30÷4=7.5(km),75÷10=7.5(km),行驶的路程与耗油量的商一定,行驶的路程与耗油量成正比例关系.
【考点】成正比例的量及其意义
【解析】【分析】(1)估计图像判断出各个耗油量对应的行驶的路程并画出一个表格;(2)计算对应的数据的商一定还是积一定,如果商一定,二者就成正比例,如果积一定二者就成反比例,否则不成比例.
19.【答案】解:实际每天修x米,
12x=400×15
12x=6000
x=500
答:实际每天修500米。
【考点】反比例应用题;应用比例解决实际问题
【解析】【分析】此题主要考查了用比例解决问题,根据题意可知,这条路的全长是不变的,设实际每天修x米,用实际每天修的米数×实际修的天数=计划每天修的米数×计划修的天数,据此列比例解答.
试题分析部分
1、试卷总体分布分析
总分:58分
分值分布 客观题(占比) 24.0(41.4%)
主观题(占比) 34.0(58.6%)
题量分布 客观题(占比) 13(68.4%)
主观题(占比) 6(31.6%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 5(26.3%) 7.0(12.1%)
解答题 3(15.8%) 20.0(34.5%)
计算题 1(5.3%) 5.0(8.6%)
单选题 5(26.3%) 10.0(17.2%)
判断题 5(26.3%) 16.0(27.6%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (100.0%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 成正比例的量及其意义 43.0(74.1%) 1,2,3,5,6,7,8,9,11,12,14,15,17,18
2 成反比例的量及其意义 12.0(20.7%) 4,5,9,10,11,15
3 反比例应用题 6.0(10.3%) 13,19
4 正比例应用题 5.0(8.6%) 16
5 应用比例解决实际问题 5.0(8.6%) 19
4 / 11
