3.4函数的应用(一) 同步练习(Word版含解析)
文档属性
| 名称 | 3.4函数的应用(一) 同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 493.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 07:08:21 | ||
图片预览




文档简介
人教A版(2019)必修第一册 3.4 函数的应用(一)
一、单选题
1.2011年12月,某人的工资纳税额是元,若不考虑其他因素,则他该月工资收入为
级数 全月应纳税所得额 税率(%)
1 不超过元 3
2 元 10
注:本表所称全月应纳税所得额是以每月收入额减去(起征点)后的余额.A.7000元 B.7500元 C.6600元 D.5950元
2.一个矩形的周长是20,矩形的长y关于宽x的函数解析式为( )(默认y>x)
A.y=10-x(0B.y=10-2x(0C.y=20-x(0D.y=20-2x(03.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为,其中x代表拟录用人数,y代表面试人数,若面试人数为60,则该公司拟录用人数为( )
A.15 B.40 C.25 D.13
4.某厂日生产文具盒的总成本y(元)与日产量x(套)之间的关系为y=6x+30 000.而出厂价格为每套12元,要使该厂不亏本,至少日生产文具盒( )
A.2 000套 B.3 000套
C.4 000套 D.5 000套
5.某学校要召开学生代表大会,规定各班每10人推选一名代表 ,当各班人数除以10的余数大于6时再增选一名代表,那么,各班可推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为
A. B. C. D.
6.为定义在上周期为2的奇函数,则函数在上零点的个数最少为( )
A.5 B.6 C.11 D.12
7.某工厂近期要生产一批化工试剂,经市场调查得知,生产这批试剂的成本分为以下三个部分:①生产1单位试剂需要原料费50元;②支付所有职工的工资总额由7500元的基本工资和每生产1单位试剂补贴20元组成;③后续保养的费用是每单位元(试剂的总产量为单位,),则要使生产每单位试剂的成本最低,试剂总产量应为( )
A.60单位 B.70单位 C.80单位 D.90单位
8.某种图书,如果以每本2.5元的价格出售,可以售出8万本,若单价每提高0.1元,销售量将减少2000本,如果提价后的单价为元,下列各式中表示销售总收入不低于20万元的是
A. B.
C. D.
9.已知函数,若,则的取值范围为( )
A. B. C. D.
10.某商场对顾客实行购物优惠活动规定,一次购物付款总额:
(1)如果标价总额不超过200元,则不给予优惠;
(2)如果标价总额超过200元但不超过500元,则按标价总额给予9折优惠;
(3)如果标价总额超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予8折优惠.
某人两次去购物,分别付款180元和423元,假设他一次性购买上述两次同样的商品,则应付款( )
A.550元 B.560元 C.570元 D.580元
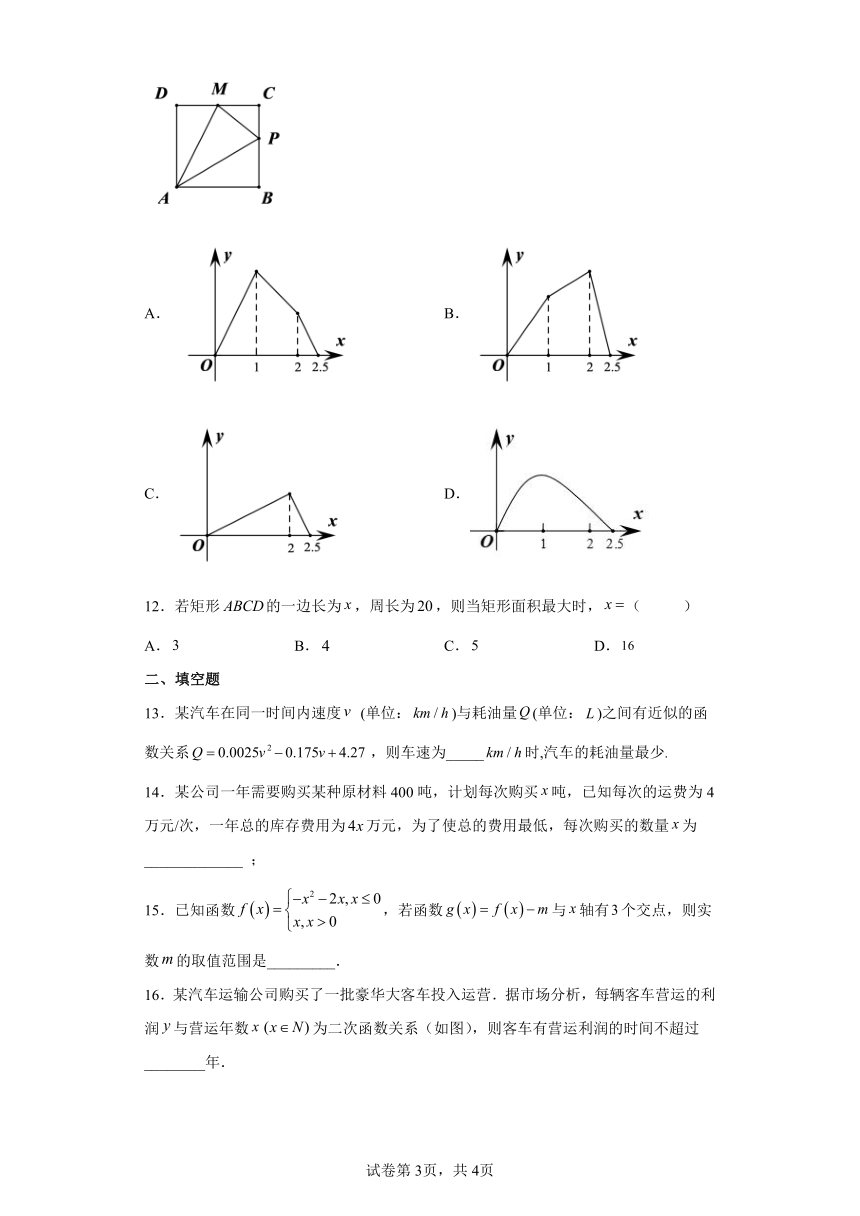
11.如图,点在边长为1的正方形的边上运动,是的中点,则当沿运动时,点经过的路程与的面积的函数的图象大致是下图中的
A. B.
C. D.
12.若矩形的一边长为,周长为,则当矩形面积最大时,( )
A. B. C. D.
二、填空题
13.某汽车在同一时间内速度 (单位:)与耗油量(单位:)之间有近似的函数关系,则车速为_____时,汽车的耗油量最少.
14.某公司一年需要购买某种原材料400吨,计划每次购买吨,已知每次的运费为4万元/次,一年总的库存费用为万元,为了使总的费用最低,每次购买的数量为 _____________ ;
15.已知函数,若函数与轴有个交点,则实数的取值范围是_________.
16.某汽车运输公司购买了一批豪华大客车投入运营.据市场分析,每辆客车营运的利润与营运年数为二次函数关系(如图),则客车有营运利润的时间不超过________年.
17.某企业开发一种产品,生产这种产品的年固定成本为3600万元,每生产x千件,需投入成本c(x)万元,c(x)=x2+10x.若该产品每千件定价a万元,为保证生产该产品不亏损,则a的最小值为_____.
三、解答题
18.某广告公司要为客户设计一幅周长为l(单位:m)的矩形广告牌,如何设计这个广告牌可以使广告牌的面积最大?
19.某商店试销一种成本单价为40元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量(件)与销售单价(元/件)可近似看作一次函数的关系.设商店获得的利润(利润销售总收入总成本)为元.
(1)试用销售单价表示利润;
(2)试问销售单价定为多少时,该商店可获得最大利润?最大利润是多少?此时的销售量是多少?
20.某地发生地质灾害,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质.已知每投放质量为m的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足,其中,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于4(毫克/升) 且不高于10(毫克/升)时称为最佳净化.
(1)如果投放的药剂质量为m=4,试问自来水达到有效净化一共可持续几天?
(2)如果投放的药剂质量为m,为了使在7天(从投放药剂算起包括7天)之内的自来水达到最佳净化,试确定应该投放的药剂质量m的最小值.
21.试用描点法画出函数的图象,求函数的定义域、值域;讨论函数的单调性、奇偶性,并证明.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
设此人的工资为元,则根据题设条件可得纳税额与的关系,再令,则可得此人的工资收入.
【详解】
设此人的工资为元,纳税额为,则有,
当时,,故当(元)时,,
令,
则(元),故选A.
本题考查分段函数的应用,属于基础题.
2.A
利用周长列方程,化简求得关于的表达式,求得定义域,由此求得函数解析式.
【详解】
由题意可知2y+2x=20,即y=10-x,又10-x>x,所以0所以函数解析式为.
故选:A
3.C
这是已知函数值求自变量的问题,又是分段函数,所以分类讨论求解即可.
【详解】
解:令,若,则,不合题意;
若,则,满足题意;
若,则,不合题意.
故拟录用人数为25.
故选:.
本题考查的是分段函数问题,在解答的过程当中充分体现了应用题的特性、分段函数的知识以及问题转化的思想,属于基础题.
4.D
列出利润的表达式再求解的解即可.
【详解】
因利润z=12x-(6x+30 000),所以z=6x-30 000,由z≥0解得x≥5 000,故至少日生产文具盒5 000套.
故选:D
本题主要考查了实际应用中的利润问题,属于基础题.
5.B
【详解】
试题分析:根据规定每人推选一名代表,当各班人数除以的余数大于时增加一名代表,即余数分别为时可以增选一名代表,也就是要进一位,所以最小应该加,因此利用取整函数可表示为,也可以用特殊取值法,若,排除C,D,若,排除A,故选B.
考点:函数的解析式及常用方法.
【方法点晴】本题主要考查了函数的解析式问题,其中解答中涉及到取整函数的概念,函数解析式的求解等知识点的考查,着重考查了学生分析问题和解答问题的能力,此类问题的解答中主要是读懂题意,在根据数学知识即可得到答案,对于选择题要选择最恰当的方法,试题有一定的难度,属于中档试题.
6.C
由奇函数的性质及函数的周期性即可得方程的解,即可得解.
【详解】
因为为定义在上周期为2的奇函数,
所以,,
所以,,,,
所以,
所以,即,
所以,,,,.
所以函数在上零点的个数为11.
故选:C.
本题考查了函数奇偶性与周期性的应用,考查了函数零点的概念,属于基础题.
7.D
设生产每单位试剂的成本为,求出原料总费用,职工的工资总额,后续保养总费用,从而表示出,然后利用基本不等式求解最值即可.
【详解】
解:设每生产单位试剂的成本为,
因为试剂总产量为单位,则由题意可知,原料总费用为元,
职工的工资总额为元,后续保养总费用为元,
则,
当且仅当,即时取等号,
满足,
所以要使生产每单位试剂的成本最低,试剂总产量应为90单位.
故选:D.
8.C
利用每本提高钱数乘以实际售出为总收入列不等式即可
【详解】
提价后的价格为元,则提高了元,则销售减少了本,即减少了万本,实际售出万本,则总收入为,
故选C
本题考查二次函数的实际应用问题,准确分析题意是关键,是基础题
9.B
根据分段函数的单调性以及,可得且,令,则,然后用表示,再作差,构造函数,并利用单调性可求得结果.
【详解】
因为函数在上递减,在上递增,又,
所以,且,令,则,
所以,,
所以,
设函数,,
∵在上单调递增,
∴,即,
∴,
故选:B.
关键点点睛:根据分段函数的单调性以及得到,且是解题关键.属于中档题.
10.C
先判断第一次购物不超过200,第二次不超过500,计算得到共购物650元,再计算得到答案.
【详解】
若第一次购物超过200,则付款大于,故第一次购物不超过200元;
若第二次购物超过500,则付款大于,故第二次购物不超过500元;
第二次购物 合计
付款为
故选:
本题考查了分段函数的应用,意在考查学生的计算能力和应用能力.
11.A
先分点在上时,点在上时,点在上时求得函数,再利用函数的性质来判断.
【详解】
当点在上时:
当点在上时:
当点在上时:
由函数可知,有三段直线,又当点在上时是减函数
故选:A
本题主要考查了分段函数的图象和性质,还考查了运算求解的能力,属于中档题.
12.C
求出矩形的面积关于的函数表达式,利用二次函数的基本性质可求得矩形面积的最值及其对应的值.
【详解】
矩形另一边长为,且有,
面积为,所以,当时,取最大值.
故选:C.
本题考查二次函数模型的应用,涉及二次函数最值的求解,考查计算能力,属于中等题.
13.35
利用二次函数的性质可求耗油量最少时对应的的值.
【详解】
因为可化简
,故当时,汽车的耗油量最少.
故填.
本题考查二次函数在实际问题中的应用,属于基础题.
14.20吨
依题意写出表达式,均值不等式求最小值.
【详解】
由题意,总的费用,当时取“=”,所以答案为20吨.
实际问题一定注意实际问题中自变量的取值,取等号的条件.
15.
先将函数与轴有个交点,转化成与的交点问题,再作出分段函数的图像,利用数形结合求得范围即可.
【详解】
依题意,函数与轴有个交点, 即与有3个交点,
作分段函数的图像如下,
由图可知,的取值范围为.
故答案为:.
方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图像,利用数形结合的方法求解.
16.7
确定函数解析式,解不等式,即可得到结论.
【详解】
设二次函数y=a(x-6)2+11,
又过点(4,7),
所以a=-1,即y=-(x-6)2+11.
解y≥0,得6-≤x≤6+,
所以有营运利润的时间为2.
又6<2<7,所以有营运利润的时间不超过7年.
故答案为:7
17.130
本题先根据题意建立函数与不等式关系,再运用参变分离化简,最后运用基本不等式求最值即可.
【详解】
解:有题意建立利润函数关系:,()
整理得:,
为保证生产该产品不亏损,则,()
即,
当且仅当即,取最小值130,此时产品不亏损
故答案为:130.
本题考查函数与不等式关系、参变分离法,基本不等式解决实际问题中的最值问题,是基础题.
18.边长为的正方形时
设广告牌的长为,则宽为,根据矩形的面积公式配方即可求解.
【详解】
解:设广告牌的长为,则宽为.
设广告牌的面积为.则.
当时,y取最大值.此时宽为.
∴当这个广告牌为边长为的正方形时,面积最大.
本题考查了二次函数模型的应用,注意定义域的取值范围,属于基础题.
19.(1);(2)当销售单价为70元/件时,可获得最大利润900元,此时销售量是30件.
(1)由利润销售总收入总成本可得答案;
(2)对于配方法即可求得最大值.
【详解】
(1)
.
(2),
∴当销售单价为70元/件时,可获得最大利润900元,此时销售量是30件.
20.(1)16天(2)
(1)由题意首先得到该药剂在水中释放的浓度的解析式,然后求解不等式即可确定自来水达到有效净化一共可持续的天数.
(2)由确定各段的单调性,求出值域,然后将原问题转化为恒成立的问题可得m的最小值.
【详解】
(1)由题意,当药剂质量为m=4,所以
当时,显然符合题意.
当x>4时,解得,
综上,
所以自来水达到有效净化一共可持续16天.
(2)由,得:
在区间(0,4]上单调递增,即;
在区间(4,7]上单调递减,即,
综上,
为使恒成立,只要且即可,
即所以应该投放的药剂质量m的最小值为
本题考查分段函数的应用,考查函数的单调性及应用:求值域,注意函数的各段解析式,属于中档题.
21.图像见解析,定义域:,值域:,讨论见解析,证明见解析
函数,可得.可得定义域,,可得,可得值域;在求解奇偶性,并作出其大致图象,利用定义证明单调性即可;
【详解】
解:.
列表:
x … -3 -2 -1 1 2 3 …
… 1 1 …
描点,连线.图象如图所示.
定义域:,值域:.在上是增函数,在上是减函数.
证明如下:设任意的,且.则.
.
,即,在上是增函数.
设任意的,且,则.
,
,即.
在上是减函数.
是偶函数.
本题考查幂函数的图象及性质,单调性的证明,属于中档题.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.2011年12月,某人的工资纳税额是元,若不考虑其他因素,则他该月工资收入为
级数 全月应纳税所得额 税率(%)
1 不超过元 3
2 元 10
注:本表所称全月应纳税所得额是以每月收入额减去(起征点)后的余额.A.7000元 B.7500元 C.6600元 D.5950元
2.一个矩形的周长是20,矩形的长y关于宽x的函数解析式为( )(默认y>x)
A.y=10-x(0
A.15 B.40 C.25 D.13
4.某厂日生产文具盒的总成本y(元)与日产量x(套)之间的关系为y=6x+30 000.而出厂价格为每套12元,要使该厂不亏本,至少日生产文具盒( )
A.2 000套 B.3 000套
C.4 000套 D.5 000套
5.某学校要召开学生代表大会,规定各班每10人推选一名代表 ,当各班人数除以10的余数大于6时再增选一名代表,那么,各班可推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为
A. B. C. D.
6.为定义在上周期为2的奇函数,则函数在上零点的个数最少为( )
A.5 B.6 C.11 D.12
7.某工厂近期要生产一批化工试剂,经市场调查得知,生产这批试剂的成本分为以下三个部分:①生产1单位试剂需要原料费50元;②支付所有职工的工资总额由7500元的基本工资和每生产1单位试剂补贴20元组成;③后续保养的费用是每单位元(试剂的总产量为单位,),则要使生产每单位试剂的成本最低,试剂总产量应为( )
A.60单位 B.70单位 C.80单位 D.90单位
8.某种图书,如果以每本2.5元的价格出售,可以售出8万本,若单价每提高0.1元,销售量将减少2000本,如果提价后的单价为元,下列各式中表示销售总收入不低于20万元的是
A. B.
C. D.
9.已知函数,若,则的取值范围为( )
A. B. C. D.
10.某商场对顾客实行购物优惠活动规定,一次购物付款总额:
(1)如果标价总额不超过200元,则不给予优惠;
(2)如果标价总额超过200元但不超过500元,则按标价总额给予9折优惠;
(3)如果标价总额超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予8折优惠.
某人两次去购物,分别付款180元和423元,假设他一次性购买上述两次同样的商品,则应付款( )
A.550元 B.560元 C.570元 D.580元
11.如图,点在边长为1的正方形的边上运动,是的中点,则当沿运动时,点经过的路程与的面积的函数的图象大致是下图中的
A. B.
C. D.
12.若矩形的一边长为,周长为,则当矩形面积最大时,( )
A. B. C. D.
二、填空题
13.某汽车在同一时间内速度 (单位:)与耗油量(单位:)之间有近似的函数关系,则车速为_____时,汽车的耗油量最少.
14.某公司一年需要购买某种原材料400吨,计划每次购买吨,已知每次的运费为4万元/次,一年总的库存费用为万元,为了使总的费用最低,每次购买的数量为 _____________ ;
15.已知函数,若函数与轴有个交点,则实数的取值范围是_________.
16.某汽车运输公司购买了一批豪华大客车投入运营.据市场分析,每辆客车营运的利润与营运年数为二次函数关系(如图),则客车有营运利润的时间不超过________年.
17.某企业开发一种产品,生产这种产品的年固定成本为3600万元,每生产x千件,需投入成本c(x)万元,c(x)=x2+10x.若该产品每千件定价a万元,为保证生产该产品不亏损,则a的最小值为_____.
三、解答题
18.某广告公司要为客户设计一幅周长为l(单位:m)的矩形广告牌,如何设计这个广告牌可以使广告牌的面积最大?
19.某商店试销一种成本单价为40元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量(件)与销售单价(元/件)可近似看作一次函数的关系.设商店获得的利润(利润销售总收入总成本)为元.
(1)试用销售单价表示利润;
(2)试问销售单价定为多少时,该商店可获得最大利润?最大利润是多少?此时的销售量是多少?
20.某地发生地质灾害,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质.已知每投放质量为m的药剂后,经过x天该药剂在水中释放的浓度y(毫克/升)满足,其中,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于4(毫克/升) 且不高于10(毫克/升)时称为最佳净化.
(1)如果投放的药剂质量为m=4,试问自来水达到有效净化一共可持续几天?
(2)如果投放的药剂质量为m,为了使在7天(从投放药剂算起包括7天)之内的自来水达到最佳净化,试确定应该投放的药剂质量m的最小值.
21.试用描点法画出函数的图象,求函数的定义域、值域;讨论函数的单调性、奇偶性,并证明.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
设此人的工资为元,则根据题设条件可得纳税额与的关系,再令,则可得此人的工资收入.
【详解】
设此人的工资为元,纳税额为,则有,
当时,,故当(元)时,,
令,
则(元),故选A.
本题考查分段函数的应用,属于基础题.
2.A
利用周长列方程,化简求得关于的表达式,求得定义域,由此求得函数解析式.
【详解】
由题意可知2y+2x=20,即y=10-x,又10-x>x,所以0
故选:A
3.C
这是已知函数值求自变量的问题,又是分段函数,所以分类讨论求解即可.
【详解】
解:令,若,则,不合题意;
若,则,满足题意;
若,则,不合题意.
故拟录用人数为25.
故选:.
本题考查的是分段函数问题,在解答的过程当中充分体现了应用题的特性、分段函数的知识以及问题转化的思想,属于基础题.
4.D
列出利润的表达式再求解的解即可.
【详解】
因利润z=12x-(6x+30 000),所以z=6x-30 000,由z≥0解得x≥5 000,故至少日生产文具盒5 000套.
故选:D
本题主要考查了实际应用中的利润问题,属于基础题.
5.B
【详解】
试题分析:根据规定每人推选一名代表,当各班人数除以的余数大于时增加一名代表,即余数分别为时可以增选一名代表,也就是要进一位,所以最小应该加,因此利用取整函数可表示为,也可以用特殊取值法,若,排除C,D,若,排除A,故选B.
考点:函数的解析式及常用方法.
【方法点晴】本题主要考查了函数的解析式问题,其中解答中涉及到取整函数的概念,函数解析式的求解等知识点的考查,着重考查了学生分析问题和解答问题的能力,此类问题的解答中主要是读懂题意,在根据数学知识即可得到答案,对于选择题要选择最恰当的方法,试题有一定的难度,属于中档试题.
6.C
由奇函数的性质及函数的周期性即可得方程的解,即可得解.
【详解】
因为为定义在上周期为2的奇函数,
所以,,
所以,,,,
所以,
所以,即,
所以,,,,.
所以函数在上零点的个数为11.
故选:C.
本题考查了函数奇偶性与周期性的应用,考查了函数零点的概念,属于基础题.
7.D
设生产每单位试剂的成本为,求出原料总费用,职工的工资总额,后续保养总费用,从而表示出,然后利用基本不等式求解最值即可.
【详解】
解:设每生产单位试剂的成本为,
因为试剂总产量为单位,则由题意可知,原料总费用为元,
职工的工资总额为元,后续保养总费用为元,
则,
当且仅当,即时取等号,
满足,
所以要使生产每单位试剂的成本最低,试剂总产量应为90单位.
故选:D.
8.C
利用每本提高钱数乘以实际售出为总收入列不等式即可
【详解】
提价后的价格为元,则提高了元,则销售减少了本,即减少了万本,实际售出万本,则总收入为,
故选C
本题考查二次函数的实际应用问题,准确分析题意是关键,是基础题
9.B
根据分段函数的单调性以及,可得且,令,则,然后用表示,再作差,构造函数,并利用单调性可求得结果.
【详解】
因为函数在上递减,在上递增,又,
所以,且,令,则,
所以,,
所以,
设函数,,
∵在上单调递增,
∴,即,
∴,
故选:B.
关键点点睛:根据分段函数的单调性以及得到,且是解题关键.属于中档题.
10.C
先判断第一次购物不超过200,第二次不超过500,计算得到共购物650元,再计算得到答案.
【详解】
若第一次购物超过200,则付款大于,故第一次购物不超过200元;
若第二次购物超过500,则付款大于,故第二次购物不超过500元;
第二次购物 合计
付款为
故选:
本题考查了分段函数的应用,意在考查学生的计算能力和应用能力.
11.A
先分点在上时,点在上时,点在上时求得函数,再利用函数的性质来判断.
【详解】
当点在上时:
当点在上时:
当点在上时:
由函数可知,有三段直线,又当点在上时是减函数
故选:A
本题主要考查了分段函数的图象和性质,还考查了运算求解的能力,属于中档题.
12.C
求出矩形的面积关于的函数表达式,利用二次函数的基本性质可求得矩形面积的最值及其对应的值.
【详解】
矩形另一边长为,且有,
面积为,所以,当时,取最大值.
故选:C.
本题考查二次函数模型的应用,涉及二次函数最值的求解,考查计算能力,属于中等题.
13.35
利用二次函数的性质可求耗油量最少时对应的的值.
【详解】
因为可化简
,故当时,汽车的耗油量最少.
故填.
本题考查二次函数在实际问题中的应用,属于基础题.
14.20吨
依题意写出表达式,均值不等式求最小值.
【详解】
由题意,总的费用,当时取“=”,所以答案为20吨.
实际问题一定注意实际问题中自变量的取值,取等号的条件.
15.
先将函数与轴有个交点,转化成与的交点问题,再作出分段函数的图像,利用数形结合求得范围即可.
【详解】
依题意,函数与轴有个交点, 即与有3个交点,
作分段函数的图像如下,
由图可知,的取值范围为.
故答案为:.
方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图像,利用数形结合的方法求解.
16.7
确定函数解析式,解不等式,即可得到结论.
【详解】
设二次函数y=a(x-6)2+11,
又过点(4,7),
所以a=-1,即y=-(x-6)2+11.
解y≥0,得6-≤x≤6+,
所以有营运利润的时间为2.
又6<2<7,所以有营运利润的时间不超过7年.
故答案为:7
17.130
本题先根据题意建立函数与不等式关系,再运用参变分离化简,最后运用基本不等式求最值即可.
【详解】
解:有题意建立利润函数关系:,()
整理得:,
为保证生产该产品不亏损,则,()
即,
当且仅当即,取最小值130,此时产品不亏损
故答案为:130.
本题考查函数与不等式关系、参变分离法,基本不等式解决实际问题中的最值问题,是基础题.
18.边长为的正方形时
设广告牌的长为,则宽为,根据矩形的面积公式配方即可求解.
【详解】
解:设广告牌的长为,则宽为.
设广告牌的面积为.则.
当时,y取最大值.此时宽为.
∴当这个广告牌为边长为的正方形时,面积最大.
本题考查了二次函数模型的应用,注意定义域的取值范围,属于基础题.
19.(1);(2)当销售单价为70元/件时,可获得最大利润900元,此时销售量是30件.
(1)由利润销售总收入总成本可得答案;
(2)对于配方法即可求得最大值.
【详解】
(1)
.
(2),
∴当销售单价为70元/件时,可获得最大利润900元,此时销售量是30件.
20.(1)16天(2)
(1)由题意首先得到该药剂在水中释放的浓度的解析式,然后求解不等式即可确定自来水达到有效净化一共可持续的天数.
(2)由确定各段的单调性,求出值域,然后将原问题转化为恒成立的问题可得m的最小值.
【详解】
(1)由题意,当药剂质量为m=4,所以
当时,显然符合题意.
当x>4时,解得,
综上,
所以自来水达到有效净化一共可持续16天.
(2)由,得:
在区间(0,4]上单调递增,即;
在区间(4,7]上单调递减,即,
综上,
为使恒成立,只要且即可,
即所以应该投放的药剂质量m的最小值为
本题考查分段函数的应用,考查函数的单调性及应用:求值域,注意函数的各段解析式,属于中档题.
21.图像见解析,定义域:,值域:,讨论见解析,证明见解析
函数,可得.可得定义域,,可得,可得值域;在求解奇偶性,并作出其大致图象,利用定义证明单调性即可;
【详解】
解:.
列表:
x … -3 -2 -1 1 2 3 …
… 1 1 …
描点,连线.图象如图所示.
定义域:,值域:.在上是增函数,在上是减函数.
证明如下:设任意的,且.则.
.
,即,在上是增函数.
设任意的,且,则.
,
,即.
在上是减函数.
是偶函数.
本题考查幂函数的图象及性质,单调性的证明,属于中档题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
