人教版数学八年级下册17.2勾股定理的逆定理课件
文档属性
| 名称 | 人教版数学八年级下册17.2勾股定理的逆定理课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 09:43:52 | ||
图片预览




文档简介
(共16张PPT)
17.2.1
勾股定理的逆定理
1.直角三角形有哪些性质
2.如何判断三角形是直角三角形
一、复习回顾
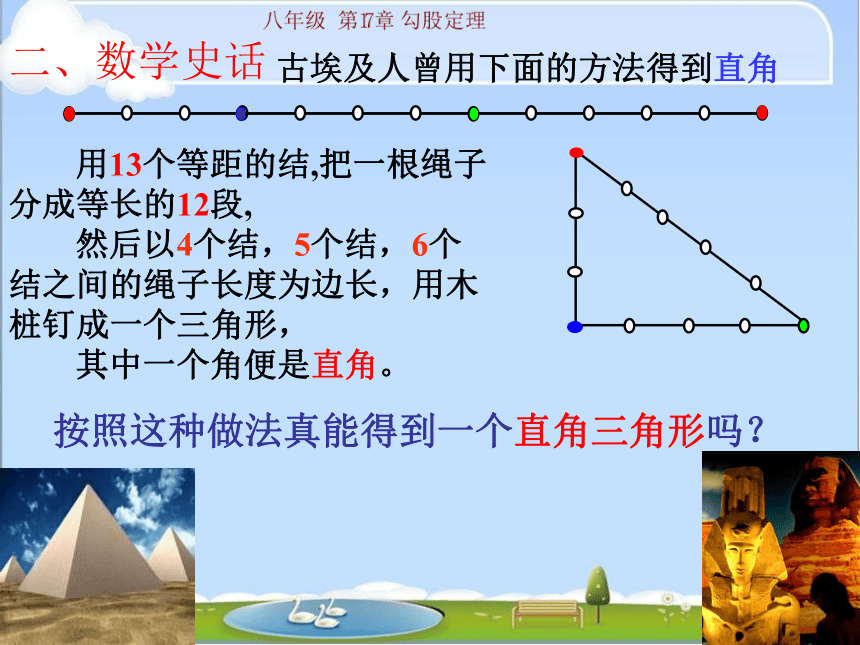
古埃及人曾用下面的方法得到直角
二、数学史话
按照这种做法真能得到一个直角三角形吗?
用13个等距的结,把一根绳子分成等长的12段,
然后以4个结,5个结,6个结之间的绳子长度为边长,用木桩钉成一个三角形,
其中一个角便是直角。
3
4
5
请同学们观察,这个三角形的三条边有什么关系吗
3
2
4
2
5
2
+
=
三、观察与思考
a,b,c分别是一个三角形的三边长6,8,10
(1)这三个数满足
吗?
(2)这个三角形是直角三角形吗?
类比研究
由上面例子你发现了什么结论
请以命题的形式说出你的观点!
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
a2 + b2 = c2
讨论
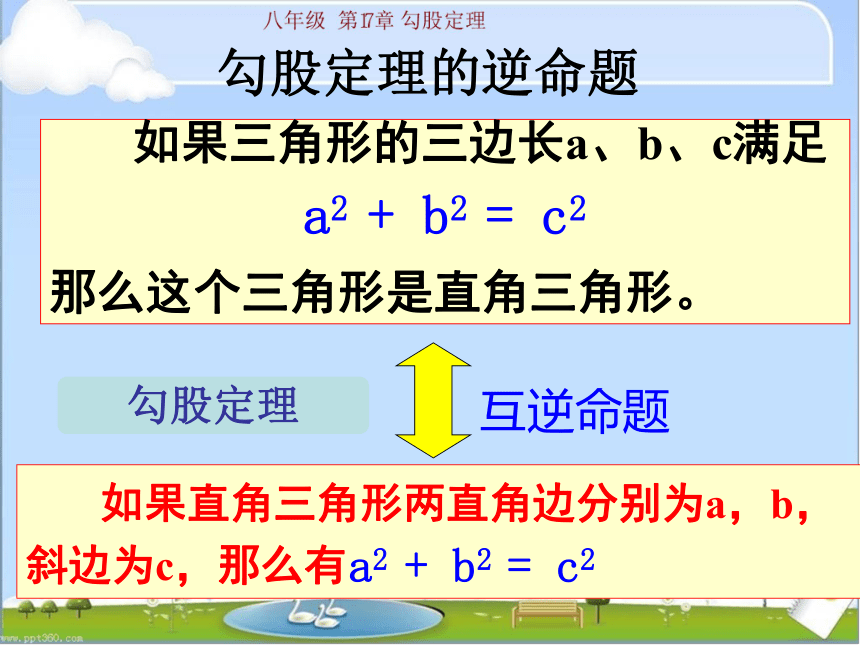
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么有
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
a2 + b2 = c2
互逆命题
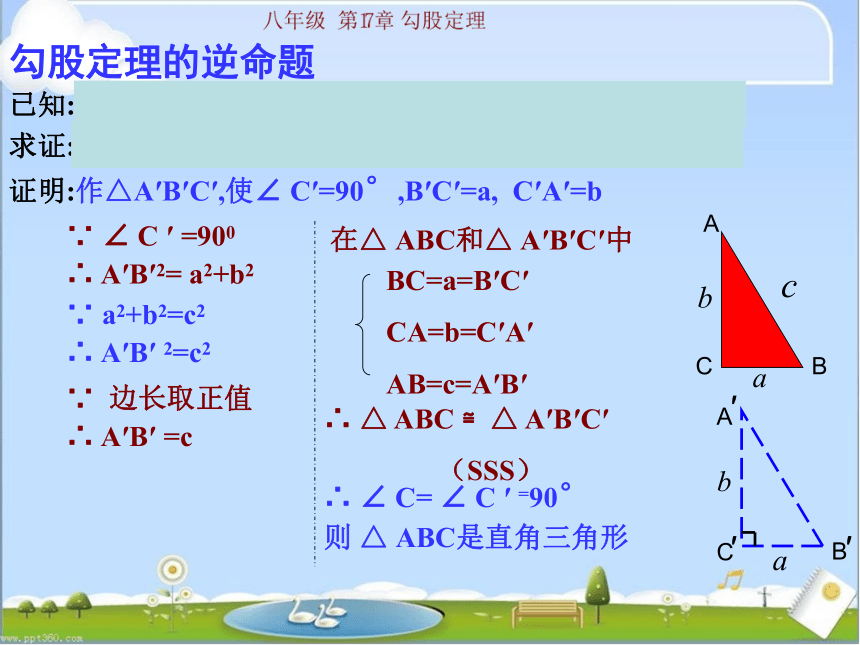
已知:在△ABC中,AB=c ,BC=a ,CA=b ,且a2+b2=c2。
求证:△ ABC是直角三角形
A
C
B
A
′
B
′
C
′
勾股定理的逆命题
证明:作△A′B′C′,使∠ C′=90°,B′C′=a, C′A′=b
∵ ∠ C ′ =900
∴ A′B′2= a2+b2
∵ a2+b2=c2
∴ A′B′ 2=c2
∵ 边长取正值
∴ A′B′ =c
∴ △ ABC ≌△ A′B′C′
(SSS)
∴ ∠ C= ∠ C ′ =90°
BC=a=B′C′
CA=b=C′A′
AB=c=A′B′
在△ ABC和△ A′B′C′中
则 △ ABC是直角三角形
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。(且边C所对的角为直角。)
a2 + b2 = c2
互逆命题
逆定理
定理
我们已经学习了一些互逆的定理,如:
1.勾股定理及其逆定理;
2.两直线平行,内错角相等; 内错角相等,两直线平行.
3.角的平分线的性质与判定;
4.线段的垂直平分线的性质与判定。
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
四、定理与逆定理
说出下列命题的逆命题.并判断这些命题的逆命题成立吗
说一说,练一练
(1) 如果两个实数相等,那么它们的平方相等.
(2) 对顶角相等.
逆命题:如果两个实数的平方相等,那么这两个实数相等. 不成立
逆命题:如果两个角相等,那么这两个角是对顶角. 不成立
感悟: 原命题成立时, 逆命题有时成立, 有时不成立
一个命题是真命题,它逆命题却不一定是真命题.
例1 判断由a、b、c的边长组成的三角形是不是直角三角形:(1) a=15 , b =8 , c=17
(2) a=13 , b =15 , c=14
分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。
五、例题讲解
练习:下面以a,b,c为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) a=25,b=20,c=15 ____ _____ ;
(2) a=13,b=13,c=15 ____ _____ ;
是
不是
∠ A=900
像25,20,15或者15,8,17这样,能够成为直角三角形三条边长的三个正整数,称为勾股数.
1.请你说出常用的勾股数;
2.一组勾股数的正整数倍一定是勾股数吗?为什么
挑战自我
例2:已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积
A
B
C
D
中考链接
例3: “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
A
B
O
E
N
远航
海天
海天
如图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD,求证:∠AEF=90 .
A
F
E
C
B
D
六、拓展思考
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
七、小结
八、作业
《新观察》P27-28
17.2.1
勾股定理的逆定理
1.直角三角形有哪些性质
2.如何判断三角形是直角三角形
一、复习回顾
古埃及人曾用下面的方法得到直角
二、数学史话
按照这种做法真能得到一个直角三角形吗?
用13个等距的结,把一根绳子分成等长的12段,
然后以4个结,5个结,6个结之间的绳子长度为边长,用木桩钉成一个三角形,
其中一个角便是直角。
3
4
5
请同学们观察,这个三角形的三条边有什么关系吗
3
2
4
2
5
2
+
=
三、观察与思考
a,b,c分别是一个三角形的三边长6,8,10
(1)这三个数满足
吗?
(2)这个三角形是直角三角形吗?
类比研究
由上面例子你发现了什么结论
请以命题的形式说出你的观点!
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
a2 + b2 = c2
讨论
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么有
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。
a2 + b2 = c2
互逆命题
已知:在△ABC中,AB=c ,BC=a ,CA=b ,且a2+b2=c2。
求证:△ ABC是直角三角形
A
C
B
A
′
B
′
C
′
勾股定理的逆命题
证明:作△A′B′C′,使∠ C′=90°,B′C′=a, C′A′=b
∵ ∠ C ′ =900
∴ A′B′2= a2+b2
∵ a2+b2=c2
∴ A′B′ 2=c2
∵ 边长取正值
∴ A′B′ =c
∴ △ ABC ≌△ A′B′C′
(SSS)
∴ ∠ C= ∠ C ′ =90°
BC=a=B′C′
CA=b=C′A′
AB=c=A′B′
在△ ABC和△ A′B′C′中
则 △ ABC是直角三角形
勾股定理的逆命题
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形。(且边C所对的角为直角。)
a2 + b2 = c2
互逆命题
逆定理
定理
我们已经学习了一些互逆的定理,如:
1.勾股定理及其逆定理;
2.两直线平行,内错角相等; 内错角相等,两直线平行.
3.角的平分线的性质与判定;
4.线段的垂直平分线的性质与判定。
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
四、定理与逆定理
说出下列命题的逆命题.并判断这些命题的逆命题成立吗
说一说,练一练
(1) 如果两个实数相等,那么它们的平方相等.
(2) 对顶角相等.
逆命题:如果两个实数的平方相等,那么这两个实数相等. 不成立
逆命题:如果两个角相等,那么这两个角是对顶角. 不成立
感悟: 原命题成立时, 逆命题有时成立, 有时不成立
一个命题是真命题,它逆命题却不一定是真命题.
例1 判断由a、b、c的边长组成的三角形是不是直角三角形:(1) a=15 , b =8 , c=17
(2) a=13 , b =15 , c=14
分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。
五、例题讲解
练习:下面以a,b,c为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) a=25,b=20,c=15 ____ _____ ;
(2) a=13,b=13,c=15 ____ _____ ;
是
不是
∠ A=900
像25,20,15或者15,8,17这样,能够成为直角三角形三条边长的三个正整数,称为勾股数.
1.请你说出常用的勾股数;
2.一组勾股数的正整数倍一定是勾股数吗?为什么
挑战自我
例2:已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积
A
B
C
D
中考链接
例3: “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
A
B
O
E
N
远航
海天
海天
如图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD,求证:∠AEF=90 .
A
F
E
C
B
D
六、拓展思考
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
七、小结
八、作业
《新观察》P27-28
