2012-2013学年第一学期期末考试九年级数学试题
文档属性
| 名称 | 2012-2013学年第一学期期末考试九年级数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 39.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-20 00:00:00 | ||
图片预览


文档简介
2012-2013学年第一学期期末考试
九年级数学试题
(考试时间:90分钟;满分:120分)
题号
一
二
三
总分
21
22
23
24
25
26
得分
注意事项:1.本试卷共6页,用蓝黑钢笔或圆珠笔直接答在试卷上。
2.答卷前将密封线内的项目填写清楚.
3.请同学们认真审题,并把答案填写在Ⅱ卷的答题纸上.
(Ⅰ卷)
一、选择题(每小题3分,共36分)
1.某商品原价200元,连续两次降价a%后售价为148元,下列所列方程正确的是( )
A. B.
C. D.
2.小明家过年吃饺子,妈妈包了50个肉饺子和70个素饺子,小明在年夜饭中,从中任取一个吃,他吃到素水饺的概率是( )
A. B. C. D.
3.等腰三角形的底和腰是方程的两个根,则这个三角形的周长是( )
A. 8 B. 10 C. 8或10 D. 不能确定
4.下列函数中,二次函数是( )
A. B. C. D.
5.下列结论中正确的有( )个.
①等弧所对的圆周角相等,所对的弦相等;②平分弦的直径垂直于弦;③相等的弦所对的圆心角性的;④相等的圆周角所对的弧不一定相等;⑤最长的弦是直径.
A. 1 B. 2 C. 3 D. 4
6.若A,B,C为二次函数的图象上的三点,则的大小关系是( )
A. B. C. D.
7.抛物线的开口方向、对称轴、顶点坐标分别是( )
A. 开口向上; B. 开口向上;
C. 开口向下; D. 开口向下;
8.已知相交两圆的半径分别为4和7,则它们的圆心距可能是( )
A. 2 B. 3 C. 6 D. 11
9.已知反比例函数的图象如右图所示,则二次函数的图象大致是( )
10. 已知二次函数,当取任意实数时,,则的取值范围是( )
A. ≥ B. > C. ≤ D. <
11.一次函数的图象如图所示,当时,
的取值范围是( )
A. B. C. D.
12.直线与坐标轴交于A、B两点,点C在坐标轴上,△ABC为等腰三角形,则满足条件的点C最多有( )个
A. 5 B. 6 C. 7 D. 8
二、填空题(每小题3分,共24分)
13.当 时,关于的方程是一元二次方程.
14.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,若∠BAC=25°,则
∠P= 度.
15.如图,点A在反比例函数的图象上,AB垂直于轴,
若,那么这个反比例函数的解析式为 .
16.如图:正方形ABCD和OEFG中,点A和点F的坐标分别是(3,2)和(-1,-1),则这两个正方形的位似中心是 .
17.因式分解: .
18.二次函数,当x 时,y随x的增大而增大.
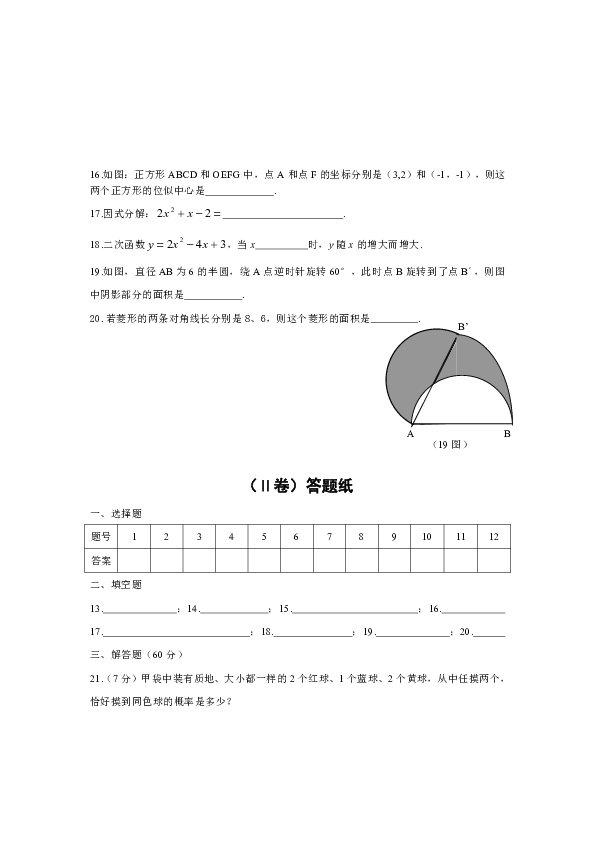
19.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B旋转到了点B′,则图中阴影部分的面积是 .
20.若菱形的两条对角线长分别是8、6,则这个菱形的面积是 .
(Ⅱ卷)答题纸
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题
13. ;14. ;15. ;16.
17. ;18. ;19. ;20.
三、解答题(60分)
21.(7分)甲袋中装有质地、大小都一样的2个红球、1个蓝球、2个黄球,从中任摸两个,恰好摸到同色球的概率是多少?
22.(8分)根据下列条件,分别求出对应的二次函数关系式。
(1)已知抛物线的顶点是(-1,-2),且过点(1,10);
(2)已知抛物线过三点:(0,-2),(1,0),(2,3).
23.(10分)一次函数的图像与反比例函数的图象交于A(-2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△OAB的面积;
(3)写出反比例函数值大于一次函数值的自变量x的取值范围.
24.(10分)如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD⊥AB交半圆于点D,将△ACD沿AD折叠得到△AED,AE交半圆于点F,连接DF.
(1)求证:DE是半圆的切线;
(2)连接OD,当OC=BC时,判断四边形ODFA的形状,并证明你的结论.
25.(12分)如图:在⊙O中,经过⊙O内一点P有一条弦AB,且AP=4,PB=3,过P点另有一条动弦CD(与AB不重合),连接AC,DB.设CP= x,PD=y.
(1)求证:△ACP∽△DBP.
(2)写出y关于 x的函数关系式.
(3)若CD=8时,求的值.
26.(13分)如图,利用一面墙,用80米长的篱笆围成一个矩形场地.
(1)怎样围才能使矩形场地的面积为750平方米?
(2)能否使所围成的矩形面积为810平方米?为什么?
(3)怎样围才能使围成的矩形面积最大?最大是多少?
九年级数学试题
(考试时间:90分钟;满分:120分)
题号
一
二
三
总分
21
22
23
24
25
26
得分
注意事项:1.本试卷共6页,用蓝黑钢笔或圆珠笔直接答在试卷上。
2.答卷前将密封线内的项目填写清楚.
3.请同学们认真审题,并把答案填写在Ⅱ卷的答题纸上.
(Ⅰ卷)
一、选择题(每小题3分,共36分)
1.某商品原价200元,连续两次降价a%后售价为148元,下列所列方程正确的是( )
A. B.
C. D.
2.小明家过年吃饺子,妈妈包了50个肉饺子和70个素饺子,小明在年夜饭中,从中任取一个吃,他吃到素水饺的概率是( )
A. B. C. D.
3.等腰三角形的底和腰是方程的两个根,则这个三角形的周长是( )
A. 8 B. 10 C. 8或10 D. 不能确定
4.下列函数中,二次函数是( )
A. B. C. D.
5.下列结论中正确的有( )个.
①等弧所对的圆周角相等,所对的弦相等;②平分弦的直径垂直于弦;③相等的弦所对的圆心角性的;④相等的圆周角所对的弧不一定相等;⑤最长的弦是直径.
A. 1 B. 2 C. 3 D. 4
6.若A,B,C为二次函数的图象上的三点,则的大小关系是( )
A. B. C. D.
7.抛物线的开口方向、对称轴、顶点坐标分别是( )
A. 开口向上; B. 开口向上;
C. 开口向下; D. 开口向下;
8.已知相交两圆的半径分别为4和7,则它们的圆心距可能是( )
A. 2 B. 3 C. 6 D. 11
9.已知反比例函数的图象如右图所示,则二次函数的图象大致是( )
10. 已知二次函数,当取任意实数时,,则的取值范围是( )
A. ≥ B. > C. ≤ D. <
11.一次函数的图象如图所示,当时,
的取值范围是( )
A. B. C. D.
12.直线与坐标轴交于A、B两点,点C在坐标轴上,△ABC为等腰三角形,则满足条件的点C最多有( )个
A. 5 B. 6 C. 7 D. 8
二、填空题(每小题3分,共24分)
13.当 时,关于的方程是一元二次方程.
14.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,若∠BAC=25°,则
∠P= 度.
15.如图,点A在反比例函数的图象上,AB垂直于轴,
若,那么这个反比例函数的解析式为 .
16.如图:正方形ABCD和OEFG中,点A和点F的坐标分别是(3,2)和(-1,-1),则这两个正方形的位似中心是 .
17.因式分解: .
18.二次函数,当x 时,y随x的增大而增大.
19.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B旋转到了点B′,则图中阴影部分的面积是 .
20.若菱形的两条对角线长分别是8、6,则这个菱形的面积是 .
(Ⅱ卷)答题纸
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题
13. ;14. ;15. ;16.
17. ;18. ;19. ;20.
三、解答题(60分)
21.(7分)甲袋中装有质地、大小都一样的2个红球、1个蓝球、2个黄球,从中任摸两个,恰好摸到同色球的概率是多少?
22.(8分)根据下列条件,分别求出对应的二次函数关系式。
(1)已知抛物线的顶点是(-1,-2),且过点(1,10);
(2)已知抛物线过三点:(0,-2),(1,0),(2,3).
23.(10分)一次函数的图像与反比例函数的图象交于A(-2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△OAB的面积;
(3)写出反比例函数值大于一次函数值的自变量x的取值范围.
24.(10分)如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD⊥AB交半圆于点D,将△ACD沿AD折叠得到△AED,AE交半圆于点F,连接DF.
(1)求证:DE是半圆的切线;
(2)连接OD,当OC=BC时,判断四边形ODFA的形状,并证明你的结论.
25.(12分)如图:在⊙O中,经过⊙O内一点P有一条弦AB,且AP=4,PB=3,过P点另有一条动弦CD(与AB不重合),连接AC,DB.设CP= x,PD=y.
(1)求证:△ACP∽△DBP.
(2)写出y关于 x的函数关系式.
(3)若CD=8时,求的值.
26.(13分)如图,利用一面墙,用80米长的篱笆围成一个矩形场地.
(1)怎样围才能使矩形场地的面积为750平方米?
(2)能否使所围成的矩形面积为810平方米?为什么?
(3)怎样围才能使围成的矩形面积最大?最大是多少?
同课章节目录
