二次函数测试题
图片预览


文档简介
九年级数学二次函数测试题
堡面前中学 班 姓名
一、精心选一选(每小题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.抛物线y=-(x-1)2+3的顶点坐标是
A.(-1,3) B.(1,3) C.(-1,-3) D.(1,-3)
2.抛物线与轴交点的坐标是.
A. B. C. D.
3.已知二次函数有最小值,则与之间的大小关系是.
A. B. C. D.不能确定
4.二次函数的图象与轴交于、两点,与轴相交于点.下列说法中,错误的是.
A.是等腰三角形 B.点的坐标是
C.的长为2 D.随的增大而减小
5.已知二次函数的图象经过原点,则的值为( )
A. 0或2 B. 0 C. 2 D.无法确定
6. 二次函数y=x2的图象向右平移3个单位,得到新的图象的函数表达式是( )
A. y=x2+3 B. y=x2-3 C. y=(x+3)2 D. y=(x-3)2
7.如图,抛物线的函数表达式是.
A. B.
C. D.
8.要得到二次函数的图象,需将的图象.
A.向左平移2个单位,再向下平移2个单位
B.向右平移2个单位,再向上平移2个单位
C.向左平移1个单位,再向上平移1个单位
D.向右平移1个单位,再向下平移1个单位
9.二次函数的图象如图所示,对称
轴是直线,则下列四个结论错误的是.
A. B. C. D.
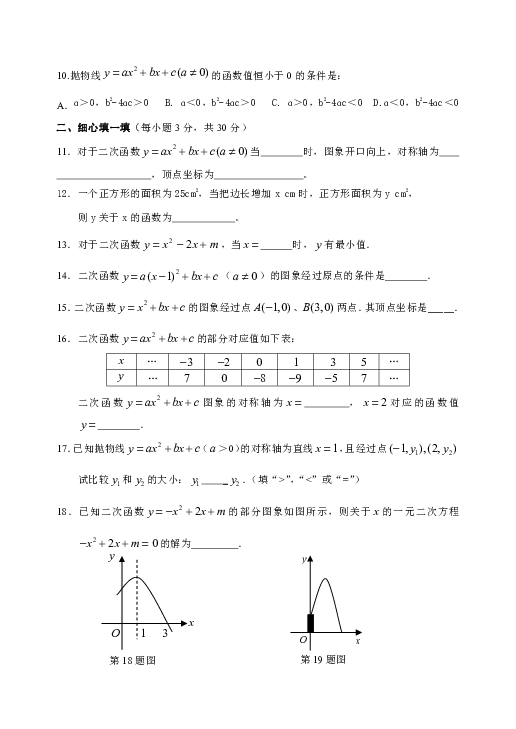
10.抛物线的函数值恒小于0的条件是:
A.ɑ>0,b2-4ɑc>0 B. ɑ<0,b2-4ɑc>0 C. ɑ>0,b2-4ɑc<0 D.ɑ<0,b2-4ɑc<0
二、细心填一填(每小题3分,共30分)
11.对于二次函数当 时,图象开口向上,对称轴为
,顶点坐标为 。
12.一个正方形的面积为25cm2,当把边长增加x cm时,正方形面积为y cm2,
则y关于x的函数为 。
13.对于二次函数,当 时,有最小值.
14.二次函数()的图象经过原点的条件是 .
15.二次函数的图象经过点、两点.其顶点坐标是_____.
16.二次函数的部分对应值如下表:
…
…
…
…
二次函数图象的对称轴为 ,对应的函数值 .
17.已知抛物线(>0)的对称轴为直线,且经过点 试比较和的大小: _.(填“>”,“<”或“=”)
18.已知二次函数的部分图象如图所示,则关于的一元二次方程的解为 .
19.如图所示,阳光中学教学楼前喷水池喷出的抛物线形水柱,其解析式为,则水柱的最大高度是 .
20.如图所示,在同一坐标系中,作出①②③的图象,则图象从里到外的三条抛物线对应的函数依次是(填序号) 。
21世纪教育网三、耐心做一做(共60分)
21.(8分)已知二次函数的顶点坐标为(4,-2),且其图象经过点(5,1),求此二次函数的解析式。
22.(8分)当t取什么值时,抛物线y=2x2-(x+t)2-2与x轴有重合的交点?
23.(12分)用长为20cm的铁丝,折成一个矩形,设它的一边长为xcm,面积为ycm2。
(1)求出y与x的函数关系式。
(2)当边长x为多少时,矩形的面积最大,最大面积是多少?
24.(16分)如图,抛物线与轴交于两点,与轴交于点.
(1)求三点的坐标;
(2)证明为直角三角形;
(3)在抛物线上除点外,是否还存在另外一个点,使是直角三角形,若存在,请求出点的坐标,若不存在,请说明理由.
25.(16分)某商品的进价为每件40元,售价为50元,每个月可以卖出210件;如果每件商品的售价上涨1元,则每个月少卖10件(售价每件不能高于65元)。设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元。
(1)求y与x的函数关系式并直接写出自变量x的取值范围。
(2)每件商品售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰好为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元。
堡面前中学 班 姓名
一、精心选一选(每小题3分,共30分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.抛物线y=-(x-1)2+3的顶点坐标是
A.(-1,3) B.(1,3) C.(-1,-3) D.(1,-3)
2.抛物线与轴交点的坐标是.
A. B. C. D.
3.已知二次函数有最小值,则与之间的大小关系是.
A. B. C. D.不能确定
4.二次函数的图象与轴交于、两点,与轴相交于点.下列说法中,错误的是.
A.是等腰三角形 B.点的坐标是
C.的长为2 D.随的增大而减小
5.已知二次函数的图象经过原点,则的值为( )
A. 0或2 B. 0 C. 2 D.无法确定
6. 二次函数y=x2的图象向右平移3个单位,得到新的图象的函数表达式是( )
A. y=x2+3 B. y=x2-3 C. y=(x+3)2 D. y=(x-3)2
7.如图,抛物线的函数表达式是.
A. B.
C. D.
8.要得到二次函数的图象,需将的图象.
A.向左平移2个单位,再向下平移2个单位
B.向右平移2个单位,再向上平移2个单位
C.向左平移1个单位,再向上平移1个单位
D.向右平移1个单位,再向下平移1个单位
9.二次函数的图象如图所示,对称
轴是直线,则下列四个结论错误的是.
A. B. C. D.
10.抛物线的函数值恒小于0的条件是:
A.ɑ>0,b2-4ɑc>0 B. ɑ<0,b2-4ɑc>0 C. ɑ>0,b2-4ɑc<0 D.ɑ<0,b2-4ɑc<0
二、细心填一填(每小题3分,共30分)
11.对于二次函数当 时,图象开口向上,对称轴为
,顶点坐标为 。
12.一个正方形的面积为25cm2,当把边长增加x cm时,正方形面积为y cm2,
则y关于x的函数为 。
13.对于二次函数,当 时,有最小值.
14.二次函数()的图象经过原点的条件是 .
15.二次函数的图象经过点、两点.其顶点坐标是_____.
16.二次函数的部分对应值如下表:
…
…
…
…
二次函数图象的对称轴为 ,对应的函数值 .
17.已知抛物线(>0)的对称轴为直线,且经过点 试比较和的大小: _.(填“>”,“<”或“=”)
18.已知二次函数的部分图象如图所示,则关于的一元二次方程的解为 .
19.如图所示,阳光中学教学楼前喷水池喷出的抛物线形水柱,其解析式为,则水柱的最大高度是 .
20.如图所示,在同一坐标系中,作出①②③的图象,则图象从里到外的三条抛物线对应的函数依次是(填序号) 。
21世纪教育网三、耐心做一做(共60分)
21.(8分)已知二次函数的顶点坐标为(4,-2),且其图象经过点(5,1),求此二次函数的解析式。
22.(8分)当t取什么值时,抛物线y=2x2-(x+t)2-2与x轴有重合的交点?
23.(12分)用长为20cm的铁丝,折成一个矩形,设它的一边长为xcm,面积为ycm2。
(1)求出y与x的函数关系式。
(2)当边长x为多少时,矩形的面积最大,最大面积是多少?
24.(16分)如图,抛物线与轴交于两点,与轴交于点.
(1)求三点的坐标;
(2)证明为直角三角形;
(3)在抛物线上除点外,是否还存在另外一个点,使是直角三角形,若存在,请求出点的坐标,若不存在,请说明理由.
25.(16分)某商品的进价为每件40元,售价为50元,每个月可以卖出210件;如果每件商品的售价上涨1元,则每个月少卖10件(售价每件不能高于65元)。设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元。
(1)求y与x的函数关系式并直接写出自变量x的取值范围。
(2)每件商品售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰好为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元。
