北师大版八年级数学下册 3.2图形的旋转 教学设计(表格式)
文档属性
| 名称 | 北师大版八年级数学下册 3.2图形的旋转 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 228.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 00:00:00 | ||
图片预览


文档简介
一、基本信息
学校
课名 《图形的旋转》 教师姓名
学科(版本) 北师大版数学 章节 第三章第二节第一课时
学时 1 年级 八年级下
二、教学目标 1.掌握旋转的定义,会确定旋转前后图形的对应点、对应线段、对应角、旋转中心、旋转角; 2.理解图形的旋转是由旋转中心、旋转角和旋转方向所决定的,探索和发现任意一组对应点与旋转中心连续所夹的角都是旋转角; 3.通过观察、操作、交流、归纳培养学生的动手能力、观察能力、探究问题的能力以及与人合作交流的能力。
三、学习者分析 学生的知识技能基础:学生在初一下全等三角形的学习中,已经见过了很多以旋转变换为基础的全等三角形,对旋转变换的图形有熟悉感,同时学生也具备了一定的逻辑推理能力,为本节课做了一定的知识储备,但由于初二学生在几何直观上还有所欠缺,对于图形的运动仍然比较陌生,本课知识对他们而言难度较大; 学生的活动经验基础:本课是一堂以学生活动为主的新授课,而几何画板是本课的一个重要组成部分,在之前的教学中,已经涉及过几何画板的操作,学生也已具备了几何画板的操作和分析的能力,会通过观察读取其中的信息,并猜想和归纳。
四、教学重难点分析及解决措施 教学重点:旋转的定义和性质 教学难点:定义的形成和性质的探究过程 教学策略:通过班内几位小演员表演的一个简短小品,让学生感受旋转的三个要素,再通过将生活场景抽象为平面图形,以填空的形式指导学生准确地描述旋转,在充分感受后,自然地引出旋转的定义。而在定义后通过动态图的反复呈现,刺激学生的视觉,并由学生找出这几个图形中的旋转三要素和对应角及对应边,一方面加深学生对旋转的理解,另一方面为性质的探索打下基础。接着以锦囊的形式设置悬念,激发学生的兴趣,并将三个锦囊赠予学生,其实锦囊就是三个几何画板程序,推送给他们之后,他们自己在平板上操作,通过特制表格的填写来梳理旋转的性质,并通过用符号语言对性质的描述加深学生对性质的理解。
五、教学设计
教学环节 起止时间(’”- ’”) 环节目标 教学内容 学生活动 媒体作用及分析
我比你猜——游戏引入 0’0”-1’46” 通过情景竞猜,学生回忆生活中的旋转,引入新课 三位同学表演四个生活中的旋转场景:芭蕾,风车,挂钟,秋千,由其他同学来猜,体会生活中常见的旋转现象。 表演的同学表演,其他同学猜 利用PPT呈现动态图片,再现生活情景。
我说你做 ——初识旋转三要素 3’45”-3’28” 通过情景表演,由学生来提出旋转的三个要素:中心,方向,角度 五位同学小品表演,一人说口令“转”,其余四人以不同的中心,不同的方向,不同的角度旋转,制造笑料,在同学们的笑声之后,教师设问:“是口令的问题还是四位听口令的同学的问题?问题又出在哪?”其他同学回答,并答出了口令的问题——没有指出转动的方向,角度和中心。 表演的同学表演小品,问题百出,笑料不断,其他同学分析原因,感受旋转的三要素。 PPT动画呈现“中心、角度、方向”
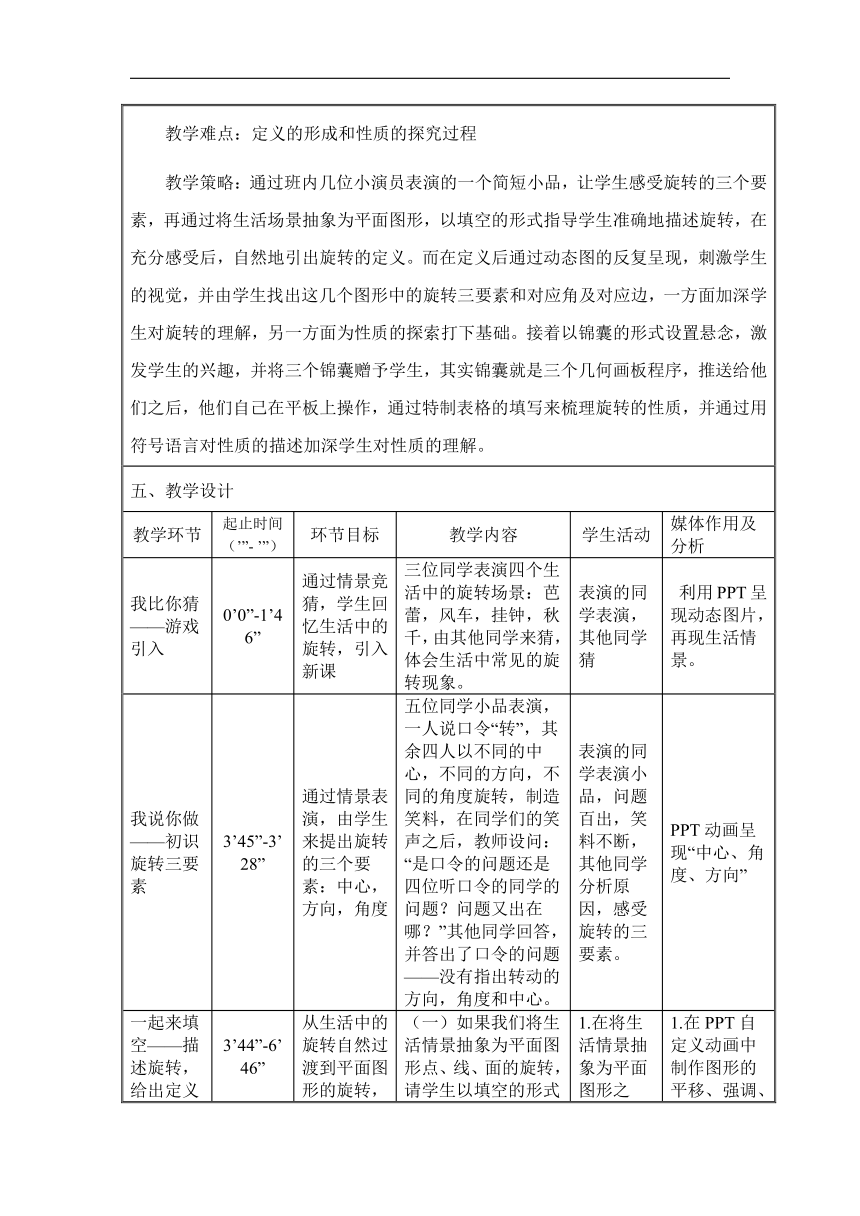
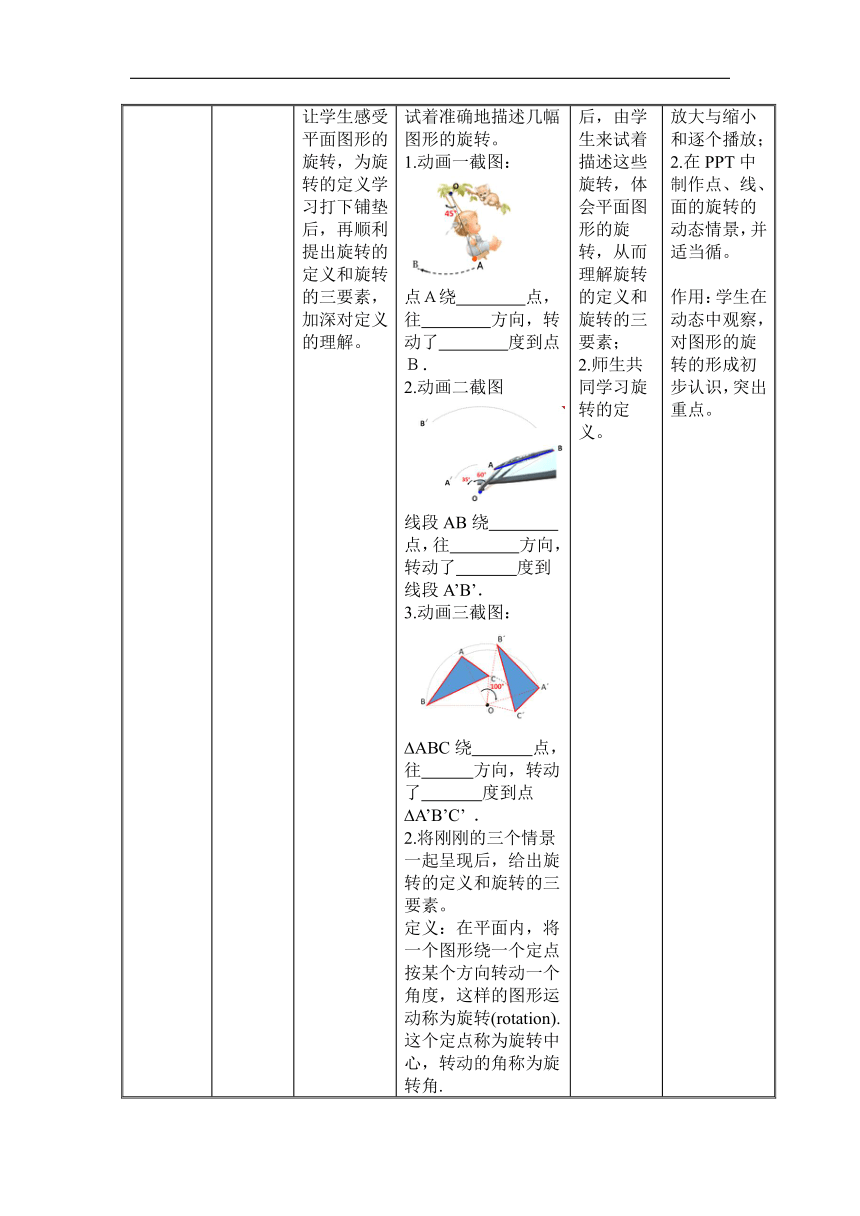
一起来填空——描述旋转,给出定义 3’44”-6’46” 从生活中的旋转自然过渡到平面图形的旋转,让学生感受平面图形的旋转,为旋转的定义学习打下铺垫后,再顺利提出旋转的定义和旋转的三要素,加深对定义的理解。 (一)如果我们将生活情景抽象为平面图形点、线、面的旋转,请学生以填空的形式试着准确地描述几幅图形的旋转。 1.动画一截图: 点A绕 点,往 方向,转动了 度到点B. 2.动画二截图 线段AB绕 点,往 方向,转动了 度到线段A’B’. 3.动画三截图: ABC绕 点,往 方向,转动了 度到点 A’B’C’ . 2.将刚刚的三个情景一起呈现后,给出旋转的定义和旋转的三要素。 定义:在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转(rotation). 这个定点称为旋转中心,转动的角称为旋转角. 旋转的三要素: 旋转中心,旋转方向, 旋转角度. 1.在将生活情景抽象为平面图形之后,由学生来试着描述这些旋转,体会平面图形的旋转,从而理解旋转的定义和旋转的三要素; 2.师生共同学习旋转的定义。 1.在PPT自定义动画中制作图形的平移、强调、放大与缩小和逐个播放; 2.在PPT中制作点、线、面的旋转的动态情景,并适当循。 作用:学生在动态中观察,对图形的旋转的形成初步认识,突出重点。
看谁反应快——熟悉定义和旋转三要素 6’47”-11’00” 以直观的运动的旋转图片反复刺激学生的视觉神经,加深学生对旋转的认识,并通过找旋转三要素,为旋转性质的探索做好知识储备。 展示三个动态旋转图片,图片会循环播放,学生观察图形并回答对应的问题。 (一)动图一截图: 问题: 1.说出旋转中心 2.说出旋转方向 3.找出旋转角 4.说出对应点 (二)动图二截图: 1.说出旋转中心 2.说出旋转方向 3.找出旋转角 4.说出对应线段 5.找出对应角 (三)动图三截图: 1.说出旋转中心 2.说出旋转方向 3.说出旋转角 4. 说出对应点和对应线段 教学效果:这些问题学生基本能回答正确,同时部分问题仍需要教师的指导。 学生思考并回答提出的问题,熟悉旋转的定义和三要素 1.用几何画板制作图形的旋转动画,再利用录屏软件录下旋转过程生成为gif格式动态图片并以复制粘贴的方式插入PPT,循环,反复播放。 2.在几何画板中截取一副静图。和动图一起插入PPT中。 作用:旋转本身就是图形的变换,是动态的,在学生的学习之初,理应是动态的理解。旋转角的确定是旋转的一大难点,通过新技术的引入,反复的形象的视觉冲击让学生在直观的图形中,更容易找出旋转角。
锦囊答惑——旋转性质探索 12’20”-26’58” 1.学生通过自己对几何画板的操作和观察,获得对旋转性质的初步感受。 2.通过表格的填写,对已有的知识体验进行梳理。 3.小组成员共同谈论表格中的的特点,试着归纳旋转的性质,实现自己对知识的获取。 4.教师只需对学生的总结进行语言的规范化指导,让学生从本质上理解旋转的性质。 (一)教师展示学生在《全等三角形》一章的学习中遇到的一些的由旋转变换形成的全等三角形,唤醒知识,并设问, 1.对应点和旋转中心有何关系? 2.对应线段有何关系? 3.对应角有什么关系? 4.旋转角和图形的对应点之间有什么关系? 教学效果:部分问题学生能回答,部分理解题目就有困难,这个不重要,以这些问题开启对旋转的性质的探索。 (二)在学生疑惑时,赠予学生三个锦囊,每个锦囊都链接一个几何画板的程序,把这些程序推送至学生平板,他们在自己的平板上按键,观察,发现,三个几何画板程序,分别是点的旋转,线的旋转和三角形的旋转,在每个程序里面都设计了几个按键,学生可以按动“动画”键让图形运动起来或停下来;也可以按动“显示线段OA和OA'”键来观察对应点与旋转中心连线的数量关系,还可以在动态变化或静止状态下观察∠BOB'和∠AOA'的大小关系,学生对性质也就有了更直观的感受; 1.锦囊一截图: 2.锦囊二截图: 3.锦囊三截图: 教学效果:锦囊激发了学生的好奇心,他们非常想知道锦囊里装的什么,引起了课堂的一个小高潮,而通过近距离地操作旋转,对旋转的性质有一些感受,但还不足以归纳出性质。 (三)学生打开一个锦囊并完成该图形所对应的任务。任务见下表: 教学效果:通过表格填写,大部分学生心中都有了一些相等线段和相等角,但归纳出完整的性质仍有困难。 (四)小组讨论思考,从表格的每一列你能得出哪些结论呢? 小组讨论后发表小组见解。 教学效果:对性质中的对应线段相等,对应角相等学生能自主归纳,也能从第二列中归纳出对应点与旋转中心距离相等,但对于第四列学生会归纳为“旋转角相等”教师指导并归纳为:任意一组对应点和旋转中心连线所成的夹角都是旋转角; (五)师生一起归纳旋转的性质,规范学生的语言; 教学效果:有了之前大量的活动经验,学生基本能理解记忆旋转的性质。 (六)让学生观察下图,并试着将旋转的性质,用符号语言来描述,进一步熟悉旋转的性质。 教学效果:有了符号语言的描述,学生对∠AOA'=∠BOB'=∠COC'也有了更深的理解。 1.学生操作几何画板软件,独立填写表格; 2.学生分享自己的表格; 3.小组合作讨论旋转的性质特征; 4.师生一起归纳旋转的性质; 5.通过对性质进行符号语言的描述,师生一起再次熟悉旋转的性质。 1.用几何画板制作了点的旋转,三角形的旋转和线段的旋转;2.在程序中设计了“动画”键控制图形的静止和运动,“显示和隐藏OA和OA'”键控制两条线段的显示和隐藏。 3.程序中显示 OA和OA'的在旋转过程中的长度值; 4.显示∠BOB'和∠AOA'在旋转过程中的度数值。 5.在PPT中插入超链接,链接至几何画板程序。 作用:学生自己操作软件,他们亲身感受旋转的动态和静态,并且几何画板软件几个按键的设置让学生在动与静之间观察图形,在直观的图形中也更容易探索旋转的性质。
小试牛刀——旋转性质初步应用 27’07”-33’24” 通过练习,让学生熟悉旋转的性质,并尝试用旋转的性质来解决问题。 向学生推送三道即时练习,指向旋转性质的三个维度——对应边,对应角,旋转角的关系。 1.如图,小林坐在秋千上,秋千旋转了80°,小林的位置也从A点运动到了A'点,则∠OAA'的度数为( ) A.40° B.50° C.70° D.80° 2.如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( ) A.115° B.120° C.125° D.145° 3.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则线段BD的长为( ) A.2 B.2 C.4 D.2 教学效果:三个问题,大多数学生能独立解决并正确解答。 1.学生思考问题并在平板上回答; 2.由学生自己来讲解解题思路。 利用未来课堂程序,截取屏幕向学生推送3个选择题,学生在平板答题后,在未来课堂系统里进行统计答题效果。 作用:教师能第一时间知道学生对知识的掌握情况,动态地把握课堂。
知识重现——典例讲解 33’25”-40’24” 学生通过例题进一步熟悉旋转的性质,学会用旋转的性质解决问题。 (一)教师呈现一道在之前学习中所遇到过的一个问题,推送给学生,先由学生自主思考解题方法,试着用旋转的性质解决问题,例题入下: 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,将△APB绕点B逆时针旋转一定角度后,可得到△CQB. (1)求点P与点Q之间的距离; (2)求∠APB的度数. (二)学生在平板答题或在学案上答题,并及时将自己的答题上传; (三)在上传的解答中,展示某位同学的解答过程,师生共同探讨有了旋转的性质,解法上是否有所不同。学生对于对应边角相等会很好地应用,教师即时点拨在确∠PBQ=60°时可以直接用性质三,任意一组对应点和旋转中心连线所成的夹角都是旋转角∠PBQ=∠ABC=60°。从而升华本课知识。 学生自主答题,并通过同学的展示思考问题的最优解决方案。 1.利用未来课堂程序,截取屏幕向学生推送解答题,学生在平板答题或在学案答题,如果在学案答题则通过对答题过程进行拍照上传提交解题过程。 2.在未来课堂系统里观察提交情况和答题情况。 作用:在未来课堂的软件中,学生能知道自己的答题时间,教师能知道学生的答题速度,可以看学生个人的答题,及时捕捉学生的疑惑点,从而及时调整课堂的进度和难度。
知识小结 40’25”-41’26” 在师生的共同回忆中,提炼出本课的要点,让学生清楚地知道本课的教学重难点。 师生共同小结本课知识: 1.旋转定义 2.旋转的基本性质: ◆对应点到旋转中心的距离相等; ◆对应线段相等,对应角相等 ◆任意一组对应点与旋转中心的连线所成的角都等于旋转角 学生回忆在课堂中的几个主要知识点 PPT展示教学主要知识点
学校
课名 《图形的旋转》 教师姓名
学科(版本) 北师大版数学 章节 第三章第二节第一课时
学时 1 年级 八年级下
二、教学目标 1.掌握旋转的定义,会确定旋转前后图形的对应点、对应线段、对应角、旋转中心、旋转角; 2.理解图形的旋转是由旋转中心、旋转角和旋转方向所决定的,探索和发现任意一组对应点与旋转中心连续所夹的角都是旋转角; 3.通过观察、操作、交流、归纳培养学生的动手能力、观察能力、探究问题的能力以及与人合作交流的能力。
三、学习者分析 学生的知识技能基础:学生在初一下全等三角形的学习中,已经见过了很多以旋转变换为基础的全等三角形,对旋转变换的图形有熟悉感,同时学生也具备了一定的逻辑推理能力,为本节课做了一定的知识储备,但由于初二学生在几何直观上还有所欠缺,对于图形的运动仍然比较陌生,本课知识对他们而言难度较大; 学生的活动经验基础:本课是一堂以学生活动为主的新授课,而几何画板是本课的一个重要组成部分,在之前的教学中,已经涉及过几何画板的操作,学生也已具备了几何画板的操作和分析的能力,会通过观察读取其中的信息,并猜想和归纳。
四、教学重难点分析及解决措施 教学重点:旋转的定义和性质 教学难点:定义的形成和性质的探究过程 教学策略:通过班内几位小演员表演的一个简短小品,让学生感受旋转的三个要素,再通过将生活场景抽象为平面图形,以填空的形式指导学生准确地描述旋转,在充分感受后,自然地引出旋转的定义。而在定义后通过动态图的反复呈现,刺激学生的视觉,并由学生找出这几个图形中的旋转三要素和对应角及对应边,一方面加深学生对旋转的理解,另一方面为性质的探索打下基础。接着以锦囊的形式设置悬念,激发学生的兴趣,并将三个锦囊赠予学生,其实锦囊就是三个几何画板程序,推送给他们之后,他们自己在平板上操作,通过特制表格的填写来梳理旋转的性质,并通过用符号语言对性质的描述加深学生对性质的理解。
五、教学设计
教学环节 起止时间(’”- ’”) 环节目标 教学内容 学生活动 媒体作用及分析
我比你猜——游戏引入 0’0”-1’46” 通过情景竞猜,学生回忆生活中的旋转,引入新课 三位同学表演四个生活中的旋转场景:芭蕾,风车,挂钟,秋千,由其他同学来猜,体会生活中常见的旋转现象。 表演的同学表演,其他同学猜 利用PPT呈现动态图片,再现生活情景。
我说你做 ——初识旋转三要素 3’45”-3’28” 通过情景表演,由学生来提出旋转的三个要素:中心,方向,角度 五位同学小品表演,一人说口令“转”,其余四人以不同的中心,不同的方向,不同的角度旋转,制造笑料,在同学们的笑声之后,教师设问:“是口令的问题还是四位听口令的同学的问题?问题又出在哪?”其他同学回答,并答出了口令的问题——没有指出转动的方向,角度和中心。 表演的同学表演小品,问题百出,笑料不断,其他同学分析原因,感受旋转的三要素。 PPT动画呈现“中心、角度、方向”
一起来填空——描述旋转,给出定义 3’44”-6’46” 从生活中的旋转自然过渡到平面图形的旋转,让学生感受平面图形的旋转,为旋转的定义学习打下铺垫后,再顺利提出旋转的定义和旋转的三要素,加深对定义的理解。 (一)如果我们将生活情景抽象为平面图形点、线、面的旋转,请学生以填空的形式试着准确地描述几幅图形的旋转。 1.动画一截图: 点A绕 点,往 方向,转动了 度到点B. 2.动画二截图 线段AB绕 点,往 方向,转动了 度到线段A’B’. 3.动画三截图: ABC绕 点,往 方向,转动了 度到点 A’B’C’ . 2.将刚刚的三个情景一起呈现后,给出旋转的定义和旋转的三要素。 定义:在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转(rotation). 这个定点称为旋转中心,转动的角称为旋转角. 旋转的三要素: 旋转中心,旋转方向, 旋转角度. 1.在将生活情景抽象为平面图形之后,由学生来试着描述这些旋转,体会平面图形的旋转,从而理解旋转的定义和旋转的三要素; 2.师生共同学习旋转的定义。 1.在PPT自定义动画中制作图形的平移、强调、放大与缩小和逐个播放; 2.在PPT中制作点、线、面的旋转的动态情景,并适当循。 作用:学生在动态中观察,对图形的旋转的形成初步认识,突出重点。
看谁反应快——熟悉定义和旋转三要素 6’47”-11’00” 以直观的运动的旋转图片反复刺激学生的视觉神经,加深学生对旋转的认识,并通过找旋转三要素,为旋转性质的探索做好知识储备。 展示三个动态旋转图片,图片会循环播放,学生观察图形并回答对应的问题。 (一)动图一截图: 问题: 1.说出旋转中心 2.说出旋转方向 3.找出旋转角 4.说出对应点 (二)动图二截图: 1.说出旋转中心 2.说出旋转方向 3.找出旋转角 4.说出对应线段 5.找出对应角 (三)动图三截图: 1.说出旋转中心 2.说出旋转方向 3.说出旋转角 4. 说出对应点和对应线段 教学效果:这些问题学生基本能回答正确,同时部分问题仍需要教师的指导。 学生思考并回答提出的问题,熟悉旋转的定义和三要素 1.用几何画板制作图形的旋转动画,再利用录屏软件录下旋转过程生成为gif格式动态图片并以复制粘贴的方式插入PPT,循环,反复播放。 2.在几何画板中截取一副静图。和动图一起插入PPT中。 作用:旋转本身就是图形的变换,是动态的,在学生的学习之初,理应是动态的理解。旋转角的确定是旋转的一大难点,通过新技术的引入,反复的形象的视觉冲击让学生在直观的图形中,更容易找出旋转角。
锦囊答惑——旋转性质探索 12’20”-26’58” 1.学生通过自己对几何画板的操作和观察,获得对旋转性质的初步感受。 2.通过表格的填写,对已有的知识体验进行梳理。 3.小组成员共同谈论表格中的的特点,试着归纳旋转的性质,实现自己对知识的获取。 4.教师只需对学生的总结进行语言的规范化指导,让学生从本质上理解旋转的性质。 (一)教师展示学生在《全等三角形》一章的学习中遇到的一些的由旋转变换形成的全等三角形,唤醒知识,并设问, 1.对应点和旋转中心有何关系? 2.对应线段有何关系? 3.对应角有什么关系? 4.旋转角和图形的对应点之间有什么关系? 教学效果:部分问题学生能回答,部分理解题目就有困难,这个不重要,以这些问题开启对旋转的性质的探索。 (二)在学生疑惑时,赠予学生三个锦囊,每个锦囊都链接一个几何画板的程序,把这些程序推送至学生平板,他们在自己的平板上按键,观察,发现,三个几何画板程序,分别是点的旋转,线的旋转和三角形的旋转,在每个程序里面都设计了几个按键,学生可以按动“动画”键让图形运动起来或停下来;也可以按动“显示线段OA和OA'”键来观察对应点与旋转中心连线的数量关系,还可以在动态变化或静止状态下观察∠BOB'和∠AOA'的大小关系,学生对性质也就有了更直观的感受; 1.锦囊一截图: 2.锦囊二截图: 3.锦囊三截图: 教学效果:锦囊激发了学生的好奇心,他们非常想知道锦囊里装的什么,引起了课堂的一个小高潮,而通过近距离地操作旋转,对旋转的性质有一些感受,但还不足以归纳出性质。 (三)学生打开一个锦囊并完成该图形所对应的任务。任务见下表: 教学效果:通过表格填写,大部分学生心中都有了一些相等线段和相等角,但归纳出完整的性质仍有困难。 (四)小组讨论思考,从表格的每一列你能得出哪些结论呢? 小组讨论后发表小组见解。 教学效果:对性质中的对应线段相等,对应角相等学生能自主归纳,也能从第二列中归纳出对应点与旋转中心距离相等,但对于第四列学生会归纳为“旋转角相等”教师指导并归纳为:任意一组对应点和旋转中心连线所成的夹角都是旋转角; (五)师生一起归纳旋转的性质,规范学生的语言; 教学效果:有了之前大量的活动经验,学生基本能理解记忆旋转的性质。 (六)让学生观察下图,并试着将旋转的性质,用符号语言来描述,进一步熟悉旋转的性质。 教学效果:有了符号语言的描述,学生对∠AOA'=∠BOB'=∠COC'也有了更深的理解。 1.学生操作几何画板软件,独立填写表格; 2.学生分享自己的表格; 3.小组合作讨论旋转的性质特征; 4.师生一起归纳旋转的性质; 5.通过对性质进行符号语言的描述,师生一起再次熟悉旋转的性质。 1.用几何画板制作了点的旋转,三角形的旋转和线段的旋转;2.在程序中设计了“动画”键控制图形的静止和运动,“显示和隐藏OA和OA'”键控制两条线段的显示和隐藏。 3.程序中显示 OA和OA'的在旋转过程中的长度值; 4.显示∠BOB'和∠AOA'在旋转过程中的度数值。 5.在PPT中插入超链接,链接至几何画板程序。 作用:学生自己操作软件,他们亲身感受旋转的动态和静态,并且几何画板软件几个按键的设置让学生在动与静之间观察图形,在直观的图形中也更容易探索旋转的性质。
小试牛刀——旋转性质初步应用 27’07”-33’24” 通过练习,让学生熟悉旋转的性质,并尝试用旋转的性质来解决问题。 向学生推送三道即时练习,指向旋转性质的三个维度——对应边,对应角,旋转角的关系。 1.如图,小林坐在秋千上,秋千旋转了80°,小林的位置也从A点运动到了A'点,则∠OAA'的度数为( ) A.40° B.50° C.70° D.80° 2.如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( ) A.115° B.120° C.125° D.145° 3.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则线段BD的长为( ) A.2 B.2 C.4 D.2 教学效果:三个问题,大多数学生能独立解决并正确解答。 1.学生思考问题并在平板上回答; 2.由学生自己来讲解解题思路。 利用未来课堂程序,截取屏幕向学生推送3个选择题,学生在平板答题后,在未来课堂系统里进行统计答题效果。 作用:教师能第一时间知道学生对知识的掌握情况,动态地把握课堂。
知识重现——典例讲解 33’25”-40’24” 学生通过例题进一步熟悉旋转的性质,学会用旋转的性质解决问题。 (一)教师呈现一道在之前学习中所遇到过的一个问题,推送给学生,先由学生自主思考解题方法,试着用旋转的性质解决问题,例题入下: 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,将△APB绕点B逆时针旋转一定角度后,可得到△CQB. (1)求点P与点Q之间的距离; (2)求∠APB的度数. (二)学生在平板答题或在学案上答题,并及时将自己的答题上传; (三)在上传的解答中,展示某位同学的解答过程,师生共同探讨有了旋转的性质,解法上是否有所不同。学生对于对应边角相等会很好地应用,教师即时点拨在确∠PBQ=60°时可以直接用性质三,任意一组对应点和旋转中心连线所成的夹角都是旋转角∠PBQ=∠ABC=60°。从而升华本课知识。 学生自主答题,并通过同学的展示思考问题的最优解决方案。 1.利用未来课堂程序,截取屏幕向学生推送解答题,学生在平板答题或在学案答题,如果在学案答题则通过对答题过程进行拍照上传提交解题过程。 2.在未来课堂系统里观察提交情况和答题情况。 作用:在未来课堂的软件中,学生能知道自己的答题时间,教师能知道学生的答题速度,可以看学生个人的答题,及时捕捉学生的疑惑点,从而及时调整课堂的进度和难度。
知识小结 40’25”-41’26” 在师生的共同回忆中,提炼出本课的要点,让学生清楚地知道本课的教学重难点。 师生共同小结本课知识: 1.旋转定义 2.旋转的基本性质: ◆对应点到旋转中心的距离相等; ◆对应线段相等,对应角相等 ◆任意一组对应点与旋转中心的连线所成的角都等于旋转角 学生回忆在课堂中的几个主要知识点 PPT展示教学主要知识点
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
