2.2.1用样本的频率分布估计总体分布(下)
文档属性
| 名称 | 2.2.1用样本的频率分布估计总体分布(下) |
|
|
| 格式 | zip | ||
| 文件大小 | 777.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-20 00:00:00 | ||
图片预览



文档简介
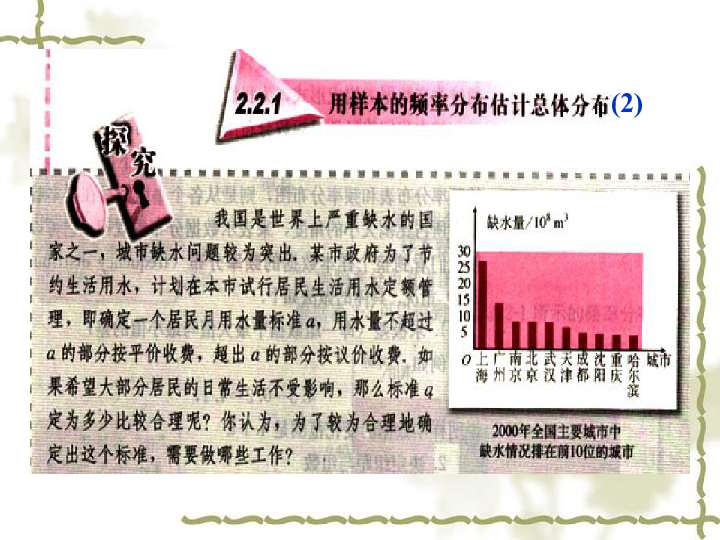
课件27张PPT。(2)1、求极差(即一组数据中最大值与最小值的差)
知道这组数据的变动范围4.3-0.2=4.12、决定组距与组数(将数据分组)3、 将数据分组(8.2取整,分为9组)复习:画频率分布直方图的步骤4、列出频率分布表.5、画出频率分布直方图。组距:指每个小组的两个端点的距离
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组。
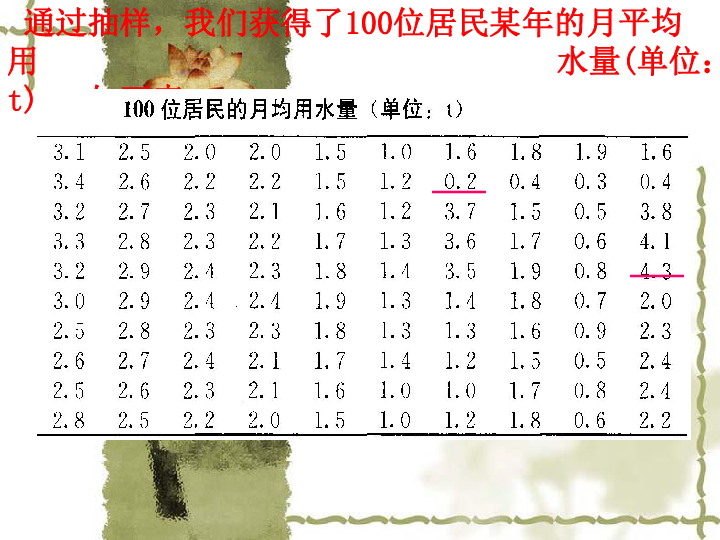
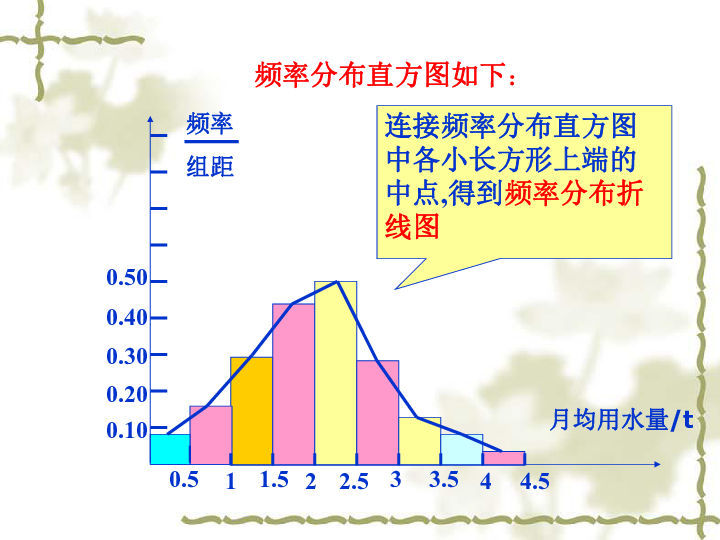
通过抽样,我们获得了100位居民某年的月平均用 水量(单位:t) ,如下表: 频率分布直方图如下:连接频率分布直方图中各小长方形上端的中点,得到频率分布折线图利用样本频分布对总体分布进行相应估计(3)当样本容量无限增大,组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线——总体密度曲线。(2)样本容量越大,这种估计越精确。(1)上例的样本容量为100,如果增至1000,其频率分布直方图的情况会有什么变化?假如增至10000呢?总体密度曲线月均用水量/tab (图中阴影部分的面积,表示总体在某个区间 (a, b) 内取值的百分比)。引入:某篮球运动员在某赛季各场比赛的得分情况如下:
12,15,24,25,31,31,36,37,39,44,49,50.问题1:如何分析该运动员的整体水平及发挥的稳定程度?问题2:初中统计部分曾学过用什么来反映总体的水平?用什么来考察稳定程度? 用样本分布直方图去估计相应的总体分布时,一般样本容量越大,频率分布直方图就会无限接近总体密度曲线,就越精确地反映了总体的分布规律,即越精确地反映了总体在各个范围内取值百分比。 总体密度曲线反映了总体在各个范围内取值的百分比,精确地反映了总体的分布规律。是研究总体分布的工具.总体密度曲线 在初中我们学过用平均数、众数和中位数反映总体的水平,用方差考察稳定程度。 我们还有一种简易的方法,就是将这些数据有条理的列出来,从中观察数据的分布情况,这种方法就是我们今天要学习的茎叶图。制作茎叶图的方法是:将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出.茎叶图的制作方法注意:在制作茎叶图时,重复出现的数据要重复记录,不能遗漏,特别是“叶”部分;同一数据出现几次,就要在图中体现几次.茎叶图某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:(1)甲运动员得分:
13,51,23,8,26,38,16,33,14,28,39(1)乙运动员得分: 49,24,12,31,50,31,44,36,15,37,25,36,39茎叶图甲乙0
1
2
3
4
5
2 5
5 4
1 6 1 6 7 9
4 9
08
4 6 3
6 8
3 8 9
1 叶就是从茎的旁边生长出来的数,表示得分的个位数。 茎是指中间的一列数,表示得分的十位数茎叶图的特征
1.用茎叶图表示数据有两个优点:一是从统计图
上没有原始数据信息的损失,所有数据信息都可
以从茎叶图中得到;二是茎叶图中的数据可以随
时记录,随时添加,方便记录与表示。
2.茎叶图只便于表示两位有效数字的数据,而且
茎叶图只方便记录两组的数据,两个以上的数据
虽然能够记录,但是没有表示两个记录那么直观、
清晰。分析:茎是指中间的一列数,叶就是从茎的旁
边生长出来的数。中间的数字表示得分的十位
数,旁边的数字分别表示两个人得分的个位数。
乙运动员的得分基本上是对称的,叶的分布是
“单峰”的,有的叶集中在茎2,3,4上,中位数
是36;甲运动员的得分除一个特殊得分(51分)
外,也大致对称,叶的分布也是“单峰”的,的叶
集中在茎1,2,3上,中位数是26。由此可看出,
乙运动员的成绩更好。另外,从叶在茎上的分布
情况看,乙运动员的得分集中于峰值附近,这说
明乙运动员的发挥更稳定.例3. 某中学高一(2) 班甲、乙两名同学自高中
以来每场数学考试成绩情况如下:
甲的得分:95,81,75,91,86,89,71,65,76,
88,94,110,107;
乙的得分:83,86,93,99,88,103,98,114,
98,79,101.
画出两人数学成绩的茎叶图,请根据茎叶图对
两人的成绩进行比较.分析:用中间的数字表示两位同学得分的十位数和
百位数.两边的数字分别表示两人每场数学考试成
绩的个位数.解:甲、乙两人数学成绩的茎叶图如下图. 从这个茎叶图上可以看出 乙同学的得分情况是大
致对称的,中位数是98;甲同学的得分情况除一个特殊
得分(110分)外. 也大致对称,中位数是88.因此乙
同学发挥比较稳定,总体得分情况比甲同学好. 例题4:有一个容量为50的样本,其数
据的茎叶图表示如下:
茎 叶
1 34566678888999
2 0000112222233334455566667778889
3 01123
将其分成7组并要求:
(1)列出样本的频率分布表;
(2)画出频率分布直方图以及频率分布折线图. 1.一次选拔运动员,测得7名选手的身高(单位:cm)分布茎叶图如图,记录的平均身高为177 cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为( )
A.5 B.6
C.7 D.8
解析:选D.由题意可知,3+4-7-4+(x-7)+1+2=0,解得x=8.随堂练习2.甲、乙两位同学某学科的连续五次考试成绩用茎叶图表示如右:则平均分数较高的是__________,成绩较为稳定的是__________.
答案:甲 甲随堂练习巩固练习:
1、甲、乙两篮球运动员上赛季每场比赛的得分如下,
甲 12,15,24,25,31,31,36,36,37,39,44,49,50
乙 8,13,14,16,23,26,28,33,
38,39,51
试用茎叶图将这些数据列出来,观察数据的分布情况,比较这两位运动员的得分水平.
2.下面是甲、乙两名运动员某赛季一些场次得分的茎叶图:(1)甲,乙两名队员的
最高得分各是多少?(2)哪名运动员
的成绩好一些?3.有一个容量为50的样本,其数据的茎叶图表示如下:
?
?
?
?
?
将其分成7组并要求:
(1)列出样本的频率分布表;
(2)画出频率分布直方图以及密度曲线 1
2
3
34566678888999
0000112222233334455566667778889
01123
作业:
P71练习:3.
P81习题2.2 A组:
1.(1)(2)(3).
知道这组数据的变动范围4.3-0.2=4.12、决定组距与组数(将数据分组)3、 将数据分组(8.2取整,分为9组)复习:画频率分布直方图的步骤4、列出频率分布表.5、画出频率分布直方图。组距:指每个小组的两个端点的距离
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组。
通过抽样,我们获得了100位居民某年的月平均用 水量(单位:t) ,如下表: 频率分布直方图如下:连接频率分布直方图中各小长方形上端的中点,得到频率分布折线图利用样本频分布对总体分布进行相应估计(3)当样本容量无限增大,组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线——总体密度曲线。(2)样本容量越大,这种估计越精确。(1)上例的样本容量为100,如果增至1000,其频率分布直方图的情况会有什么变化?假如增至10000呢?总体密度曲线月均用水量/tab (图中阴影部分的面积,表示总体在某个区间 (a, b) 内取值的百分比)。引入:某篮球运动员在某赛季各场比赛的得分情况如下:
12,15,24,25,31,31,36,37,39,44,49,50.问题1:如何分析该运动员的整体水平及发挥的稳定程度?问题2:初中统计部分曾学过用什么来反映总体的水平?用什么来考察稳定程度? 用样本分布直方图去估计相应的总体分布时,一般样本容量越大,频率分布直方图就会无限接近总体密度曲线,就越精确地反映了总体的分布规律,即越精确地反映了总体在各个范围内取值百分比。 总体密度曲线反映了总体在各个范围内取值的百分比,精确地反映了总体的分布规律。是研究总体分布的工具.总体密度曲线 在初中我们学过用平均数、众数和中位数反映总体的水平,用方差考察稳定程度。 我们还有一种简易的方法,就是将这些数据有条理的列出来,从中观察数据的分布情况,这种方法就是我们今天要学习的茎叶图。制作茎叶图的方法是:将所有两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出.茎叶图的制作方法注意:在制作茎叶图时,重复出现的数据要重复记录,不能遗漏,特别是“叶”部分;同一数据出现几次,就要在图中体现几次.茎叶图某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:(1)甲运动员得分:
13,51,23,8,26,38,16,33,14,28,39(1)乙运动员得分: 49,24,12,31,50,31,44,36,15,37,25,36,39茎叶图甲乙0
1
2
3
4
5
2 5
5 4
1 6 1 6 7 9
4 9
08
4 6 3
6 8
3 8 9
1 叶就是从茎的旁边生长出来的数,表示得分的个位数。 茎是指中间的一列数,表示得分的十位数茎叶图的特征
1.用茎叶图表示数据有两个优点:一是从统计图
上没有原始数据信息的损失,所有数据信息都可
以从茎叶图中得到;二是茎叶图中的数据可以随
时记录,随时添加,方便记录与表示。
2.茎叶图只便于表示两位有效数字的数据,而且
茎叶图只方便记录两组的数据,两个以上的数据
虽然能够记录,但是没有表示两个记录那么直观、
清晰。分析:茎是指中间的一列数,叶就是从茎的旁
边生长出来的数。中间的数字表示得分的十位
数,旁边的数字分别表示两个人得分的个位数。
乙运动员的得分基本上是对称的,叶的分布是
“单峰”的,有的叶集中在茎2,3,4上,中位数
是36;甲运动员的得分除一个特殊得分(51分)
外,也大致对称,叶的分布也是“单峰”的,的叶
集中在茎1,2,3上,中位数是26。由此可看出,
乙运动员的成绩更好。另外,从叶在茎上的分布
情况看,乙运动员的得分集中于峰值附近,这说
明乙运动员的发挥更稳定.例3. 某中学高一(2) 班甲、乙两名同学自高中
以来每场数学考试成绩情况如下:
甲的得分:95,81,75,91,86,89,71,65,76,
88,94,110,107;
乙的得分:83,86,93,99,88,103,98,114,
98,79,101.
画出两人数学成绩的茎叶图,请根据茎叶图对
两人的成绩进行比较.分析:用中间的数字表示两位同学得分的十位数和
百位数.两边的数字分别表示两人每场数学考试成
绩的个位数.解:甲、乙两人数学成绩的茎叶图如下图. 从这个茎叶图上可以看出 乙同学的得分情况是大
致对称的,中位数是98;甲同学的得分情况除一个特殊
得分(110分)外. 也大致对称,中位数是88.因此乙
同学发挥比较稳定,总体得分情况比甲同学好. 例题4:有一个容量为50的样本,其数
据的茎叶图表示如下:
茎 叶
1 34566678888999
2 0000112222233334455566667778889
3 01123
将其分成7组并要求:
(1)列出样本的频率分布表;
(2)画出频率分布直方图以及频率分布折线图. 1.一次选拔运动员,测得7名选手的身高(单位:cm)分布茎叶图如图,记录的平均身高为177 cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为( )
A.5 B.6
C.7 D.8
解析:选D.由题意可知,3+4-7-4+(x-7)+1+2=0,解得x=8.随堂练习2.甲、乙两位同学某学科的连续五次考试成绩用茎叶图表示如右:则平均分数较高的是__________,成绩较为稳定的是__________.
答案:甲 甲随堂练习巩固练习:
1、甲、乙两篮球运动员上赛季每场比赛的得分如下,
甲 12,15,24,25,31,31,36,36,37,39,44,49,50
乙 8,13,14,16,23,26,28,33,
38,39,51
试用茎叶图将这些数据列出来,观察数据的分布情况,比较这两位运动员的得分水平.
2.下面是甲、乙两名运动员某赛季一些场次得分的茎叶图:(1)甲,乙两名队员的
最高得分各是多少?(2)哪名运动员
的成绩好一些?3.有一个容量为50的样本,其数据的茎叶图表示如下:
?
?
?
?
?
将其分成7组并要求:
(1)列出样本的频率分布表;
(2)画出频率分布直方图以及密度曲线 1
2
3
34566678888999
0000112222233334455566667778889
01123
作业:
P71练习:3.
P81习题2.2 A组:
1.(1)(2)(3).
