北师大版七下数学 第二章 平行线的性质和判定 复习课 教案
文档属性
| 名称 | 北师大版七下数学 第二章 平行线的性质和判定 复习课 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 48.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 10:34:06 | ||
图片预览

文档简介
平行线的判定和性质复习课
一、 教学目标
1、通过平行线判定和性质的简单练习,进一步让学生感受平行线判定方法与平行线性质的区别和联系,并能正确掌握和解决平行线性质和判定的一般问题。
2、通过在数学过程中安排一定时间思考和交流,进一步认识平行线判定方法与平行线性质的区别和联系,提高分析问题、解决问题的能力、几何语言的书写和表达能力,为了今后平面几何的学习打下坚实的基础。
3、利用平行线的判定和性质,进一步体会几何说理过程,通过学生实践操作,和对例题的题意和变式的分析、讨论,让学生一起参与协作学习,感受集体主义精神,同时提供尝试成功的空间,进一步激发学生学习积极性。
二、教学重点、难点
重点: 理解并掌握平行线判定和性质之间的区别与联系。
难点: 通过例题和例题的变式练习,提高平行线判定和性质的综合运用能力。
三、教材分析
《平行线的判定和性质》是上海教育出版社七年级《数学》第十三章的内容。本章的知识内容是平面几何的奠基和入门,要求学生正确认识几何概念,掌握知识之间的基本联系和基本运用,具有初步的逻辑推理意识、语言表达能力,言必有据的习惯。会依据平行线的判断和性质及其有关基本事实进行说理,初步感知逻辑推理的过程及其表达。
学情分析
七年级学生的理解能力和抽象思维能力都比较弱,对于平面图形停留在直观感觉上。根据学生的这种情况,我通过简单的小练习,积极引导和有效促进学生落实本章学习的基本要求。学生在学习几何中,在直观感知、逻辑分析、数学思考和规范表达等方面面临一定的困难,容易出现各种各样的问题,所以要通过课堂活动,引导学生重视画图、重视讲理和言必有据,正确、简明、有条理地表达。同时运用多媒体手段,把原本抽象枯燥的几何问题变成形象直观、有趣的活动,有效地调动了学生的主观能动性,使学生从被动学习转变为主动探究学习。
五、教学过程
教学过程 内容、方法、活动 设计意图
(1)温故知新 1、判定两条直线平行有哪些方法?在这些方法中,已经知道了什么?得到的结果是什么?平行线的判定:① 同位角相等,两直线平行② 内错角相等,两直线平行③ 同旁内角互补,两直线平行2、已知两条直线平行,那么同位角,内错角,同旁内角间有什么关系?平行线的性质:①两直线平行,同位角相等②两直线平行,内错角相等 ③两直线平行,同旁内角互补 总结: 性质两直线平行 判定由“角的关系”得到“两直线平行”的结论是“平行线的判定”用途:说明直线平行由“两直线平行””得到“角的关系”的结论是“平行线的性质”用途:说明角相等或互补 温故知新,复习旧知,引入复习课的知识要点。让学生感受平行线性质与平行线判定方法的区别和联系。
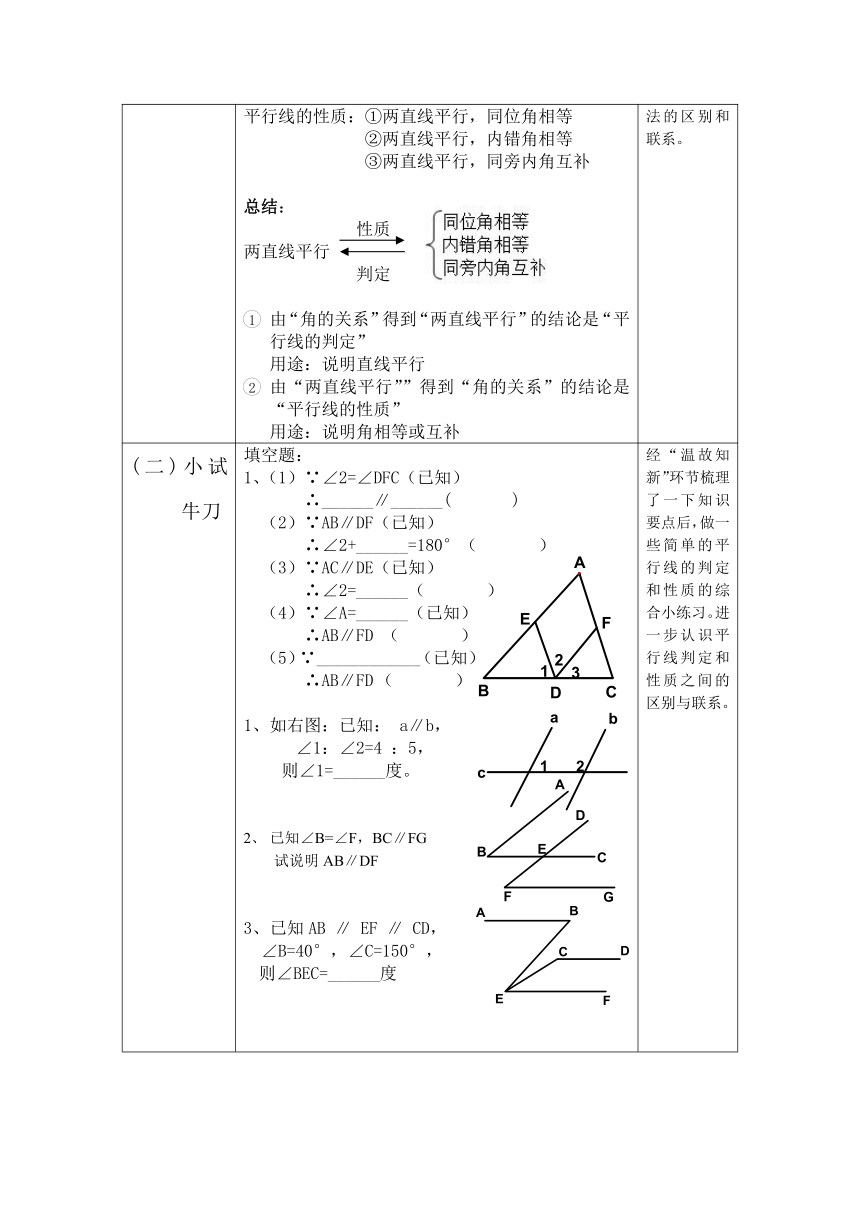
(二)小试牛刀 填空题:1、(1)∵∠2=∠DFC(已知) ∴______∥______( )(2)∵AB∥DF(已知)∴∠2+______=180°( )(3)∵AC∥DE(已知)∴∠2=______( )(4)∵∠A=______(已知)∴AB∥FD ( )(5)∵____________(已知)∴AB∥FD ( )1、如右图:已知: a∥b,∠1:∠2=4 :5,则∠1=______度。已知∠B=∠F,BC∥FG试说明AB∥DF3、已知AB ∥ EF ∥ CD, ∠B=40°,∠C=150°,则∠BEC=______度 经“温故知新”环节梳理了一下知识要点后,做一些简单的平行线的判定和性质的综合小练习。进一步认识平行线判定和性质之间的区别与联系。
(三)例题精讲 例1:如图所示:点D为AE上的点,点B为FC上的点,AE∥FC,∠A=∠C,试说明AB∥DC解: ∵ AD//BC(已知)∴ ∠A=∠ABF(两直线平行,内错角相等)又∵∠A=∠C (已知)∴ ∠ABF=∠C(等量代换)∴ AB∥DC(同位角相等,两直线平行)想一想:有多少种说明平行的方法呢?那如例1中,如果已知AB∥DC,∠A=∠C,那能说明AE∥FC吗?变式1:如图所示:点D为AE上的点,点B为FC上的点,AB∥DC,∠A=∠C,试说明 AE∥FC 解:∵ AB//DC(已知)∴ ∠C=∠ABF(两直线平行,同位角相等)又∵∠A=∠C (已知)∴ ∠ABF=∠A(等量代换)∴ AE∥FC(内错角相等,两直线平行)变式2:如图,点D为AE上的点,点B为FC上的点,∠1= ∠2, ∠C= ∠A,求证:AE ∥FC解:∵∠1=∠2 (已知)∠1=∠3 (对顶角相等)∴ ∠2=∠3(等量代换)∴ AB∥CD(同位角相等,两直线平行)∴ ∠C=∠ABF(两直线平行,同位角相等)又∵∠C=∠A (已知)∴ ∠A=∠ABF (等量代换)∴ AE∥FC(内错角相等,两直线平行)变式3:如图,已知∠E=∠F,∠C=∠A,试着说明AB//CD解:∵∠E=∠F(已知)∴ AE∥FC(内错角相等,两直线平行)∴ ∠A=∠ABF (两直线平行,内错角相等)又∵∠C=∠A (已知)∴ ∠C=∠ABF(等量代换)∴ AB∥CD(同位角相等,两直线平行)例2:已知:如图:BD平分∠ ABC ① ∠1=∠2 ,∠C=70②。求∠ADE 的度数③。 解:∵ BD平分∠ ABC(已知)∴∠1=∠DBC(角平分线的意义)∵∠1=∠2(已知)∴∠2=∠DBC(等量代换)∴ ED∥BC(内错角相等, 两直线平行)∴∠C=∠ADE(两直线平行,同位角相等)又∵∠C=70°(已知)∴∠C=∠ADE= 70°(等量代换)变式1:已知:如图:∠1=∠2 , ∠ C=70, ∠ADE =70°问 BD平分∠ABC吗?解:∵∠ C=70,∠ADE =70°(已知)∴ ∠ADE= ∠C(等量代换)∴DE∥ BC(同位角相等,两直线平行)∴∠2=∠DBC(两直线平行,内错角相等)又∵∠1= ∠2(已知)∴ ∠1= ∠DBC(等量代换)∴ BD平分∠ABC(角平分线的意义) 由例1引出,变式1,2,3。理解一题多解的思想。培养逻辑思维能力,“举一反三”的能力。拒绝题海战,达到一道题目,多角度思考的能力。让学生自主学习,分别把3个条件分为①②③,由例2,我们可以知道,用条件①②可以推出③。让学生自主思考用条件②③可以推出①吗?试说明理由。
(四)课堂小结 这节课你有什么收获吗?使用判定定理时是,已知“角的相等或互补”说明“两直线平行” 归纳:由“角”定“线”使用性质定理时是,已知“两直线平行”说明“角的相等或互补” 归纳:由“线”定“角” 通过小结,梳理一节课的收获,培养学生的归纳能力。
作业布置:补充练习题
作业反馈:
教学反思:
一、 教学目标
1、通过平行线判定和性质的简单练习,进一步让学生感受平行线判定方法与平行线性质的区别和联系,并能正确掌握和解决平行线性质和判定的一般问题。
2、通过在数学过程中安排一定时间思考和交流,进一步认识平行线判定方法与平行线性质的区别和联系,提高分析问题、解决问题的能力、几何语言的书写和表达能力,为了今后平面几何的学习打下坚实的基础。
3、利用平行线的判定和性质,进一步体会几何说理过程,通过学生实践操作,和对例题的题意和变式的分析、讨论,让学生一起参与协作学习,感受集体主义精神,同时提供尝试成功的空间,进一步激发学生学习积极性。
二、教学重点、难点
重点: 理解并掌握平行线判定和性质之间的区别与联系。
难点: 通过例题和例题的变式练习,提高平行线判定和性质的综合运用能力。
三、教材分析
《平行线的判定和性质》是上海教育出版社七年级《数学》第十三章的内容。本章的知识内容是平面几何的奠基和入门,要求学生正确认识几何概念,掌握知识之间的基本联系和基本运用,具有初步的逻辑推理意识、语言表达能力,言必有据的习惯。会依据平行线的判断和性质及其有关基本事实进行说理,初步感知逻辑推理的过程及其表达。
学情分析
七年级学生的理解能力和抽象思维能力都比较弱,对于平面图形停留在直观感觉上。根据学生的这种情况,我通过简单的小练习,积极引导和有效促进学生落实本章学习的基本要求。学生在学习几何中,在直观感知、逻辑分析、数学思考和规范表达等方面面临一定的困难,容易出现各种各样的问题,所以要通过课堂活动,引导学生重视画图、重视讲理和言必有据,正确、简明、有条理地表达。同时运用多媒体手段,把原本抽象枯燥的几何问题变成形象直观、有趣的活动,有效地调动了学生的主观能动性,使学生从被动学习转变为主动探究学习。
五、教学过程
教学过程 内容、方法、活动 设计意图
(1)温故知新 1、判定两条直线平行有哪些方法?在这些方法中,已经知道了什么?得到的结果是什么?平行线的判定:① 同位角相等,两直线平行② 内错角相等,两直线平行③ 同旁内角互补,两直线平行2、已知两条直线平行,那么同位角,内错角,同旁内角间有什么关系?平行线的性质:①两直线平行,同位角相等②两直线平行,内错角相等 ③两直线平行,同旁内角互补 总结: 性质两直线平行 判定由“角的关系”得到“两直线平行”的结论是“平行线的判定”用途:说明直线平行由“两直线平行””得到“角的关系”的结论是“平行线的性质”用途:说明角相等或互补 温故知新,复习旧知,引入复习课的知识要点。让学生感受平行线性质与平行线判定方法的区别和联系。
(二)小试牛刀 填空题:1、(1)∵∠2=∠DFC(已知) ∴______∥______( )(2)∵AB∥DF(已知)∴∠2+______=180°( )(3)∵AC∥DE(已知)∴∠2=______( )(4)∵∠A=______(已知)∴AB∥FD ( )(5)∵____________(已知)∴AB∥FD ( )1、如右图:已知: a∥b,∠1:∠2=4 :5,则∠1=______度。已知∠B=∠F,BC∥FG试说明AB∥DF3、已知AB ∥ EF ∥ CD, ∠B=40°,∠C=150°,则∠BEC=______度 经“温故知新”环节梳理了一下知识要点后,做一些简单的平行线的判定和性质的综合小练习。进一步认识平行线判定和性质之间的区别与联系。
(三)例题精讲 例1:如图所示:点D为AE上的点,点B为FC上的点,AE∥FC,∠A=∠C,试说明AB∥DC解: ∵ AD//BC(已知)∴ ∠A=∠ABF(两直线平行,内错角相等)又∵∠A=∠C (已知)∴ ∠ABF=∠C(等量代换)∴ AB∥DC(同位角相等,两直线平行)想一想:有多少种说明平行的方法呢?那如例1中,如果已知AB∥DC,∠A=∠C,那能说明AE∥FC吗?变式1:如图所示:点D为AE上的点,点B为FC上的点,AB∥DC,∠A=∠C,试说明 AE∥FC 解:∵ AB//DC(已知)∴ ∠C=∠ABF(两直线平行,同位角相等)又∵∠A=∠C (已知)∴ ∠ABF=∠A(等量代换)∴ AE∥FC(内错角相等,两直线平行)变式2:如图,点D为AE上的点,点B为FC上的点,∠1= ∠2, ∠C= ∠A,求证:AE ∥FC解:∵∠1=∠2 (已知)∠1=∠3 (对顶角相等)∴ ∠2=∠3(等量代换)∴ AB∥CD(同位角相等,两直线平行)∴ ∠C=∠ABF(两直线平行,同位角相等)又∵∠C=∠A (已知)∴ ∠A=∠ABF (等量代换)∴ AE∥FC(内错角相等,两直线平行)变式3:如图,已知∠E=∠F,∠C=∠A,试着说明AB//CD解:∵∠E=∠F(已知)∴ AE∥FC(内错角相等,两直线平行)∴ ∠A=∠ABF (两直线平行,内错角相等)又∵∠C=∠A (已知)∴ ∠C=∠ABF(等量代换)∴ AB∥CD(同位角相等,两直线平行)例2:已知:如图:BD平分∠ ABC ① ∠1=∠2 ,∠C=70②。求∠ADE 的度数③。 解:∵ BD平分∠ ABC(已知)∴∠1=∠DBC(角平分线的意义)∵∠1=∠2(已知)∴∠2=∠DBC(等量代换)∴ ED∥BC(内错角相等, 两直线平行)∴∠C=∠ADE(两直线平行,同位角相等)又∵∠C=70°(已知)∴∠C=∠ADE= 70°(等量代换)变式1:已知:如图:∠1=∠2 , ∠ C=70, ∠ADE =70°问 BD平分∠ABC吗?解:∵∠ C=70,∠ADE =70°(已知)∴ ∠ADE= ∠C(等量代换)∴DE∥ BC(同位角相等,两直线平行)∴∠2=∠DBC(两直线平行,内错角相等)又∵∠1= ∠2(已知)∴ ∠1= ∠DBC(等量代换)∴ BD平分∠ABC(角平分线的意义) 由例1引出,变式1,2,3。理解一题多解的思想。培养逻辑思维能力,“举一反三”的能力。拒绝题海战,达到一道题目,多角度思考的能力。让学生自主学习,分别把3个条件分为①②③,由例2,我们可以知道,用条件①②可以推出③。让学生自主思考用条件②③可以推出①吗?试说明理由。
(四)课堂小结 这节课你有什么收获吗?使用判定定理时是,已知“角的相等或互补”说明“两直线平行” 归纳:由“角”定“线”使用性质定理时是,已知“两直线平行”说明“角的相等或互补” 归纳:由“线”定“角” 通过小结,梳理一节课的收获,培养学生的归纳能力。
作业布置:补充练习题
作业反馈:
教学反思:
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
