2021-2022学年鲁科版选择性必修2第2节洛伦兹力 作业(解析版)
文档属性
| 名称 | 2021-2022学年鲁科版选择性必修2第2节洛伦兹力 作业(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-04 09:46:24 | ||
图片预览




文档简介
第2节 洛伦兹力
一、单选题
1.如图所示,圆形区域内有垂直纸面的匀强磁场,三个质量和电荷量相同的带电粒子a、b、c,以不同的速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图。若带电粒子只受磁场力的作用。则下列说法正确的是( )
A.a粒子动能最大
B.c粒子速率最大
C.b粒子在磁场中运动时间最长
D.它们做圆周运动的周期Ta2.我国提供永磁体的阿尔法磁谱仪(下图是它的原理图)由航天飞机携带升空并安装在国际空间站中,它的主要使命之一是探索宇宙中的反物质。所谓反物质,就是质量与正粒子相等、电荷量与正粒子相等但电性相反的粒子。假如使一束质子、反质子、粒子(核)和反粒子组成的射线,以相同的速度大小沿通过匀强磁场进入匀强磁场而形成图中的4条径迹,则( )
A.1、3是反粒子径迹 B.2为反质子径迹
C.1、2为反粒子径迹 D.3为粒子径迹
3.如图所示,真空中一束电子沿一螺线管轴线进入管内。不计电子所受的重力,以下关于电子在螺线管内运动情况的描述中正确的是( )
A.当从a端通入电流时,电子做匀加速直线运动
B.当从b端通入电流时,电子做匀加速直线运动
C.不管从哪端通入电流,电子都做匀速直线运动
D.不管从哪端通入电流,电子都做匀速圆周运动
4.如图所示,MN的右侧存在范围足够大、磁感应强度大小为B的匀强磁场,磁场方向垂直纸面向里,MN右侧到MN的距离为L的O处有一个粒子源,可沿纸面内各个方向射出质量为m、电荷量为q的带正电粒子(不计重力及粒子间的相互作用),速度均为,则粒子在磁场中运动的最短时间为( )
A. B. C. D.
5.如图所示,在x轴上方存在垂直于纸面向里的足够宽的匀强磁场,磁感应强度为B。在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计)。则下列说法正确的是( )
A.若v一定,θ越大,则粒子在磁场中运动的时间越短
B.若v一定,θ越大,则粒子在离开磁场的位置距O点越远
C.若θ一定,v越大,则粒子在磁场中运动的角速度越大
D.若θ一定,v越大,则粒子在磁场中运动的时间越短
6.处于匀强磁场中的一个带电粒子,仅在磁场力作用下做匀速圆周运动。该粒子的运动可与环形电流等效,此等效电流( )
A.与粒子的电荷量成正比 B.与粒子的速度大小成正比
C.与粒子的质量成正比 D.与匀强磁场的磁感应强度大小成正比
7.质量为m、电荷量为q的小物块,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向里的匀强磁场中,磁感应强度为B,如图所示。若带电小物块下滑后某时刻对斜面的作用力恰好为零,下面说法中正确的是( )
A.小物块一定带正电
B.小物块在斜面上运动时做匀加速直线运动
C.小物块在斜面上运动时做加速度增大、而速度也增大的变加速直线运动
D.小物块在斜面上下滑过程中,当小物块对斜面压力为零时的速率为
8.如图所示,摆球上带有负电的单摆,在一匀强磁场中摆动,匀强磁场的方向垂直于纸面向里,摆球在A、间摆动过程中,由A摆到最低点时,摆线拉力大小为,摆球加速度大小为;由摆到最低点时,摆线拉力大小为,摆球加速度大小为,则( )
A., B.,
C., D.,
9.如图所示,a和b是从A点以相同的速度垂直磁场方向射入匀强磁场的两个粒子运动的半圆形轨迹,已知两个粒子带电荷量相同,且,不计重力的影响,则由此可知( )
A.两粒子均带正电,质量之比
B.两粒子均带负电,质量之比
C.两粒子均带正电,质量之比
D.两粒子均带负电,质量之比
10.如图所示,有界匀强磁场边界线SP∥MN,速率不同的同种带电粒子从S点沿SP方向同时射入磁场。其中穿过a点的粒子的速率v1与MN垂直;穿过b点的粒子的速率v2与MN成60°角,设两粒子从S点到a、b两点所需时间分别为t1和t2,则t1∶t2为(粒子的重力不计)( )
A.1∶3 B.4∶3 C.1∶1 D.3∶2
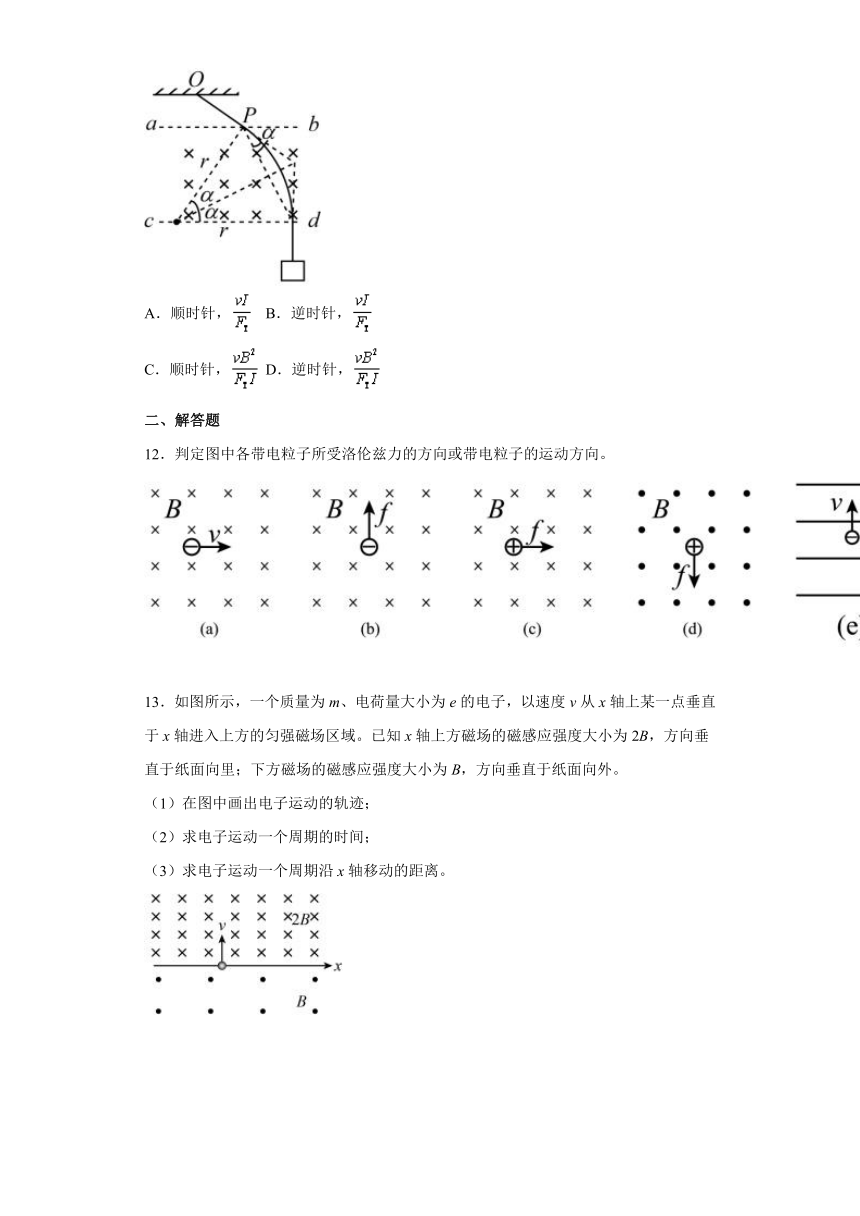
11.物理学家有时用通电软导线模拟粒子在磁场中的运动轨迹。如图所示,ab、cd两平行直线为匀强磁场的理想边界,磁场方向垂直纸面向里,磁感应强度为B,一轻质软导线一端固定于O点,另一端悬挂一重物。当软导线通以电流I时,重物使软导线中产生张力FT,软导线形成一段圆弧,导线OP与圆弧相切于P点(导线与ab的交点)。撤去软导线,通过P点沿原来OP方向射入速度为v的带电粒子,粒子将沿同一圆弧运动。则导线中的电流方向及带电粒子的比荷分别为( )
A.顺时针, B.逆时针,
C.顺时针, D.逆时针,
二、解答题
12.判定图中各带电粒子所受洛伦兹力的方向或带电粒子的运动方向。
13.如图所示,一个质量为m、电荷量大小为e的电子,以速度v从x轴上某一点垂直于x轴进入上方的匀强磁场区域。已知x轴上方磁场的磁感应强度大小为2B,方向垂直于纸面向里;下方磁场的磁感应强度大小为B,方向垂直于纸面向外。
(1)在图中画出电子运动的轨迹;
(2)求电子运动一个周期的时间;
(3)求电子运动一个周期沿x轴移动的距离。
参考答案:
1.B
【解析】设粒子的电荷量和质量分别为q和m,速率为v,根据牛顿第二定律有
解得
粒子运动的周期为
粒子在磁场中运动时间为
由题图可知c粒子运动半径最大,速率最大,动能最大;a粒子转过的圆心角最大,在磁场中运动的时间最长;三个粒子做圆周运动的周期相等。综上所述可知ACD错误,B正确。
故选B。
2.C
【解析】在磁场中,粒子做匀速圆周运动,正离子受力向右,向右偏转;负离子向左偏转。故1、2为反粒子径迹;
根据洛伦兹力提供向心力有
解得:
故质子与α粒子的半径之比为1:2,即α粒子转弯半径大,所以3是质子,4是α粒子;1是反质子,2是反α粒子;
故选C。
3.C
【解析】根据安培定则知不管那端通入电流,螺线管中产生的磁场方向平行于螺线管的中心轴线,则电子的运动方向与磁场方向平行,电子不受洛仑兹力,做匀速直线运动。
故选C。
4.B
【解析】由洛伦兹力提供向心力可得
v=
所以粒子在磁场中运动的半径为
r==L
粒子在磁场中运动时间最短,对应的弧长最短、弦长最短,由几何关系得,当弦长等于L时最短,此时弦切角为30°,圆心角为60°,如图所示,运动的最短时间是
tmin=T=×=
ACD错误,故B正确。
故选B。
5.A
【解析】AB.正粒子从磁场边界入射做匀速圆周运动,洛仑兹力提供向心力,有
从而
当θ为锐角时,画出正粒子运动轨迹如图所示
由几何关系可知,入射点与出射点
而粒子在磁场的运动时间
与速度无关;
当θ为钝角时,画出正粒子运动轨迹如图所示
由几何关系入射点与出射点
而粒子在磁场中运动时间
与第一种情况相同,则若v一定,θ越大,从时间公式可以看出运动时间越短;
若v一定,θ为锐角越大时,则Oa就越大,但θ为钝角越大时,由上式可以看出Oa不一定越远,故A正确,B错误;
C.由
可得粒子运动的角速度
显然与速度无关,故C错误;
D.运动时间无论是锐角还是钝角,时间均为
与速度无关,即若θ一定,无论v大小如何,则粒子在磁场中运动的时间都保持不变,故D错误。
故选A。
6.D
【解析】粒子在磁场中做匀速圆周运动
得
又
而
联立解得
由此可知等效电流与粒子速率无关,与粒子电荷量的平方成正比,与粒子质量成反比,与磁感应强度成正比,故D正确,ABC错误。
故选D。
7.B
【解析】A.带电小物块下滑后某时刻对斜面的作用力恰好为零,知其所受洛伦兹力的方向应垂直于斜面向上,根据左手定则知,小物块带负电,故A错误;
BC.小物块在运动的过程中受重力、斜面的支持力和洛伦兹力,合力沿斜面向下,大小为
根据牛顿第二定律知
小物块在斜面上运动时做匀加速直线运动,故B正确,C错误;
D.当压力为零时,在垂直于斜面方向上的合力为零,有
解得
故D错误。
故选B。
8.B
【解析】CD.由于洛伦兹力不做功,所以摆球由到达和由A到达的速度大小相等,由
可得
故CD错误。
AB.当由A运动到时,以摆球为研究对象,受力分析如图甲所示
当由运动到时,受力分析如图乙所示
因此
故A错误,B正确。
故选B。
9.B
【解析】AC.两粒子进入磁场后均向下偏转,可知在A点均受到向下的洛伦兹力,由左手定则可知,两个粒子均带负电,AC错误;
BD.在磁场中由洛伦兹力提供向心力,则有
得
因两粒子进入磁场的速度相同,电荷量也相同,又在同一磁场中运动,故
B正确,D错误。
故选B。
10.D
【解析】如图所示
可求出从a点射出的粒子对应的圆心角为90°,从b点射出的粒子对应的圆心角为60°,由
式中为圆心角,可得
故D正确。
故选D。
11.A
【解析】如图所示,设圆弧的弦切角为α,弦长为l,由几何知识有
l=2rsinα
对导线分析受力,由平衡条件可得,导线所受安培力斜向右上方,则导线中的电流方向沿顺时针,且
2FTsinα=IlB
解得
对带电粒子,由洛伦兹力提供向心力有
解得
故A正确,BCD错误。
故选A。
12.(a)粒子受力方向为垂直速度向下;(b)粒子运动方向为垂直力的方向向左;(c)粒子运动方向为垂直力的方向向下;(d)粒子运动方向为垂直力的方向向右;(e)粒子受力方向为垂直纸面向外。
【解析】(a)粒子带负电,向右运动,根据左手定则判断粒子受力方向为垂直速度向下;
(b)粒子带负电,受力向上,根据左手定则,四指指向右,所以粒子运动方向为垂直力的方向向左;
(c)粒子带正电,受力向右,根据左手定则,四指指向下,所以粒子运动方向为垂直力的方向向下;
(d)粒子带正电,受力向下,根据左手定则,四指指向右,所以粒子运动方向为垂直力的方向向右;
(e)粒子带负电,向上运动,根据左手定则,大拇指指向外,所以粒子受力方向为垂直纸面向外。
13.(1) ;(2);(3)
【解析】(1)电子轨迹如图所示
(2)电子在上方磁场运动的周期
电子在下方磁场运动的周期
在一个周期内,电子在上方磁场运动轨迹为一个半圆,下方磁场运动轨迹为半圆,故电子运动一个周期的时间
(3)设电子在上方磁场做圆周运动的半径为R1,下方磁场做圆周运动的半径为R2,由牛顿第二定律
由几何关系知,电子运动一个周期沿x轴移动的距离
联立知
一、单选题
1.如图所示,圆形区域内有垂直纸面的匀强磁场,三个质量和电荷量相同的带电粒子a、b、c,以不同的速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图。若带电粒子只受磁场力的作用。则下列说法正确的是( )
A.a粒子动能最大
B.c粒子速率最大
C.b粒子在磁场中运动时间最长
D.它们做圆周运动的周期Ta
A.1、3是反粒子径迹 B.2为反质子径迹
C.1、2为反粒子径迹 D.3为粒子径迹
3.如图所示,真空中一束电子沿一螺线管轴线进入管内。不计电子所受的重力,以下关于电子在螺线管内运动情况的描述中正确的是( )
A.当从a端通入电流时,电子做匀加速直线运动
B.当从b端通入电流时,电子做匀加速直线运动
C.不管从哪端通入电流,电子都做匀速直线运动
D.不管从哪端通入电流,电子都做匀速圆周运动
4.如图所示,MN的右侧存在范围足够大、磁感应强度大小为B的匀强磁场,磁场方向垂直纸面向里,MN右侧到MN的距离为L的O处有一个粒子源,可沿纸面内各个方向射出质量为m、电荷量为q的带正电粒子(不计重力及粒子间的相互作用),速度均为,则粒子在磁场中运动的最短时间为( )
A. B. C. D.
5.如图所示,在x轴上方存在垂直于纸面向里的足够宽的匀强磁场,磁感应强度为B。在xOy平面内,从原点O处沿与x轴正方向成θ角(0<θ<π)以速率v发射一个带正电的粒子(重力不计)。则下列说法正确的是( )
A.若v一定,θ越大,则粒子在磁场中运动的时间越短
B.若v一定,θ越大,则粒子在离开磁场的位置距O点越远
C.若θ一定,v越大,则粒子在磁场中运动的角速度越大
D.若θ一定,v越大,则粒子在磁场中运动的时间越短
6.处于匀强磁场中的一个带电粒子,仅在磁场力作用下做匀速圆周运动。该粒子的运动可与环形电流等效,此等效电流( )
A.与粒子的电荷量成正比 B.与粒子的速度大小成正比
C.与粒子的质量成正比 D.与匀强磁场的磁感应强度大小成正比
7.质量为m、电荷量为q的小物块,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向里的匀强磁场中,磁感应强度为B,如图所示。若带电小物块下滑后某时刻对斜面的作用力恰好为零,下面说法中正确的是( )
A.小物块一定带正电
B.小物块在斜面上运动时做匀加速直线运动
C.小物块在斜面上运动时做加速度增大、而速度也增大的变加速直线运动
D.小物块在斜面上下滑过程中,当小物块对斜面压力为零时的速率为
8.如图所示,摆球上带有负电的单摆,在一匀强磁场中摆动,匀强磁场的方向垂直于纸面向里,摆球在A、间摆动过程中,由A摆到最低点时,摆线拉力大小为,摆球加速度大小为;由摆到最低点时,摆线拉力大小为,摆球加速度大小为,则( )
A., B.,
C., D.,
9.如图所示,a和b是从A点以相同的速度垂直磁场方向射入匀强磁场的两个粒子运动的半圆形轨迹,已知两个粒子带电荷量相同,且,不计重力的影响,则由此可知( )
A.两粒子均带正电,质量之比
B.两粒子均带负电,质量之比
C.两粒子均带正电,质量之比
D.两粒子均带负电,质量之比
10.如图所示,有界匀强磁场边界线SP∥MN,速率不同的同种带电粒子从S点沿SP方向同时射入磁场。其中穿过a点的粒子的速率v1与MN垂直;穿过b点的粒子的速率v2与MN成60°角,设两粒子从S点到a、b两点所需时间分别为t1和t2,则t1∶t2为(粒子的重力不计)( )
A.1∶3 B.4∶3 C.1∶1 D.3∶2
11.物理学家有时用通电软导线模拟粒子在磁场中的运动轨迹。如图所示,ab、cd两平行直线为匀强磁场的理想边界,磁场方向垂直纸面向里,磁感应强度为B,一轻质软导线一端固定于O点,另一端悬挂一重物。当软导线通以电流I时,重物使软导线中产生张力FT,软导线形成一段圆弧,导线OP与圆弧相切于P点(导线与ab的交点)。撤去软导线,通过P点沿原来OP方向射入速度为v的带电粒子,粒子将沿同一圆弧运动。则导线中的电流方向及带电粒子的比荷分别为( )
A.顺时针, B.逆时针,
C.顺时针, D.逆时针,
二、解答题
12.判定图中各带电粒子所受洛伦兹力的方向或带电粒子的运动方向。
13.如图所示,一个质量为m、电荷量大小为e的电子,以速度v从x轴上某一点垂直于x轴进入上方的匀强磁场区域。已知x轴上方磁场的磁感应强度大小为2B,方向垂直于纸面向里;下方磁场的磁感应强度大小为B,方向垂直于纸面向外。
(1)在图中画出电子运动的轨迹;
(2)求电子运动一个周期的时间;
(3)求电子运动一个周期沿x轴移动的距离。
参考答案:
1.B
【解析】设粒子的电荷量和质量分别为q和m,速率为v,根据牛顿第二定律有
解得
粒子运动的周期为
粒子在磁场中运动时间为
由题图可知c粒子运动半径最大,速率最大,动能最大;a粒子转过的圆心角最大,在磁场中运动的时间最长;三个粒子做圆周运动的周期相等。综上所述可知ACD错误,B正确。
故选B。
2.C
【解析】在磁场中,粒子做匀速圆周运动,正离子受力向右,向右偏转;负离子向左偏转。故1、2为反粒子径迹;
根据洛伦兹力提供向心力有
解得:
故质子与α粒子的半径之比为1:2,即α粒子转弯半径大,所以3是质子,4是α粒子;1是反质子,2是反α粒子;
故选C。
3.C
【解析】根据安培定则知不管那端通入电流,螺线管中产生的磁场方向平行于螺线管的中心轴线,则电子的运动方向与磁场方向平行,电子不受洛仑兹力,做匀速直线运动。
故选C。
4.B
【解析】由洛伦兹力提供向心力可得
v=
所以粒子在磁场中运动的半径为
r==L
粒子在磁场中运动时间最短,对应的弧长最短、弦长最短,由几何关系得,当弦长等于L时最短,此时弦切角为30°,圆心角为60°,如图所示,运动的最短时间是
tmin=T=×=
ACD错误,故B正确。
故选B。
5.A
【解析】AB.正粒子从磁场边界入射做匀速圆周运动,洛仑兹力提供向心力,有
从而
当θ为锐角时,画出正粒子运动轨迹如图所示
由几何关系可知,入射点与出射点
而粒子在磁场的运动时间
与速度无关;
当θ为钝角时,画出正粒子运动轨迹如图所示
由几何关系入射点与出射点
而粒子在磁场中运动时间
与第一种情况相同,则若v一定,θ越大,从时间公式可以看出运动时间越短;
若v一定,θ为锐角越大时,则Oa就越大,但θ为钝角越大时,由上式可以看出Oa不一定越远,故A正确,B错误;
C.由
可得粒子运动的角速度
显然与速度无关,故C错误;
D.运动时间无论是锐角还是钝角,时间均为
与速度无关,即若θ一定,无论v大小如何,则粒子在磁场中运动的时间都保持不变,故D错误。
故选A。
6.D
【解析】粒子在磁场中做匀速圆周运动
得
又
而
联立解得
由此可知等效电流与粒子速率无关,与粒子电荷量的平方成正比,与粒子质量成反比,与磁感应强度成正比,故D正确,ABC错误。
故选D。
7.B
【解析】A.带电小物块下滑后某时刻对斜面的作用力恰好为零,知其所受洛伦兹力的方向应垂直于斜面向上,根据左手定则知,小物块带负电,故A错误;
BC.小物块在运动的过程中受重力、斜面的支持力和洛伦兹力,合力沿斜面向下,大小为
根据牛顿第二定律知
小物块在斜面上运动时做匀加速直线运动,故B正确,C错误;
D.当压力为零时,在垂直于斜面方向上的合力为零,有
解得
故D错误。
故选B。
8.B
【解析】CD.由于洛伦兹力不做功,所以摆球由到达和由A到达的速度大小相等,由
可得
故CD错误。
AB.当由A运动到时,以摆球为研究对象,受力分析如图甲所示
当由运动到时,受力分析如图乙所示
因此
故A错误,B正确。
故选B。
9.B
【解析】AC.两粒子进入磁场后均向下偏转,可知在A点均受到向下的洛伦兹力,由左手定则可知,两个粒子均带负电,AC错误;
BD.在磁场中由洛伦兹力提供向心力,则有
得
因两粒子进入磁场的速度相同,电荷量也相同,又在同一磁场中运动,故
B正确,D错误。
故选B。
10.D
【解析】如图所示
可求出从a点射出的粒子对应的圆心角为90°,从b点射出的粒子对应的圆心角为60°,由
式中为圆心角,可得
故D正确。
故选D。
11.A
【解析】如图所示,设圆弧的弦切角为α,弦长为l,由几何知识有
l=2rsinα
对导线分析受力,由平衡条件可得,导线所受安培力斜向右上方,则导线中的电流方向沿顺时针,且
2FTsinα=IlB
解得
对带电粒子,由洛伦兹力提供向心力有
解得
故A正确,BCD错误。
故选A。
12.(a)粒子受力方向为垂直速度向下;(b)粒子运动方向为垂直力的方向向左;(c)粒子运动方向为垂直力的方向向下;(d)粒子运动方向为垂直力的方向向右;(e)粒子受力方向为垂直纸面向外。
【解析】(a)粒子带负电,向右运动,根据左手定则判断粒子受力方向为垂直速度向下;
(b)粒子带负电,受力向上,根据左手定则,四指指向右,所以粒子运动方向为垂直力的方向向左;
(c)粒子带正电,受力向右,根据左手定则,四指指向下,所以粒子运动方向为垂直力的方向向下;
(d)粒子带正电,受力向下,根据左手定则,四指指向右,所以粒子运动方向为垂直力的方向向右;
(e)粒子带负电,向上运动,根据左手定则,大拇指指向外,所以粒子受力方向为垂直纸面向外。
13.(1) ;(2);(3)
【解析】(1)电子轨迹如图所示
(2)电子在上方磁场运动的周期
电子在下方磁场运动的周期
在一个周期内,电子在上方磁场运动轨迹为一个半圆,下方磁场运动轨迹为半圆,故电子运动一个周期的时间
(3)设电子在上方磁场做圆周运动的半径为R1,下方磁场做圆周运动的半径为R2,由牛顿第二定律
由几何关系知,电子运动一个周期沿x轴移动的距离
联立知
