华东师大版九年级上册 25.1.2. 用计算器做模拟试验课件(共21张PPT)
文档属性
| 名称 | 华东师大版九年级上册 25.1.2. 用计算器做模拟试验课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 351.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
25.1.2 用试验频率估计随机事件机会的大小
第25章 随机事件的概率
华东师大版 数学 九年级上册
1.理解试验次数较大时随机现象发生的频率趋于稳定这一规律.
2.学生懂得展开试验,通过试验数据的累加,分析,对比和讨论,探索频率与随机事件机会大小之间的关系.
一 预习目标
自主预习
1.在试验中体会:虽然每次的试验的结果_________,但是随着试验次数的______,随机现象发生的频率会________在某一个数值的附近.
2.可以用________估计随机事件在每一次试验时发生的机会的大小.
二 预习要点
无法预测
增加
稳定
频率
1.任意抛掷一枚均匀的硬币,会出现____种结果,这几种结果出现的可能性是________,都是______.
2.有大小两个正方体,每个正方体的六个面上分别标有数字1、2、3、4、5、6,将两个正方体投掷在桌面上,向上的一面数字之和为偶数的情形有________种,可能性是________;向上的一面数字之和为奇数的情形有________种,可能性是________.
三 预习自测
2
一样的
18
18
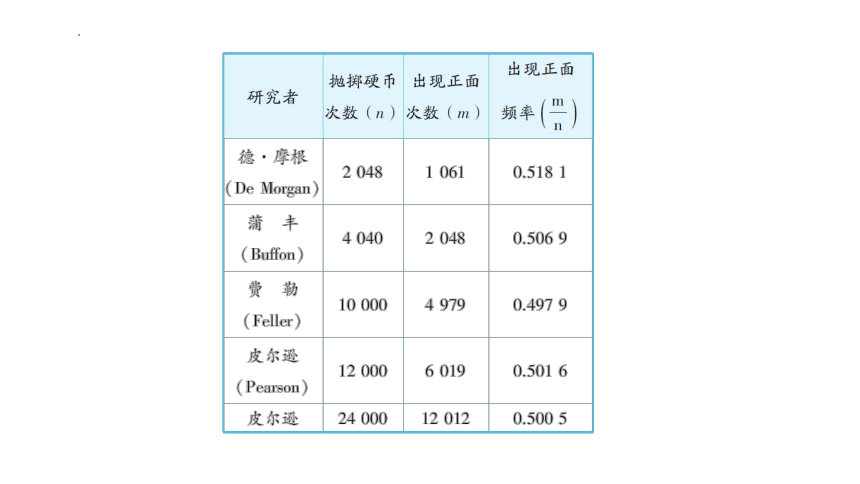
“抛硬币”游戏,在硬币未抛出之前,我们能否预测到每次抛出的结果?你的预测对吗?预测正确率有多少?其实历史上一些著名的科学家思考过这个问题.在重复试验中观察不确定现象,可以发现它们隐含的规律.下面记录了历史上抛硬币试验的若干结果.你发现了什么规律吗?
一 新知引入
互动课堂
二 合作探究
当试验次数不断增加时,“出现正面”的频率稳定在0.5左右.
自主学习教材P127-P131内容,小组讨论解决以下问题:
1.阅读新知引入,总结出抛硬币试验中,“出现正面”的频率有何规律.
2.与你的同学合作,做一做抛掷两枚硬币的试验,看看当抛掷次数很多以后,“出现两个正面”和“出现一正一反”这两个随机事件的频率是否也会变得稳定.并完成“出现两个正面”和“出现一正一反”的频率随抛掷次数变化趋势图.
略
3.抛掷两枚硬币的试验中,“出现两个正面”的频率逐渐稳定在__________左右;而“出现一正一反”的频率逐渐稳定在____________左右.
0.25
0.5
例1 从3名学生中,选出2人参加数学竞赛,其中任意一个人被选中的成功率为( )
三 新知应用
D
例2 有6张背面相同的扑克牌,正面上的数字分别是1,2,3,4,5,6.若将这6张牌背面朝上洗匀后,从中任意抽取一张,那么这张牌正面上的数字是奇数的机率为________.
例3 某水果公司以2元/千克的成本新进了10 000千克柑橘,公司希望这些柑橘能够获得5 000元利润.销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”统计,并把获得的数据记录在下表.
(1)请你帮忙完成此表:
柑橘总质量 (n)/千克 损坏的柑橘质量(m)/千克 柑橘损坏的频率( )
50 5.50 0.110
100 10.50 0.105
150 15.15
200 19.42
250 24.25
0.101
0.097
0.097
柑橘总质量 (n)/千克 损坏的柑橘质量(m)/千克 柑橘损坏的频率( )
300 30.93
350 35.32
400 39.24
450 44.57
500 51.54
0.103
0.101
0.098
0.099
0.103
(2)柑橘损坏的频率在左右摆动,并且随统计量的增加这种规律逐渐明显,所以估计柑橘的损坏率约为________,则柑橘完好率约为________.
0.1
0.9
(3)在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
(10 000×2+5 000)÷(10 000×0.9)≈2.8(元/千克)
答:每千克大约定价为2.8元比较合适.
1.抛掷两枚硬币的试验中,“出现两个正面”的频率逐渐稳定在 左右,下列说法正确的是( )
A.同时抛掷两枚硬币一次,一定不会“出现两个正面”
B.同时抛掷两枚硬币一次,一定会“出现两个正面”
C.同时抛掷两枚硬币4次,一定会“出现两个正面”
D.同时抛掷两枚硬币一次,则“出现两个正面”的可能性为25%
四 课堂小测
D
2.从生产的一批螺钉中抽取1 000个进行质量检查,结果发现有5个是次品,那么从中任取1个是次品的机率为( )
B
3.黑色、白色、黄色的筷子各有8根,混杂地放在一起,黑暗中想从这些筷子中取出颜色不同的两双筷子,问至少要取多少根才能保证达到要求?
解:8+2+1=11(根)
答:至少要取11根才能保证达到要求.
五 课堂小结
随着试验次数的增加,随机现象发生的频率会稳定在某一个数值的附近,因此用________估计随机事件在每一次试验时发生的机会的大小.
频率
再 见
25.1.2 用试验频率估计随机事件机会的大小
第25章 随机事件的概率
华东师大版 数学 九年级上册
1.理解试验次数较大时随机现象发生的频率趋于稳定这一规律.
2.学生懂得展开试验,通过试验数据的累加,分析,对比和讨论,探索频率与随机事件机会大小之间的关系.
一 预习目标
自主预习
1.在试验中体会:虽然每次的试验的结果_________,但是随着试验次数的______,随机现象发生的频率会________在某一个数值的附近.
2.可以用________估计随机事件在每一次试验时发生的机会的大小.
二 预习要点
无法预测
增加
稳定
频率
1.任意抛掷一枚均匀的硬币,会出现____种结果,这几种结果出现的可能性是________,都是______.
2.有大小两个正方体,每个正方体的六个面上分别标有数字1、2、3、4、5、6,将两个正方体投掷在桌面上,向上的一面数字之和为偶数的情形有________种,可能性是________;向上的一面数字之和为奇数的情形有________种,可能性是________.
三 预习自测
2
一样的
18
18
“抛硬币”游戏,在硬币未抛出之前,我们能否预测到每次抛出的结果?你的预测对吗?预测正确率有多少?其实历史上一些著名的科学家思考过这个问题.在重复试验中观察不确定现象,可以发现它们隐含的规律.下面记录了历史上抛硬币试验的若干结果.你发现了什么规律吗?
一 新知引入
互动课堂
二 合作探究
当试验次数不断增加时,“出现正面”的频率稳定在0.5左右.
自主学习教材P127-P131内容,小组讨论解决以下问题:
1.阅读新知引入,总结出抛硬币试验中,“出现正面”的频率有何规律.
2.与你的同学合作,做一做抛掷两枚硬币的试验,看看当抛掷次数很多以后,“出现两个正面”和“出现一正一反”这两个随机事件的频率是否也会变得稳定.并完成“出现两个正面”和“出现一正一反”的频率随抛掷次数变化趋势图.
略
3.抛掷两枚硬币的试验中,“出现两个正面”的频率逐渐稳定在__________左右;而“出现一正一反”的频率逐渐稳定在____________左右.
0.25
0.5
例1 从3名学生中,选出2人参加数学竞赛,其中任意一个人被选中的成功率为( )
三 新知应用
D
例2 有6张背面相同的扑克牌,正面上的数字分别是1,2,3,4,5,6.若将这6张牌背面朝上洗匀后,从中任意抽取一张,那么这张牌正面上的数字是奇数的机率为________.
例3 某水果公司以2元/千克的成本新进了10 000千克柑橘,公司希望这些柑橘能够获得5 000元利润.销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”统计,并把获得的数据记录在下表.
(1)请你帮忙完成此表:
柑橘总质量 (n)/千克 损坏的柑橘质量(m)/千克 柑橘损坏的频率( )
50 5.50 0.110
100 10.50 0.105
150 15.15
200 19.42
250 24.25
0.101
0.097
0.097
柑橘总质量 (n)/千克 损坏的柑橘质量(m)/千克 柑橘损坏的频率( )
300 30.93
350 35.32
400 39.24
450 44.57
500 51.54
0.103
0.101
0.098
0.099
0.103
(2)柑橘损坏的频率在左右摆动,并且随统计量的增加这种规律逐渐明显,所以估计柑橘的损坏率约为________,则柑橘完好率约为________.
0.1
0.9
(3)在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
(10 000×2+5 000)÷(10 000×0.9)≈2.8(元/千克)
答:每千克大约定价为2.8元比较合适.
1.抛掷两枚硬币的试验中,“出现两个正面”的频率逐渐稳定在 左右,下列说法正确的是( )
A.同时抛掷两枚硬币一次,一定不会“出现两个正面”
B.同时抛掷两枚硬币一次,一定会“出现两个正面”
C.同时抛掷两枚硬币4次,一定会“出现两个正面”
D.同时抛掷两枚硬币一次,则“出现两个正面”的可能性为25%
四 课堂小测
D
2.从生产的一批螺钉中抽取1 000个进行质量检查,结果发现有5个是次品,那么从中任取1个是次品的机率为( )
B
3.黑色、白色、黄色的筷子各有8根,混杂地放在一起,黑暗中想从这些筷子中取出颜色不同的两双筷子,问至少要取多少根才能保证达到要求?
解:8+2+1=11(根)
答:至少要取11根才能保证达到要求.
五 课堂小结
随着试验次数的增加,随机现象发生的频率会稳定在某一个数值的附近,因此用________估计随机事件在每一次试验时发生的机会的大小.
频率
再 见
