5.7三角函数的应用 同步练习(Word版含解析)
文档属性
| 名称 | 5.7三角函数的应用 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 00:00:00 | ||
图片预览



文档简介
人教A版(2019)必修第一册 5.7 三角函数的应用
一、单选题
1.把函数的图像向右平移个单位长度,再把所得图像上所有点的横坐标扩大到原来的2倍,纵坐标不变,得到函数的图像.则函数的一个解析式为( )
A. B. C. D.
2.为了得到函数的图象,可将的图象( )
A.向右平移个单位 B.向右平移个单位
C.向左平移个单位 D.向左平移个单位
3.某公园有一摩天轮,其直径为110米,逆时针匀速旋转一周所需时间约为28分钟,最高处距离地面120米,能够看到方圆40公里以内的景致.某乘客观光3分钟时看到一个与其视线水平的建筑物,试估计建筑物多高?( )
(参考数据:)
A.50 B.38 C.27 D.15
4.如图,某人在垂直于水平地面的墙面前的点处进行射击训练,已知点到墙面的距离为,某目标点沿墙面上的射线移动,此人为了准确瞄准目标点,需计算由点观察点的仰角的大小,若,则的最大值是( ).(仰角为直线与平面所成的角)
A. B. C. D.
5.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中使用.假设在水流量稳定的情况下,筒车的每一个盛水筒都做逆时针匀速圆周运动.现将筒车抽象为一个几何图形,如图所示,圆的半径为4米,盛水筒从点处开始运动,与水平面的所成角为,且2分钟恰好转动1圈,则盛水筒距离水面的高度(单位:米)与时间(单位:秒)之间的函数关系式是( )
A. B.
C. D.
6.如图,A是轮子外边沿上的一点,轮子半径为.若轮子从图中位置向右无滑动滚动,则当滚动的水平距离为时,下列描述正确的是( )(参考数据:)
A.点A在轮子的左下位置,距离地面约为
B.点A在轮子的右下位置,距离地面约为
C.点A在轮子的左下位置,距离地面约为
D.点A在轮子的右下位置,距离地面约为
7.若,则( )
A. B. C. D.
8.心脏每跳动一次,就完成一次收缩和舒张.心脏跳动时,血压在增大或缩小,并呈周期性变化,血压的最大值和最小值分别称为收缩压和舒张压.某人的血压满足函数,其中为血压(单位:),t为时间(单位:),则相邻的收缩压和舒张压的时间间隔是( )
A. B. C. D.
9.动点在圆上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周,已知时间时,点的坐标是,则当时,动点的纵坐标关于(单位:秒)的函数的单调递增区间是
A. B. C. D.和
10.如图,某港口一天6时到18时的水深变化曲线近似满足函数关系式y=3sin+k,据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6 C.8 D.10
11.某艺术展览馆在开馆时间段(9:00—16:00)的参观人数(单位:千)随时间(单位:时)的变化近似满足函数关系,且下午两点整参观人数为7千,则开馆中参观人数的最大值为( )
A.1万 B.9千 C.8千 D.7千
12.函数的图象与直线有且仅有两个不同的交点,则k的取值范围是( )
A. B. C. D.
二、填空题
13.下表中给出了在24小时内人的体温的变化(从夜间零点开始计时).
时间(x) 0 2 4 6 8 10 12
温度(y) 36.8 36.7 36.6 36.7 36.8 37.0 37.2
时间(x) 14 16 18 20 22 24
温度(y) 37.3 37.4 37.3 37.2 37.0 36.8
选用一个三角函数模型来近似地描述这些数据,则该模型为_________
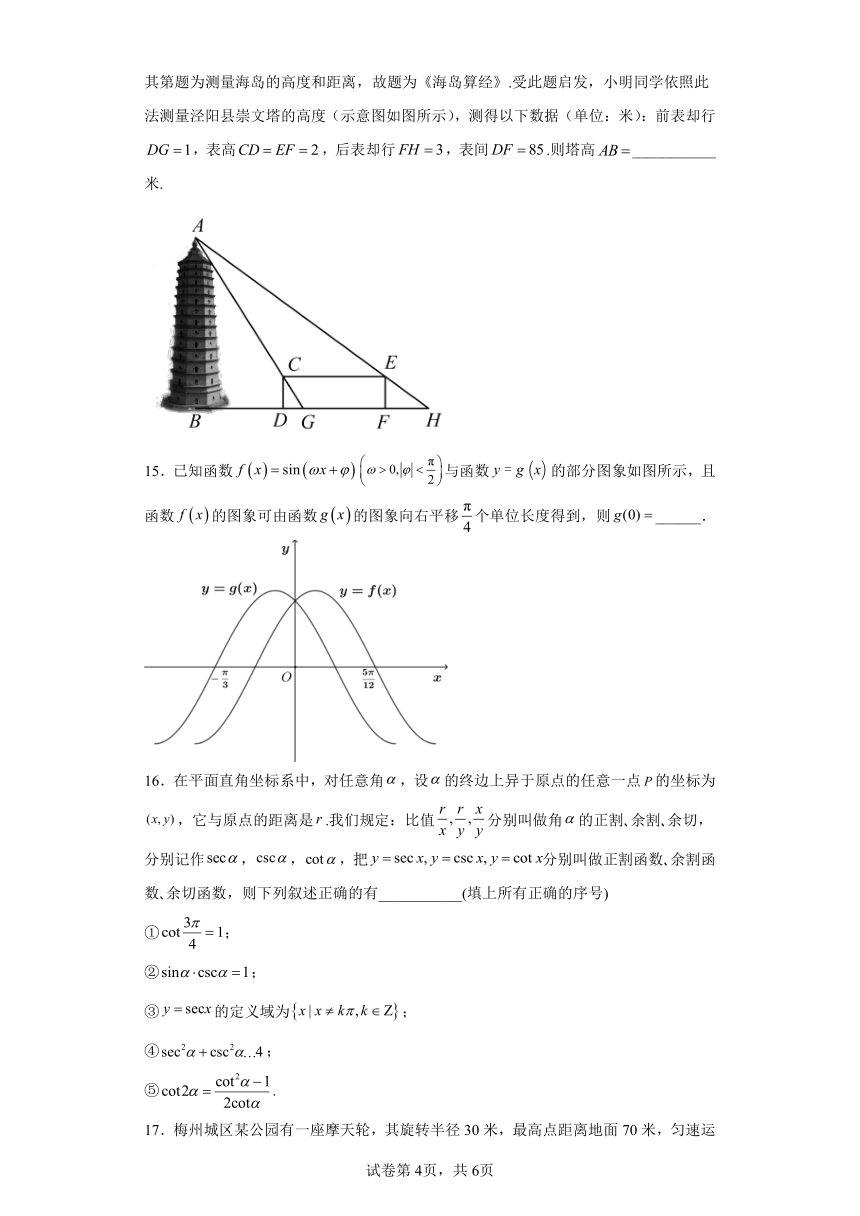
14.魏晋南北朝(公元220-581)时期,中国数学在测量学取得了长足进展.刘徽提出重差术,应用中国传统的出入相补原理,通过多次观测测量山高水深等数值,进而使中国的测量学达到登峰造极的地步,超越西方约一千年,关于重差术的注文在唐代成书,因其第题为测量海岛的高度和距离,故题为《海岛算经》.受此题启发,小明同学依照此法测量泾阳县崇文塔的高度(示意图如图所示),测得以下数据(单位:米):前表却行,表高,后表却行,表间.则塔高___________米.
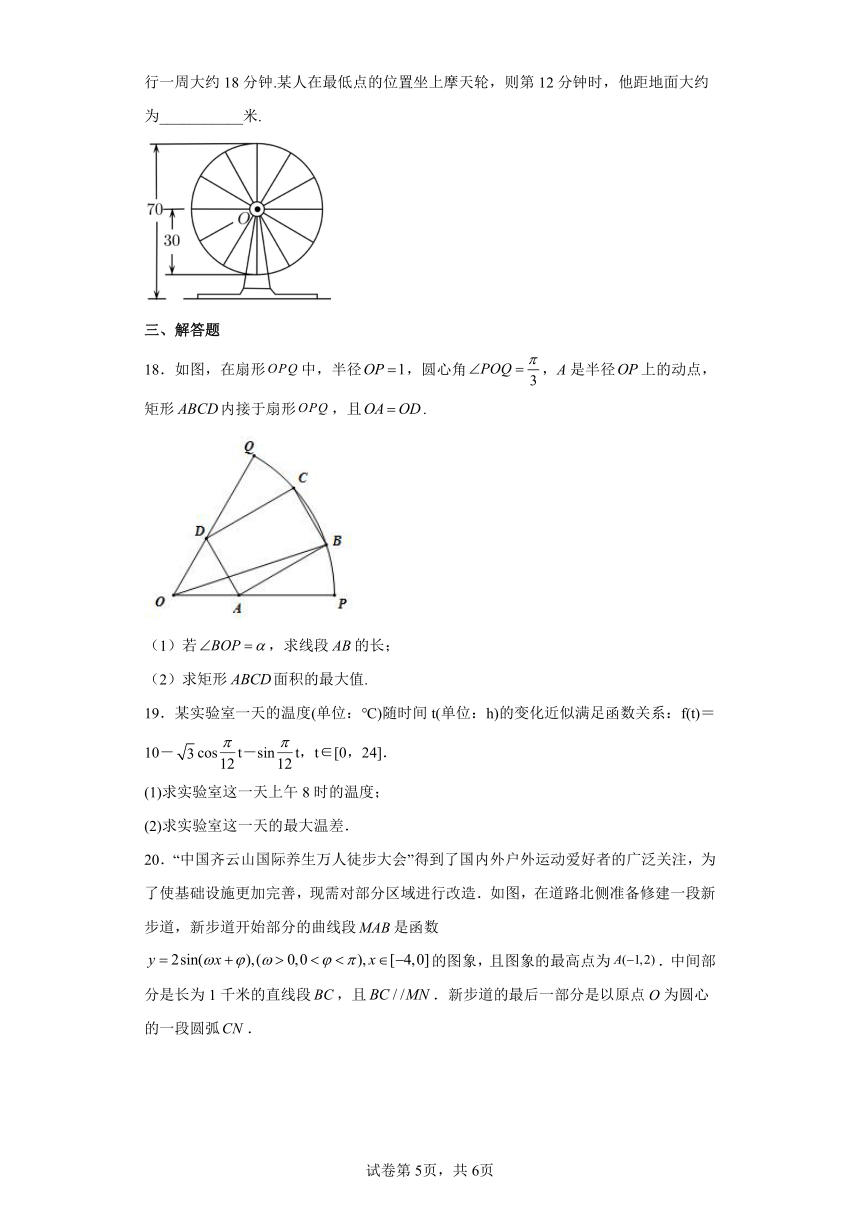
15.已知函数与函数的部分图象如图所示,且函数的图象可由函数的图象向右平移个单位长度得到,则______.
16.在平面直角坐标系中,对任意角,设的终边上异于原点的任意一点的坐标为,它与原点的距离是.我们规定:比值分别叫做角的正割 余割 余切,分别记作,,,把分别叫做正割函数 余割函数 余切函数,则下列叙述正确的有___________(填上所有正确的序号)
①;
②;
③的定义域为;
④;
⑤.
17.梅州城区某公园有一座摩天轮,其旋转半径30米,最高点距离地面70米,匀速运行一周大约18分钟.某人在最低点的位置坐上摩天轮,则第12分钟时,他距地面大约为___________米.
三、解答题
18.如图,在扇形中,半径,圆心角,A是半径上的动点,矩形内接于扇形,且.
(1)若,求线段的长;
(2)求矩形面积的最大值.
19.某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:f(t)=10-cost-sint,t∈[0,24].
(1)求实验室这一天上午8时的温度;
(2)求实验室这一天的最大温差.
20.“中国齐云山国际养生万人徒步大会”得到了国内外户外运动爱好者的广泛关注,为了使基础设施更加完善,现需对部分区域进行改造.如图,在道路北侧准备修建一段新步道,新步道开始部分的曲线段是函数的图象,且图象的最高点为.中间部分是长为1千米的直线段,且.新步道的最后一部分是以原点O为圆心的一段圆弧.
(1)试确定的值;
(2)若计划在扇形区域内划出面积尽可能大的矩形区域建服务站,并要求矩形一边紧靠道路,顶点Q落在半径上,另一顶点P落在圆弧上.记,请问矩形面积最大时应取何值,并求出最大面积?
21.筒车是我国古代发明的一种水利灌溉工且,因其经济又环保,至今还在农业生产中使用,明朝科学家徐光启所著《农政全书》中描绘了简车的工作原理.如图,一个半径为3m的筒车,按逆时针方向转一周的时长为2min,筒车的轴心O距离水面的高度为1.5m.简车上均匀分布了12个盛水筒,设筒车上的某个盛水筒Р到水面的距离为y(单位:m)(在水面下则y为负数),若以盛水筒P刚浮出水面时开始计算时间,则y与时间t(单位:min)之间的关系为.
(1)求,,,的值;
(2)盛水筒出水后至少经过多少时间就可以到达最高点;
(3)在筒车运行的过程中,求相邻两个盛水筒距离地面的高度差h(单位:m)关于t的函数解析式,并求出高度差的最大值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
将函数的图像所有点的横坐标缩短到原来的,纵坐标不变,再向左平移个单位长度即得解.
【详解】
解:将函数的图像所有点的横坐标缩短到原来的,纵坐标不变,得到,再把函数的图象向左平移个单位长度,得到.
故选:B
2.A
将函数化为,根据图象平移变换可得结果.
【详解】
由题意得:
向右平移个单位即可得到的图象
故选:A.
该题考查的是三角函数的平移变换问题,关键是能够理解平移的量是自变量本身的变化量,属于基础题目.
3.C
作出简图,求出3分钟走过的角度,从而求出三分钟后距摩天轮最低点的高度,进而求出建筑物的高度.
【详解】
设走了3分钟到达(如图所示),
走过的圆心角为,
,
因为 ,
所以,
所以
所以,
所以建筑物的高度:
故选:C
4.D
由题可得,,过作,交于,连接,则,设,分类讨论,若在线段上,则,可求出和,从而可得出,利用函数的单调性,可得出时,取得最大值;若在的延长线上,同理求出和,可得出,可得当时,函数取得最大值;结合两种情况的结果,即可得出结论.
【详解】
解:,,
由勾股定理知,,
过点作交于,连结,则,
设,
若在线段上,则,
由,得,
在直角中,,
,
令,则函数在,单调递减,
时,取得最大值为;
若在的延长线上,,
在直角中,,
,
令,则可得时,函数取得最大值.
故答案为:.
5.A
有题意设,根据最高、最低高度,周期和初始高度,可得结果.
【详解】
设距离水面的高度H与时间t的函数关系式为,
周期为120s,,
最高点的纵坐标为,
最低点的纵坐标为,
所以,
当t=0时,H=0,,
所以.
故选:A.
6.A
计算出车轮转动的周期数即可得结果.
【详解】
车轮的周长为,
当滚动的水平距离为时,即车轮转动个周期,
即点A在轮子的左下位置,距离地面约为,
故选:A.
7.A
利用两角和与差的三角的正弦,将,转化为,其中,,则有,然后求解、,求出的值,利用二倍角的正切公式可求得的值.
【详解】
因为,所以,
即,,即,其中,,
,,,,
,,
,.
故选:A.
本题主要考查两角和与差的三角函数的正用和逆用,还考查了转化化归的思想和运算求解的能力,属于中档题.
8.A
相邻血压的最大值与最小值之间的间隔,由三角函数性质易知为半个周期,求得血压函数的周期即可求得.
【详解】
由题知,血压的最大值与最小值分别为收缩压和舒张压,
又血压函数为正弦三角函数,则相邻的收缩压和舒张压即血压函数的半个周期,
则,时间间隔为.
故选:A.
9.D
【详解】
试题分析:时,点的坐标是,所以点的初始角为,当点转过的角度在或时,动点的纵坐标关于(单位:秒)的函数的单调递增,因为12秒旋转一周,所以每秒转过的角度是,,则当时,动点的纵坐标关于(单位:秒)的函数的单调递增区间是和,故选D.
考点:1、三角的定义;2、三角函数的图象与性质.
【方法点睛】三角函数的定义是研究三角问题的基础,在数学学习中,利用定义解题是一种良好的思维方式,因为定义是一切基本问题的出发点,对数学定义的反复应用必将增强对知识的理解与掌握,是学好数学的有效途径.
10.C
由图中最小值求出,从而可得最大值.
【详解】
由题干图易得ymin=k-3=2,则k=5.
∴ymax=k+3=8.
故选:C
本题考查()的性质,的最大值为,最小值为.
11.B
利用当时,,求出,由,利用正弦函数的性质即可求解.
【详解】
下午两点整即,当时,.
即,∴,
∵当时,,
∴当时,取得最大值,且最大值为.
故选:B
本题考查了三角函数的性质求解析式、三角函数的应用,考查了基本运算求解能力,属于基础题.
12.B
结合题意化简函数的解析式,然后根据解析式作出函数的图象,进而数形结合即可求出结果.
【详解】
因为时,,则,
因为时,,则,
故,
作出函数图象:
数形结合即可得到,
故选:B.
13.,
设时的体温为,然后求出,,,的值即可;
【详解】
解:设时的体温为,则,,
,由,即,即,解得,不妨取,
故可用,来近似地描述这些数据;
故答案为:,
14.87
可看出,,从而可得出,这样即可求出的值.
【详解】
解:根据题意,,,
,解得(米,
(米.
故答案为:87
15.
求出点向右平移个单位长度可得,结合函数图象可得
,解方程组可求出的值,结合平移求出的解析式,进而求出.
【详解】
由题意可知将函数图象上的点向右平移个单位长度,
可得的图象与轴负半轴的第一个交点,坐标为,
因为的图象与轴正半轴的第一个交点为,
所以,解得,所以,
,故.
故答案为:.
16.②④⑤
由题设新定义知:,,,由、、、以及正切二倍角公式,即可判断各项的正误.
【详解】
①,故错误;
②,故正确;
③,即,有,故错误;
④,故正确;
⑤,所以,故正确.
故答案为:②④⑤
关键点点睛:新定义有,,,结合三角恒等变换判断各项的正误.
17.55
建立平面直角坐标系,第分钟时所在位置的高度为,设出其三角函数的表达式,由题意,得出其周期,求出解析式,然后将代入,可得答案.
【详解】
如图设为地面,圆为摩天轮,其旋转半径30米,最高点距离地面70米.
则摩天轮的最低点离地面10米,即
以所在直线为轴,所在直线为轴,建立平面直角坐标系.
某人在最低点的位置坐上摩天轮,则第分钟时所在位置的高度为
则
由题意,,则,所以
当时,
故答案为:55
18.(1);(2)矩形面积的最大值为.
(1)由题意可得,过作的垂线,垂足为,在中,即可求解.
(2)由(1)可得,,从而可得,,根据矩形面积公式以及辅助角公式即可求解.
【详解】
(1)且,
为等边三角形,,
又四边形为矩形,,,
在扇形中,半径,
过作的垂线,垂足为,
,
在中,.
(2)矩形面积,
设,由(1)可知,,
,,
,
,
,,
当,即时,矩形面积的最大值,
最大值为.
19.(1)10 ℃(2)4 ℃
(1)即求f(8);
(2)利用辅助角公式把f(t)化成的形式,求出f(t)的最大值和最小值,从而可求最大温差.
【详解】
解:(1)f(8)=10-cos-sin=10-cos-sin=10-×-=10.
故实验室上午8时的温度为10 ℃.
(2)因为f(t)=10-2=10-2sin,又0≤t<24,所以≤t+<,-1≤sin≤1.
当t=2时,sin=1;当t=14时,sin=-1.
于是f(t)在[0,24)上取得最大值12,取得最小值8.
故实验室这一天最高温度为12 ℃,最低温度为8 ℃,最大温差为4 ℃.
本题主要考查利用三角函数辅助角公式将原函数进行化简,再运用三角函数的性质求解.
20.(1),;(2)当时,面积最大为.
(1)先根据周期计算出的值,然后利用图象过点求解出的值;
(2)先求解出点坐标并计算出长度,然后设出点坐标并表示出的大小,根据矩形面积公式结合三角恒等变换的化简以及正弦函数的性质求解出最大面积以及对应的值.
【详解】
(1)∵,∴,∴.
图象过,∴,又,∴.
(2)由(1)知,交y轴于,又,
∴.
又,∴,,
∴
又,∴时,此时矩形面积最大为.
21.(1),,;(2);(3)h,,最大值为.
(1)直接由题意求出,,,的值;
(2)求出函数解析式,由函数最大值为,可得,即,取得答案;
(3)设两个相邻的盛水筒分别用和表示(不妨设领先于,则,分别求出经过相邻两个盛水筒距离水面的高度,作差后利用三角函数求最值.
【详解】
解:(1)由题知,得,
由题意得,,.
(2)由,得,
所以,即,
当时,盛水筒出水后第一次到达最高点,此时.
(3)设两个相邻的盛水筒分别用A和B表示(A领先于B),则经过相邻两个盛水筒距离水面的高度分别和,
所以,,
所以的最大值为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.把函数的图像向右平移个单位长度,再把所得图像上所有点的横坐标扩大到原来的2倍,纵坐标不变,得到函数的图像.则函数的一个解析式为( )
A. B. C. D.
2.为了得到函数的图象,可将的图象( )
A.向右平移个单位 B.向右平移个单位
C.向左平移个单位 D.向左平移个单位
3.某公园有一摩天轮,其直径为110米,逆时针匀速旋转一周所需时间约为28分钟,最高处距离地面120米,能够看到方圆40公里以内的景致.某乘客观光3分钟时看到一个与其视线水平的建筑物,试估计建筑物多高?( )
(参考数据:)
A.50 B.38 C.27 D.15
4.如图,某人在垂直于水平地面的墙面前的点处进行射击训练,已知点到墙面的距离为,某目标点沿墙面上的射线移动,此人为了准确瞄准目标点,需计算由点观察点的仰角的大小,若,则的最大值是( ).(仰角为直线与平面所成的角)
A. B. C. D.
5.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中使用.假设在水流量稳定的情况下,筒车的每一个盛水筒都做逆时针匀速圆周运动.现将筒车抽象为一个几何图形,如图所示,圆的半径为4米,盛水筒从点处开始运动,与水平面的所成角为,且2分钟恰好转动1圈,则盛水筒距离水面的高度(单位:米)与时间(单位:秒)之间的函数关系式是( )
A. B.
C. D.
6.如图,A是轮子外边沿上的一点,轮子半径为.若轮子从图中位置向右无滑动滚动,则当滚动的水平距离为时,下列描述正确的是( )(参考数据:)
A.点A在轮子的左下位置,距离地面约为
B.点A在轮子的右下位置,距离地面约为
C.点A在轮子的左下位置,距离地面约为
D.点A在轮子的右下位置,距离地面约为
7.若,则( )
A. B. C. D.
8.心脏每跳动一次,就完成一次收缩和舒张.心脏跳动时,血压在增大或缩小,并呈周期性变化,血压的最大值和最小值分别称为收缩压和舒张压.某人的血压满足函数,其中为血压(单位:),t为时间(单位:),则相邻的收缩压和舒张压的时间间隔是( )
A. B. C. D.
9.动点在圆上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周,已知时间时,点的坐标是,则当时,动点的纵坐标关于(单位:秒)的函数的单调递增区间是
A. B. C. D.和
10.如图,某港口一天6时到18时的水深变化曲线近似满足函数关系式y=3sin+k,据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6 C.8 D.10
11.某艺术展览馆在开馆时间段(9:00—16:00)的参观人数(单位:千)随时间(单位:时)的变化近似满足函数关系,且下午两点整参观人数为7千,则开馆中参观人数的最大值为( )
A.1万 B.9千 C.8千 D.7千
12.函数的图象与直线有且仅有两个不同的交点,则k的取值范围是( )
A. B. C. D.
二、填空题
13.下表中给出了在24小时内人的体温的变化(从夜间零点开始计时).
时间(x) 0 2 4 6 8 10 12
温度(y) 36.8 36.7 36.6 36.7 36.8 37.0 37.2
时间(x) 14 16 18 20 22 24
温度(y) 37.3 37.4 37.3 37.2 37.0 36.8
选用一个三角函数模型来近似地描述这些数据,则该模型为_________
14.魏晋南北朝(公元220-581)时期,中国数学在测量学取得了长足进展.刘徽提出重差术,应用中国传统的出入相补原理,通过多次观测测量山高水深等数值,进而使中国的测量学达到登峰造极的地步,超越西方约一千年,关于重差术的注文在唐代成书,因其第题为测量海岛的高度和距离,故题为《海岛算经》.受此题启发,小明同学依照此法测量泾阳县崇文塔的高度(示意图如图所示),测得以下数据(单位:米):前表却行,表高,后表却行,表间.则塔高___________米.
15.已知函数与函数的部分图象如图所示,且函数的图象可由函数的图象向右平移个单位长度得到,则______.
16.在平面直角坐标系中,对任意角,设的终边上异于原点的任意一点的坐标为,它与原点的距离是.我们规定:比值分别叫做角的正割 余割 余切,分别记作,,,把分别叫做正割函数 余割函数 余切函数,则下列叙述正确的有___________(填上所有正确的序号)
①;
②;
③的定义域为;
④;
⑤.
17.梅州城区某公园有一座摩天轮,其旋转半径30米,最高点距离地面70米,匀速运行一周大约18分钟.某人在最低点的位置坐上摩天轮,则第12分钟时,他距地面大约为___________米.
三、解答题
18.如图,在扇形中,半径,圆心角,A是半径上的动点,矩形内接于扇形,且.
(1)若,求线段的长;
(2)求矩形面积的最大值.
19.某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:f(t)=10-cost-sint,t∈[0,24].
(1)求实验室这一天上午8时的温度;
(2)求实验室这一天的最大温差.
20.“中国齐云山国际养生万人徒步大会”得到了国内外户外运动爱好者的广泛关注,为了使基础设施更加完善,现需对部分区域进行改造.如图,在道路北侧准备修建一段新步道,新步道开始部分的曲线段是函数的图象,且图象的最高点为.中间部分是长为1千米的直线段,且.新步道的最后一部分是以原点O为圆心的一段圆弧.
(1)试确定的值;
(2)若计划在扇形区域内划出面积尽可能大的矩形区域建服务站,并要求矩形一边紧靠道路,顶点Q落在半径上,另一顶点P落在圆弧上.记,请问矩形面积最大时应取何值,并求出最大面积?
21.筒车是我国古代发明的一种水利灌溉工且,因其经济又环保,至今还在农业生产中使用,明朝科学家徐光启所著《农政全书》中描绘了简车的工作原理.如图,一个半径为3m的筒车,按逆时针方向转一周的时长为2min,筒车的轴心O距离水面的高度为1.5m.简车上均匀分布了12个盛水筒,设筒车上的某个盛水筒Р到水面的距离为y(单位:m)(在水面下则y为负数),若以盛水筒P刚浮出水面时开始计算时间,则y与时间t(单位:min)之间的关系为.
(1)求,,,的值;
(2)盛水筒出水后至少经过多少时间就可以到达最高点;
(3)在筒车运行的过程中,求相邻两个盛水筒距离地面的高度差h(单位:m)关于t的函数解析式,并求出高度差的最大值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
将函数的图像所有点的横坐标缩短到原来的,纵坐标不变,再向左平移个单位长度即得解.
【详解】
解:将函数的图像所有点的横坐标缩短到原来的,纵坐标不变,得到,再把函数的图象向左平移个单位长度,得到.
故选:B
2.A
将函数化为,根据图象平移变换可得结果.
【详解】
由题意得:
向右平移个单位即可得到的图象
故选:A.
该题考查的是三角函数的平移变换问题,关键是能够理解平移的量是自变量本身的变化量,属于基础题目.
3.C
作出简图,求出3分钟走过的角度,从而求出三分钟后距摩天轮最低点的高度,进而求出建筑物的高度.
【详解】
设走了3分钟到达(如图所示),
走过的圆心角为,
,
因为 ,
所以,
所以
所以,
所以建筑物的高度:
故选:C
4.D
由题可得,,过作,交于,连接,则,设,分类讨论,若在线段上,则,可求出和,从而可得出,利用函数的单调性,可得出时,取得最大值;若在的延长线上,同理求出和,可得出,可得当时,函数取得最大值;结合两种情况的结果,即可得出结论.
【详解】
解:,,
由勾股定理知,,
过点作交于,连结,则,
设,
若在线段上,则,
由,得,
在直角中,,
,
令,则函数在,单调递减,
时,取得最大值为;
若在的延长线上,,
在直角中,,
,
令,则可得时,函数取得最大值.
故答案为:.
5.A
有题意设,根据最高、最低高度,周期和初始高度,可得结果.
【详解】
设距离水面的高度H与时间t的函数关系式为,
周期为120s,,
最高点的纵坐标为,
最低点的纵坐标为,
所以,
当t=0时,H=0,,
所以.
故选:A.
6.A
计算出车轮转动的周期数即可得结果.
【详解】
车轮的周长为,
当滚动的水平距离为时,即车轮转动个周期,
即点A在轮子的左下位置,距离地面约为,
故选:A.
7.A
利用两角和与差的三角的正弦,将,转化为,其中,,则有,然后求解、,求出的值,利用二倍角的正切公式可求得的值.
【详解】
因为,所以,
即,,即,其中,,
,,,,
,,
,.
故选:A.
本题主要考查两角和与差的三角函数的正用和逆用,还考查了转化化归的思想和运算求解的能力,属于中档题.
8.A
相邻血压的最大值与最小值之间的间隔,由三角函数性质易知为半个周期,求得血压函数的周期即可求得.
【详解】
由题知,血压的最大值与最小值分别为收缩压和舒张压,
又血压函数为正弦三角函数,则相邻的收缩压和舒张压即血压函数的半个周期,
则,时间间隔为.
故选:A.
9.D
【详解】
试题分析:时,点的坐标是,所以点的初始角为,当点转过的角度在或时,动点的纵坐标关于(单位:秒)的函数的单调递增,因为12秒旋转一周,所以每秒转过的角度是,,则当时,动点的纵坐标关于(单位:秒)的函数的单调递增区间是和,故选D.
考点:1、三角的定义;2、三角函数的图象与性质.
【方法点睛】三角函数的定义是研究三角问题的基础,在数学学习中,利用定义解题是一种良好的思维方式,因为定义是一切基本问题的出发点,对数学定义的反复应用必将增强对知识的理解与掌握,是学好数学的有效途径.
10.C
由图中最小值求出,从而可得最大值.
【详解】
由题干图易得ymin=k-3=2,则k=5.
∴ymax=k+3=8.
故选:C
本题考查()的性质,的最大值为,最小值为.
11.B
利用当时,,求出,由,利用正弦函数的性质即可求解.
【详解】
下午两点整即,当时,.
即,∴,
∵当时,,
∴当时,取得最大值,且最大值为.
故选:B
本题考查了三角函数的性质求解析式、三角函数的应用,考查了基本运算求解能力,属于基础题.
12.B
结合题意化简函数的解析式,然后根据解析式作出函数的图象,进而数形结合即可求出结果.
【详解】
因为时,,则,
因为时,,则,
故,
作出函数图象:
数形结合即可得到,
故选:B.
13.,
设时的体温为,然后求出,,,的值即可;
【详解】
解:设时的体温为,则,,
,由,即,即,解得,不妨取,
故可用,来近似地描述这些数据;
故答案为:,
14.87
可看出,,从而可得出,这样即可求出的值.
【详解】
解:根据题意,,,
,解得(米,
(米.
故答案为:87
15.
求出点向右平移个单位长度可得,结合函数图象可得
,解方程组可求出的值,结合平移求出的解析式,进而求出.
【详解】
由题意可知将函数图象上的点向右平移个单位长度,
可得的图象与轴负半轴的第一个交点,坐标为,
因为的图象与轴正半轴的第一个交点为,
所以,解得,所以,
,故.
故答案为:.
16.②④⑤
由题设新定义知:,,,由、、、以及正切二倍角公式,即可判断各项的正误.
【详解】
①,故错误;
②,故正确;
③,即,有,故错误;
④,故正确;
⑤,所以,故正确.
故答案为:②④⑤
关键点点睛:新定义有,,,结合三角恒等变换判断各项的正误.
17.55
建立平面直角坐标系,第分钟时所在位置的高度为,设出其三角函数的表达式,由题意,得出其周期,求出解析式,然后将代入,可得答案.
【详解】
如图设为地面,圆为摩天轮,其旋转半径30米,最高点距离地面70米.
则摩天轮的最低点离地面10米,即
以所在直线为轴,所在直线为轴,建立平面直角坐标系.
某人在最低点的位置坐上摩天轮,则第分钟时所在位置的高度为
则
由题意,,则,所以
当时,
故答案为:55
18.(1);(2)矩形面积的最大值为.
(1)由题意可得,过作的垂线,垂足为,在中,即可求解.
(2)由(1)可得,,从而可得,,根据矩形面积公式以及辅助角公式即可求解.
【详解】
(1)且,
为等边三角形,,
又四边形为矩形,,,
在扇形中,半径,
过作的垂线,垂足为,
,
在中,.
(2)矩形面积,
设,由(1)可知,,
,,
,
,
,,
当,即时,矩形面积的最大值,
最大值为.
19.(1)10 ℃(2)4 ℃
(1)即求f(8);
(2)利用辅助角公式把f(t)化成的形式,求出f(t)的最大值和最小值,从而可求最大温差.
【详解】
解:(1)f(8)=10-cos-sin=10-cos-sin=10-×-=10.
故实验室上午8时的温度为10 ℃.
(2)因为f(t)=10-2=10-2sin,又0≤t<24,所以≤t+<,-1≤sin≤1.
当t=2时,sin=1;当t=14时,sin=-1.
于是f(t)在[0,24)上取得最大值12,取得最小值8.
故实验室这一天最高温度为12 ℃,最低温度为8 ℃,最大温差为4 ℃.
本题主要考查利用三角函数辅助角公式将原函数进行化简,再运用三角函数的性质求解.
20.(1),;(2)当时,面积最大为.
(1)先根据周期计算出的值,然后利用图象过点求解出的值;
(2)先求解出点坐标并计算出长度,然后设出点坐标并表示出的大小,根据矩形面积公式结合三角恒等变换的化简以及正弦函数的性质求解出最大面积以及对应的值.
【详解】
(1)∵,∴,∴.
图象过,∴,又,∴.
(2)由(1)知,交y轴于,又,
∴.
又,∴,,
∴
又,∴时,此时矩形面积最大为.
21.(1),,;(2);(3)h,,最大值为.
(1)直接由题意求出,,,的值;
(2)求出函数解析式,由函数最大值为,可得,即,取得答案;
(3)设两个相邻的盛水筒分别用和表示(不妨设领先于,则,分别求出经过相邻两个盛水筒距离水面的高度,作差后利用三角函数求最值.
【详解】
解:(1)由题知,得,
由题意得,,.
(2)由,得,
所以,即,
当时,盛水筒出水后第一次到达最高点,此时.
(3)设两个相邻的盛水筒分别用A和B表示(A领先于B),则经过相邻两个盛水筒距离水面的高度分别和,
所以,,
所以的最大值为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
