6.1分类加法计数原理与分步乘法计数原理 同步练习(Word版含解析)
文档属性
| 名称 | 6.1分类加法计数原理与分步乘法计数原理 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 394.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 00:00:00 | ||
图片预览




文档简介
人教A版(2019)选择性必修第三册 6.1分类加法计数原理与分步乘法计数原理
一、单选题
1.某省专家组为评审某市是否达到“生态园林城市”的标准,从包含甲、乙两位专家在内的8人中选出4人组成评审委员会,若甲、乙两位专家已经被邀请,则组成该评审委员会的不同方式共有( )
A.30种 B.15种 C.20种 D.25种
2.从3名女同学和2名男同学中选1人主持主题班会,则不同的选法种数为( )
A.6 B.5 C.3 D.2
3.为响应国家“节约粮食”的号召,某同学决定在某食堂提供的2种主食、3种素菜、2种大荤、4种小荤中选取一种主食、一种素菜、一种荤菜作为今日伙食,并在用餐时积极践行“光盘行动”,则不同的选取方法有( )
A.48种 B.36种 C.24种 D.12种
4.用红,黄,蓝,绿,黑这5种颜色随机给如图所示的四块三角形区域涂色,则“在任意两个有公共边的三角形所涂颜色不同”的概率为( )
A. B. C. D.
5.今年我国中医药选出的“三药三方”对治疗新冠肺炎均有显著效果,功不可没.“三药”分别为金花清感颗粒、连花清瘟胶囊、血必清注射液;“三方”分别为清肺排毒汤、化湿败毒方、宜肺败毒方,若某医生从“三药三方”中随机选出2种,则恰好选出1药1方的方法种数为( )
A.15 B.30 C.6 D.9
6.7个人排成一排准备照一张合影,其中甲、乙要求相邻,丙、丁要求分开,则不同的排法有( )
A.480种 B.720种 C.960种 D.1200种
7.、、、、五人排一个5天的值日表,每天由一人值日,每人可以值多天或不值,但相邻的两天不能由同一人值,那么值日表的排法种数为( )
A.120 B.324 C.720 D.1280
8.4名学生报名参加语、数、英兴趣小组,每人选报1种,则不同方法有( )
A.种 B.种 C.种 D.种
9.算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如图:
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图;
如果把5根算筹以适当的方式全部放入下面的表格中,那么可以表示的三位数的个数为( )
A.46 B.44 C.42 D.40
10.把5名同学分配到图书馆、食堂、学生活动中心做志愿者,每个地方至少去一个同学,不同的安排方法共有( )种.
A.60 B.72 C.96 D.150
11.设,与是的子集,若,则称为一个“理想配集”.那么符合此条件的“理想配集”(规定与是两个不同的“理想配集”)的个数是( )
A.16 B.9 C.8 D.4
12.中园古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”主要指德育;“乐”主要指美育;“射”和“御”就是体育和劳动;“书”指各种历史文化知识;“数”指数学.某校国学社团开展“六艺”讲座活动,每周安排一次讲座,共讲六次.讲座次序要求“射”不在第一次,“数”和“乐”两次不相邻,则“六艺”讲座不同的次序共有( )
A.408种 B.240种 C.1092种. D.120种
二、填空题
13.某学校有东、南、西、北四个校门.受新冠肺炎疫情的影响,学校对进入四个校门做出如下规定:学生只能从东门或西门进入校园,教师只能从南门或北门进入校园.现有3名教师和4名学生要进入校园(不分先后顺序),请问进入校园的方式共有_________种.(用数字作答)
14.若三角形的三边长均为正整数,其中一边长为3,另外两边长分别为,,且满足,则这样的三角形有______个.
15.甲、乙、丙3个班各有3,5,2名三好学生,现准备推选2名来自不同班的三好学生去参加校三好学生代表大会,共有______种推选方法.
16.如图,用四种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法的种数为______(用数字作答)
17.某班一天上午有4节课,每节都需要安排一名教师去上课,现从,,,,,6名教师中安排4人分别上一节课,第一节课只能从,两人中安排一人,第四节课只能从,两人中安排一人,则不同的安排方案共有______种.(用数字作答)
三、解答题
18.从1~20中任选一个质数作为被减数,再从1~10中任选一个数作为减数,写成一个减法算式,共可得到多少个不同的算式?
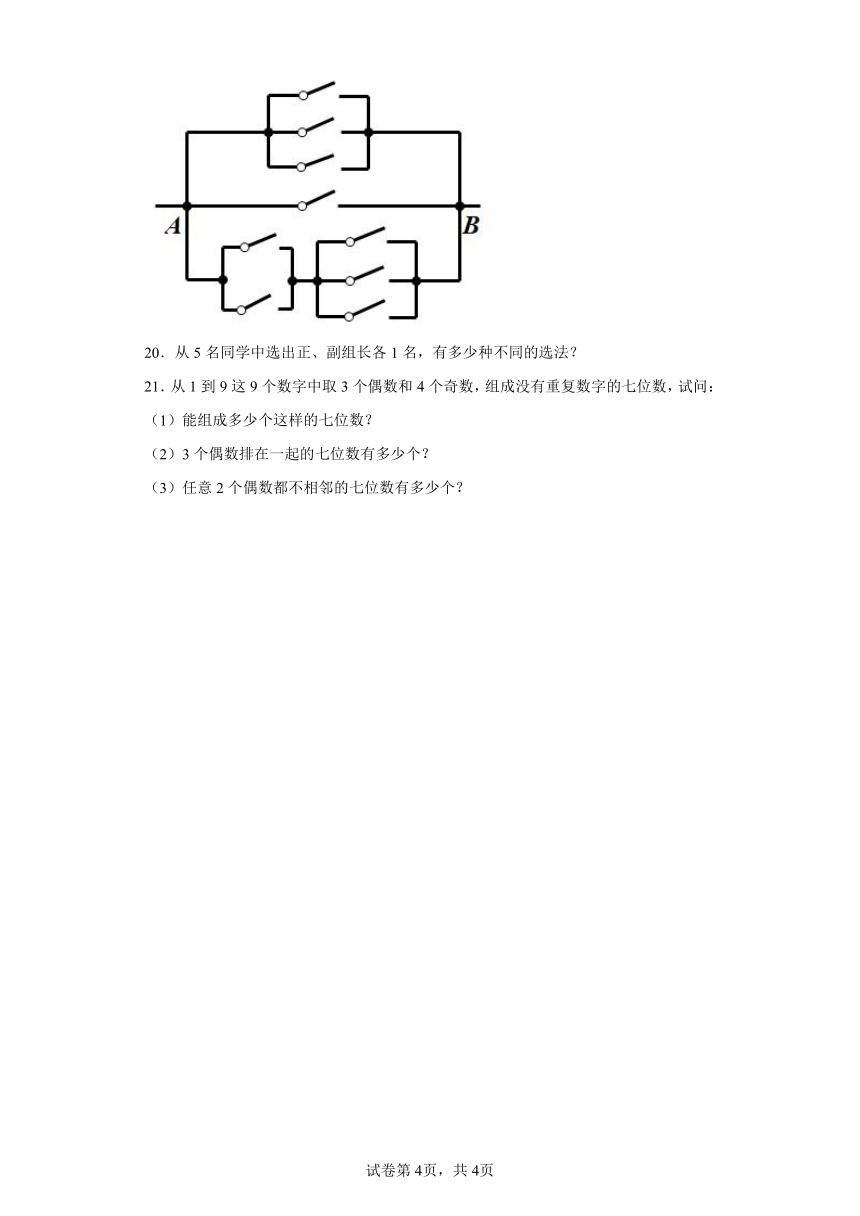
19.如图,一条电路从A处到B处接通时,可以有多少条不同的线路(每条线路仅含1条通路)?
20.从5名同学中选出正、副组长各1名,有多少种不同的选法?
21.从1到9这9个数字中取3个偶数和4个奇数,组成没有重复数字的七位数,试问:
(1)能组成多少个这样的七位数?
(2)3个偶数排在一起的七位数有多少个?
(3)任意2个偶数都不相邻的七位数有多少个?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
根据题意只需再从除甲、乙两位专家外的6人中选2人即可.
【详解】
解:由题意知,甲、乙已经被邀请,相当于只需再从6人中选2人,
则有种不同的组成方式.
故选:B.
2.B
利用分类加法原理求解即可.
【详解】
选女同学有3种选法,选男同学有2种选法,所以共有5种选法.
故选:B.
本题考查分类加法原理,是基础题.
3.B
利用分步计数原理,分3步即可求出
【详解】
解:由题意可知,分三步完成:
第一步,从2种主食中任选一种有2种选法;
第二步,从3种素菜中任选一种有3种选法;
第三步,从6种荤菜中任选一种有6种选法,
根据分步计数原理,共有不同的选取方法,
故选:B
4.A
求出所有涂色方法数为,再求出在任意两个有公共边的三角形所涂颜色不同的方法数,可先从中间一个三角形涂色,然后再涂其他三个三角形.
【详解】
5种颜色随机给如图所示的四块三角形区域涂色方法数为,
有公共边的三角形为同色,先考虑中间一块涂色有5种方法,其他三个三角形在剩下的4色中任意涂色均可,方法为,
所以所求概率为.
故选:A.
5.D
根据题意,分析“1药”和“1方”的取法数目,由分步计数原理计算可得答案.
【详解】
解:根据题意,某医生从“三药三方”中随机选出2种,恰好选出1药1方,
则1药的取法有3种,1方的取法也有3种,
则恰好选出1药1方的方法种数为;
故选:.
本题考查排列组合的应用,涉及分类计数原理的应用,属于基础题.
6.C
甲、乙要求相邻,则把甲和乙看成一个元素,与除去丙和丁以外的共4个元素进行全排列,其中甲和乙之间还有一个排列,根据丙和丁不相邻,把形成的五个空选两个排列丙和丁.得到结果.
【详解】
解:由题意知,
甲、乙要求相邻,则把甲和乙看成一个元素,
与除去丙和丁以外的共4个元素进行全排列,其中甲和乙之间还有一个排列,
把形成的五个空选两个排列丙和丁,
根据分步计数原理知共有A44A22A52=960种.
故选:C.
7.D
根据分步计数原理,结合限制条件,逐次排列,即可求解.
【详解】
根据分步计数原理,可得:
第一天可以是5个人中的任意一个,共有5种情形;
第二天除了第一天的那个人,另外4个人任意一个都可以,共有4种情形;
第三天除了第二天的那个人,另外4个人任意一个都可以,共有4种情形;
第四天除了第三天的那个人,另外4个人任意一个都可以,共有4种情形;
第五天除了第四天的那个人,另外4个人任意一个都可以,共有4种情形;
所以所有的排法总数为:种.
故选:D.
本题主要考查了分步计数原理的应用,其中解答中注意对限制条件的排列与遵循原则,属于基础题.
8.B
直接根据乘法原理计算得到答案.
【详解】
每个学生有3种选择,根据乘法原理共有种不同方法.
故选:.
本题考查了乘法原理,属于简单题.
9.B
按每一位算筹的根数分类,列举出所有的情况,根据根或根以上的算筹可以表示两个数字,计算出每种情况下所表示的三位数的个数,利用分类加法计数原理可得结果.
【详解】
按每一位算筹的根数分类一共有种情况,分别为、、、、、、、、、、、、、、,
根或根以上的算筹可以表示两个数字,运用分步乘法计数原理,得上面情况能表示的三位数字个数分别为:、、、、、、、、、、、、、、,
根据分类加法计数原理,得根算筹能表示的三位数字个数为:
.
故选:B.
10.D
先把5名同学分成组,有两种情况,再将他们分配下去即可求出.
【详解】
5名同学分成组,有两种情况,故共有种分组方式,再将他们分配到图书馆、食堂、学生活动中心有种方式,根据分步乘法计数原理可知,不同的安排方法共有种.
故选:D.
本题主要考查有限制条件的排列组合问题的解法应用,解题关键是对“至少”的处理,属于中档题.方法点睛:常见排列问题的求法有:
(1)相邻问题采取“捆绑法”;
(2)不相邻问题采取“插空法”;
(3)有限制元素采取“优先法”;
(4)特殊元素顺序确定问题,先让所有元素全排列,然后除以有限制元素的全排列数.
11.B
根据题意,子集和不可以互换,从子集分类讨论,结合计数原理,即可求解.
【详解】
由题意,对子集分类讨论:
当集合,集合可以是,共4种结果;
当集合,集合可以是,共2种结果;
当集合,集合可以是,共2种结果;
当集合,集合可以是,共1种结果,
根据计数原理,可得共有种结果.
故选:B.
本题主要考查了集合新定义及其应用,其中解答正确理解题意,结合集合子集的概念和计数原理进行解答值解答额关键,着重考查分析问题和解答问题的能力.
12.A
根据给定条件先求出“射”不在第一次的“六艺”讲座不同的次序数,去掉“射”不在第一次且“数”和“乐”两次相邻的“六艺”讲座不同的次序数即可得解.
【详解】
每周安排一次,共讲六次的“六艺”讲座活动,“射”不在第一次的不同次序数为,
其中“射”不在第一次且“数”和“乐”两次相邻的不同次序数为,
于是得,
所以“六艺”讲座不同的次序共有408种.
故选:A
思路点睛:含有两个限制条件的排列问题,利用排除法,先让一个条件被满足,再去掉这个条件满足时另一个条件不满足的所有可能即可解决问题.
13.128
根据分步乘法计数原理即可求出.
【详解】
∵学生只能从东门或西门进入校园,∴4名学生进入校园的方式共=16种.
∵教师只可以从南门或北门进入校园,∴3名教师进入校园的方式共有种.
∴3名教师和4名学生要进入校园的方式共有种情况.
故答案为:128.
14.6
根据不等式,结合三角形的性质,列举得到三角形的个数.
【详解】
时,;当时,,4;当时,,4,5.故这样的三角形共有(个).
故答案为:6
15.31
按两名学生的来源分三类,每一类分两步用分步乘法计数原理算出结果,再将所得结果相加即得.
【详解】
分为三类:甲、乙两班各选1名,有种选法;
甲、丙两班各选1名,有种选法;
乙、丙两班各选1名,有种选法,
由分类加法计数原理,得共有种推选方法.
故答案为:31
16.48
由已知按区域分四步,然后给,,,区域分步选择颜色,由此即可求解.
【详解】
解:由已知按区域分四步:第一步区域有4种选择,第二步区域有3种选择,
第三步区域有2种选择,第四步区域也有2种选择,
则由分步计数原理可得共有种,
故答案为:48.
17.36
按第一节上课的老师分成两类,利用分步乘法计数原理计算出每一类安排上课方法数,然后将两类方法数相加即得.
【详解】
不同的安排方案有两类办法:
第一类,第一节课若安排,则第四节课只能安排,第二节课从剩余4人中任选1人,第三节课从剩余3人中任选1人,共有种排法;
第二类,第一节课若安排,则第四节课可安排或,第二节课从剩余4人中任选1人,第三节课从剩余3人中任选1人,共有种排法,
因此不同的安排方案有种.
故答案为:36
18.80个
根据分步乘法计数原理计算出正确答案.
【详解】
在1~20中有2,3,5,7,11,13 ,17,19,共8个质数,
所以被减数有8种选法,减数在1~10中有10种选法,
根据分步乘法计数原理知,总共有(个)算式.
19.10
根据分步相乘和分类相加计数原理可得.
【详解】
从A处到B处接通,按上,中,下三类不同的方案:
上线路有3条;中线路有1条;下线路有条;
由分类加法计数原理知,从A处到B处接通共有 (条)不同的线路.
20.20种选法
从5人中依次选出正、副组长,由分步乘法计数原理即可得解.
【详解】
先从5人中选出一名组长,共有5种选法,
再从剩下的4人中选出一名副组长,共有4种选法,
所以从5名同学中选出正、副组长各1名,共有种选法.
21.(1);(2);(3).
(1)先选出符合要求的数,再全排列即可;
(2)利用捆绑法计算可得;
(2)先将4个奇数排好,再3个偶数插空,按照分步乘法计数原理计算可得;
【详解】
解:(1)分步完成:第一步,从4个偶数中取3个,有种情况;
第二步,从5个奇数中取4个,有种情况;
第三步,将取出的3个偶数和4个奇数进行全排列,有种情况.
所以符合题意的七位数的个数为.
(2)由题意,3个偶数排在一起的七位数的个数为
(3)由题意,可先把4个奇数排好,再将3个偶数分别插入5个空隙中,则符合题意的七位数的个数为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.某省专家组为评审某市是否达到“生态园林城市”的标准,从包含甲、乙两位专家在内的8人中选出4人组成评审委员会,若甲、乙两位专家已经被邀请,则组成该评审委员会的不同方式共有( )
A.30种 B.15种 C.20种 D.25种
2.从3名女同学和2名男同学中选1人主持主题班会,则不同的选法种数为( )
A.6 B.5 C.3 D.2
3.为响应国家“节约粮食”的号召,某同学决定在某食堂提供的2种主食、3种素菜、2种大荤、4种小荤中选取一种主食、一种素菜、一种荤菜作为今日伙食,并在用餐时积极践行“光盘行动”,则不同的选取方法有( )
A.48种 B.36种 C.24种 D.12种
4.用红,黄,蓝,绿,黑这5种颜色随机给如图所示的四块三角形区域涂色,则“在任意两个有公共边的三角形所涂颜色不同”的概率为( )
A. B. C. D.
5.今年我国中医药选出的“三药三方”对治疗新冠肺炎均有显著效果,功不可没.“三药”分别为金花清感颗粒、连花清瘟胶囊、血必清注射液;“三方”分别为清肺排毒汤、化湿败毒方、宜肺败毒方,若某医生从“三药三方”中随机选出2种,则恰好选出1药1方的方法种数为( )
A.15 B.30 C.6 D.9
6.7个人排成一排准备照一张合影,其中甲、乙要求相邻,丙、丁要求分开,则不同的排法有( )
A.480种 B.720种 C.960种 D.1200种
7.、、、、五人排一个5天的值日表,每天由一人值日,每人可以值多天或不值,但相邻的两天不能由同一人值,那么值日表的排法种数为( )
A.120 B.324 C.720 D.1280
8.4名学生报名参加语、数、英兴趣小组,每人选报1种,则不同方法有( )
A.种 B.种 C.种 D.种
9.算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如图:
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图;
如果把5根算筹以适当的方式全部放入下面的表格中,那么可以表示的三位数的个数为( )
A.46 B.44 C.42 D.40
10.把5名同学分配到图书馆、食堂、学生活动中心做志愿者,每个地方至少去一个同学,不同的安排方法共有( )种.
A.60 B.72 C.96 D.150
11.设,与是的子集,若,则称为一个“理想配集”.那么符合此条件的“理想配集”(规定与是两个不同的“理想配集”)的个数是( )
A.16 B.9 C.8 D.4
12.中园古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”主要指德育;“乐”主要指美育;“射”和“御”就是体育和劳动;“书”指各种历史文化知识;“数”指数学.某校国学社团开展“六艺”讲座活动,每周安排一次讲座,共讲六次.讲座次序要求“射”不在第一次,“数”和“乐”两次不相邻,则“六艺”讲座不同的次序共有( )
A.408种 B.240种 C.1092种. D.120种
二、填空题
13.某学校有东、南、西、北四个校门.受新冠肺炎疫情的影响,学校对进入四个校门做出如下规定:学生只能从东门或西门进入校园,教师只能从南门或北门进入校园.现有3名教师和4名学生要进入校园(不分先后顺序),请问进入校园的方式共有_________种.(用数字作答)
14.若三角形的三边长均为正整数,其中一边长为3,另外两边长分别为,,且满足,则这样的三角形有______个.
15.甲、乙、丙3个班各有3,5,2名三好学生,现准备推选2名来自不同班的三好学生去参加校三好学生代表大会,共有______种推选方法.
16.如图,用四种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法的种数为______(用数字作答)
17.某班一天上午有4节课,每节都需要安排一名教师去上课,现从,,,,,6名教师中安排4人分别上一节课,第一节课只能从,两人中安排一人,第四节课只能从,两人中安排一人,则不同的安排方案共有______种.(用数字作答)
三、解答题
18.从1~20中任选一个质数作为被减数,再从1~10中任选一个数作为减数,写成一个减法算式,共可得到多少个不同的算式?
19.如图,一条电路从A处到B处接通时,可以有多少条不同的线路(每条线路仅含1条通路)?
20.从5名同学中选出正、副组长各1名,有多少种不同的选法?
21.从1到9这9个数字中取3个偶数和4个奇数,组成没有重复数字的七位数,试问:
(1)能组成多少个这样的七位数?
(2)3个偶数排在一起的七位数有多少个?
(3)任意2个偶数都不相邻的七位数有多少个?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
根据题意只需再从除甲、乙两位专家外的6人中选2人即可.
【详解】
解:由题意知,甲、乙已经被邀请,相当于只需再从6人中选2人,
则有种不同的组成方式.
故选:B.
2.B
利用分类加法原理求解即可.
【详解】
选女同学有3种选法,选男同学有2种选法,所以共有5种选法.
故选:B.
本题考查分类加法原理,是基础题.
3.B
利用分步计数原理,分3步即可求出
【详解】
解:由题意可知,分三步完成:
第一步,从2种主食中任选一种有2种选法;
第二步,从3种素菜中任选一种有3种选法;
第三步,从6种荤菜中任选一种有6种选法,
根据分步计数原理,共有不同的选取方法,
故选:B
4.A
求出所有涂色方法数为,再求出在任意两个有公共边的三角形所涂颜色不同的方法数,可先从中间一个三角形涂色,然后再涂其他三个三角形.
【详解】
5种颜色随机给如图所示的四块三角形区域涂色方法数为,
有公共边的三角形为同色,先考虑中间一块涂色有5种方法,其他三个三角形在剩下的4色中任意涂色均可,方法为,
所以所求概率为.
故选:A.
5.D
根据题意,分析“1药”和“1方”的取法数目,由分步计数原理计算可得答案.
【详解】
解:根据题意,某医生从“三药三方”中随机选出2种,恰好选出1药1方,
则1药的取法有3种,1方的取法也有3种,
则恰好选出1药1方的方法种数为;
故选:.
本题考查排列组合的应用,涉及分类计数原理的应用,属于基础题.
6.C
甲、乙要求相邻,则把甲和乙看成一个元素,与除去丙和丁以外的共4个元素进行全排列,其中甲和乙之间还有一个排列,根据丙和丁不相邻,把形成的五个空选两个排列丙和丁.得到结果.
【详解】
解:由题意知,
甲、乙要求相邻,则把甲和乙看成一个元素,
与除去丙和丁以外的共4个元素进行全排列,其中甲和乙之间还有一个排列,
把形成的五个空选两个排列丙和丁,
根据分步计数原理知共有A44A22A52=960种.
故选:C.
7.D
根据分步计数原理,结合限制条件,逐次排列,即可求解.
【详解】
根据分步计数原理,可得:
第一天可以是5个人中的任意一个,共有5种情形;
第二天除了第一天的那个人,另外4个人任意一个都可以,共有4种情形;
第三天除了第二天的那个人,另外4个人任意一个都可以,共有4种情形;
第四天除了第三天的那个人,另外4个人任意一个都可以,共有4种情形;
第五天除了第四天的那个人,另外4个人任意一个都可以,共有4种情形;
所以所有的排法总数为:种.
故选:D.
本题主要考查了分步计数原理的应用,其中解答中注意对限制条件的排列与遵循原则,属于基础题.
8.B
直接根据乘法原理计算得到答案.
【详解】
每个学生有3种选择,根据乘法原理共有种不同方法.
故选:.
本题考查了乘法原理,属于简单题.
9.B
按每一位算筹的根数分类,列举出所有的情况,根据根或根以上的算筹可以表示两个数字,计算出每种情况下所表示的三位数的个数,利用分类加法计数原理可得结果.
【详解】
按每一位算筹的根数分类一共有种情况,分别为、、、、、、、、、、、、、、,
根或根以上的算筹可以表示两个数字,运用分步乘法计数原理,得上面情况能表示的三位数字个数分别为:、、、、、、、、、、、、、、,
根据分类加法计数原理,得根算筹能表示的三位数字个数为:
.
故选:B.
10.D
先把5名同学分成组,有两种情况,再将他们分配下去即可求出.
【详解】
5名同学分成组,有两种情况,故共有种分组方式,再将他们分配到图书馆、食堂、学生活动中心有种方式,根据分步乘法计数原理可知,不同的安排方法共有种.
故选:D.
本题主要考查有限制条件的排列组合问题的解法应用,解题关键是对“至少”的处理,属于中档题.方法点睛:常见排列问题的求法有:
(1)相邻问题采取“捆绑法”;
(2)不相邻问题采取“插空法”;
(3)有限制元素采取“优先法”;
(4)特殊元素顺序确定问题,先让所有元素全排列,然后除以有限制元素的全排列数.
11.B
根据题意,子集和不可以互换,从子集分类讨论,结合计数原理,即可求解.
【详解】
由题意,对子集分类讨论:
当集合,集合可以是,共4种结果;
当集合,集合可以是,共2种结果;
当集合,集合可以是,共2种结果;
当集合,集合可以是,共1种结果,
根据计数原理,可得共有种结果.
故选:B.
本题主要考查了集合新定义及其应用,其中解答正确理解题意,结合集合子集的概念和计数原理进行解答值解答额关键,着重考查分析问题和解答问题的能力.
12.A
根据给定条件先求出“射”不在第一次的“六艺”讲座不同的次序数,去掉“射”不在第一次且“数”和“乐”两次相邻的“六艺”讲座不同的次序数即可得解.
【详解】
每周安排一次,共讲六次的“六艺”讲座活动,“射”不在第一次的不同次序数为,
其中“射”不在第一次且“数”和“乐”两次相邻的不同次序数为,
于是得,
所以“六艺”讲座不同的次序共有408种.
故选:A
思路点睛:含有两个限制条件的排列问题,利用排除法,先让一个条件被满足,再去掉这个条件满足时另一个条件不满足的所有可能即可解决问题.
13.128
根据分步乘法计数原理即可求出.
【详解】
∵学生只能从东门或西门进入校园,∴4名学生进入校园的方式共=16种.
∵教师只可以从南门或北门进入校园,∴3名教师进入校园的方式共有种.
∴3名教师和4名学生要进入校园的方式共有种情况.
故答案为:128.
14.6
根据不等式,结合三角形的性质,列举得到三角形的个数.
【详解】
时,;当时,,4;当时,,4,5.故这样的三角形共有(个).
故答案为:6
15.31
按两名学生的来源分三类,每一类分两步用分步乘法计数原理算出结果,再将所得结果相加即得.
【详解】
分为三类:甲、乙两班各选1名,有种选法;
甲、丙两班各选1名,有种选法;
乙、丙两班各选1名,有种选法,
由分类加法计数原理,得共有种推选方法.
故答案为:31
16.48
由已知按区域分四步,然后给,,,区域分步选择颜色,由此即可求解.
【详解】
解:由已知按区域分四步:第一步区域有4种选择,第二步区域有3种选择,
第三步区域有2种选择,第四步区域也有2种选择,
则由分步计数原理可得共有种,
故答案为:48.
17.36
按第一节上课的老师分成两类,利用分步乘法计数原理计算出每一类安排上课方法数,然后将两类方法数相加即得.
【详解】
不同的安排方案有两类办法:
第一类,第一节课若安排,则第四节课只能安排,第二节课从剩余4人中任选1人,第三节课从剩余3人中任选1人,共有种排法;
第二类,第一节课若安排,则第四节课可安排或,第二节课从剩余4人中任选1人,第三节课从剩余3人中任选1人,共有种排法,
因此不同的安排方案有种.
故答案为:36
18.80个
根据分步乘法计数原理计算出正确答案.
【详解】
在1~20中有2,3,5,7,11,13 ,17,19,共8个质数,
所以被减数有8种选法,减数在1~10中有10种选法,
根据分步乘法计数原理知,总共有(个)算式.
19.10
根据分步相乘和分类相加计数原理可得.
【详解】
从A处到B处接通,按上,中,下三类不同的方案:
上线路有3条;中线路有1条;下线路有条;
由分类加法计数原理知,从A处到B处接通共有 (条)不同的线路.
20.20种选法
从5人中依次选出正、副组长,由分步乘法计数原理即可得解.
【详解】
先从5人中选出一名组长,共有5种选法,
再从剩下的4人中选出一名副组长,共有4种选法,
所以从5名同学中选出正、副组长各1名,共有种选法.
21.(1);(2);(3).
(1)先选出符合要求的数,再全排列即可;
(2)利用捆绑法计算可得;
(2)先将4个奇数排好,再3个偶数插空,按照分步乘法计数原理计算可得;
【详解】
解:(1)分步完成:第一步,从4个偶数中取3个,有种情况;
第二步,从5个奇数中取4个,有种情况;
第三步,将取出的3个偶数和4个奇数进行全排列,有种情况.
所以符合题意的七位数的个数为.
(2)由题意,3个偶数排在一起的七位数的个数为
(3)由题意,可先把4个奇数排好,再将3个偶数分别插入5个空隙中,则符合题意的七位数的个数为.
答案第1页,共2页
答案第1页,共2页
