1.2空间向量基本定理 同步练习(Word版含解析)
文档属性
| 名称 | 1.2空间向量基本定理 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 981.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 00:00:00 | ||
图片预览


文档简介
人教A版(2019)选择性必修第一册 1.2 空间向量基本定理 同步练习
一、单选题
1.在空间四点,,,中,若是空间的一个基底,则下列命题不正确的是( ).
A.,,,四点不共线 B.,,,四点共面,但不共线
C.,,,四点不共面 D.,,,点中任意三点不共线
2.下列说法正确的是( )
A.任何三个不共线的向量可构成空间向量的一个基底
B.空间的基底有且仅有一个
C.两两垂直的三个非零向量可构成空间的一个基底
D.基底中基向量与基底基向量对应相等
3.如图,在四面体OABC中,,,,点M在OA上,且,点N为BC的中点,则( ).
A. B.
C. D.
4.如图,已知空间四边形,其对角线为分别是的中点,点在线段上,且使,用向量表示向量为( )
A.
B.
C.
D.
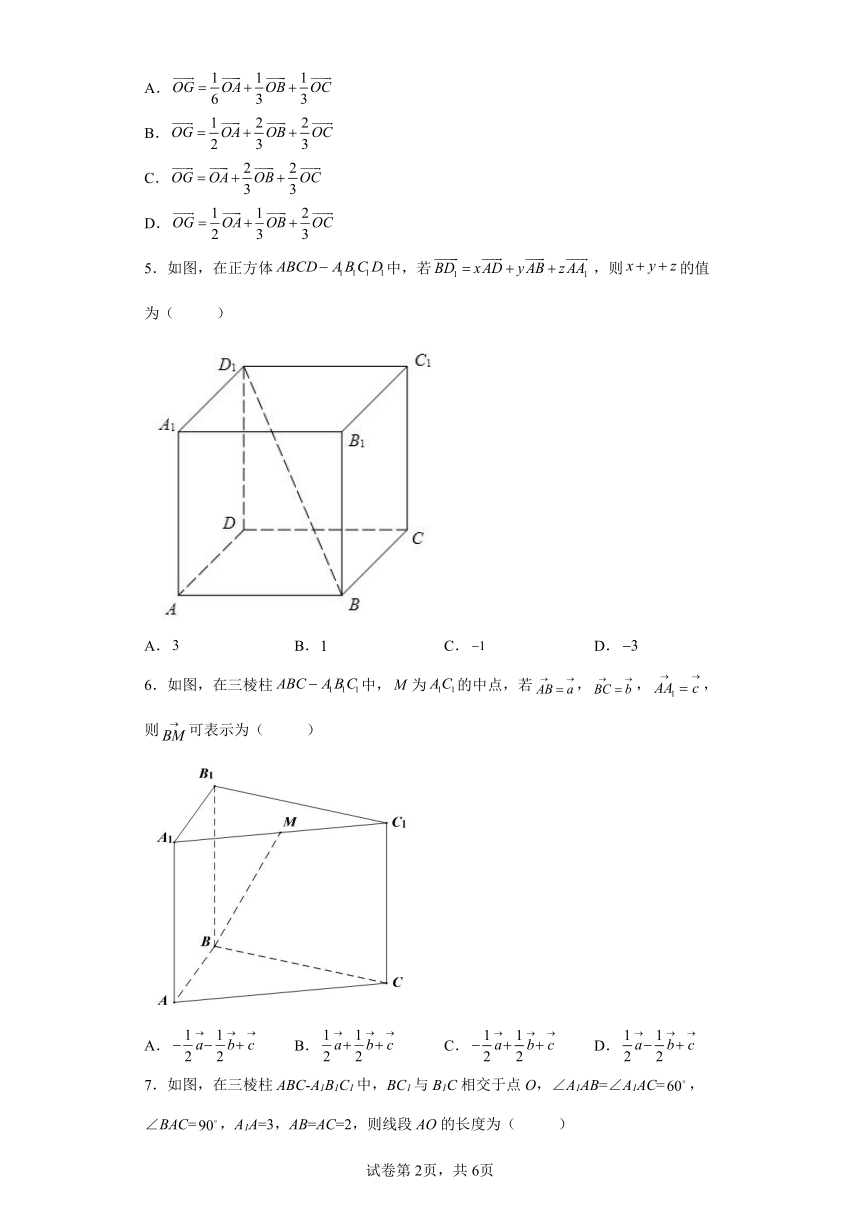
5.如图,在正方体中,若,则的值为( )
A. B. C. D.
6.如图,在三棱柱中,为的中点,若,,,则可表示为( )
A. B. C. D.
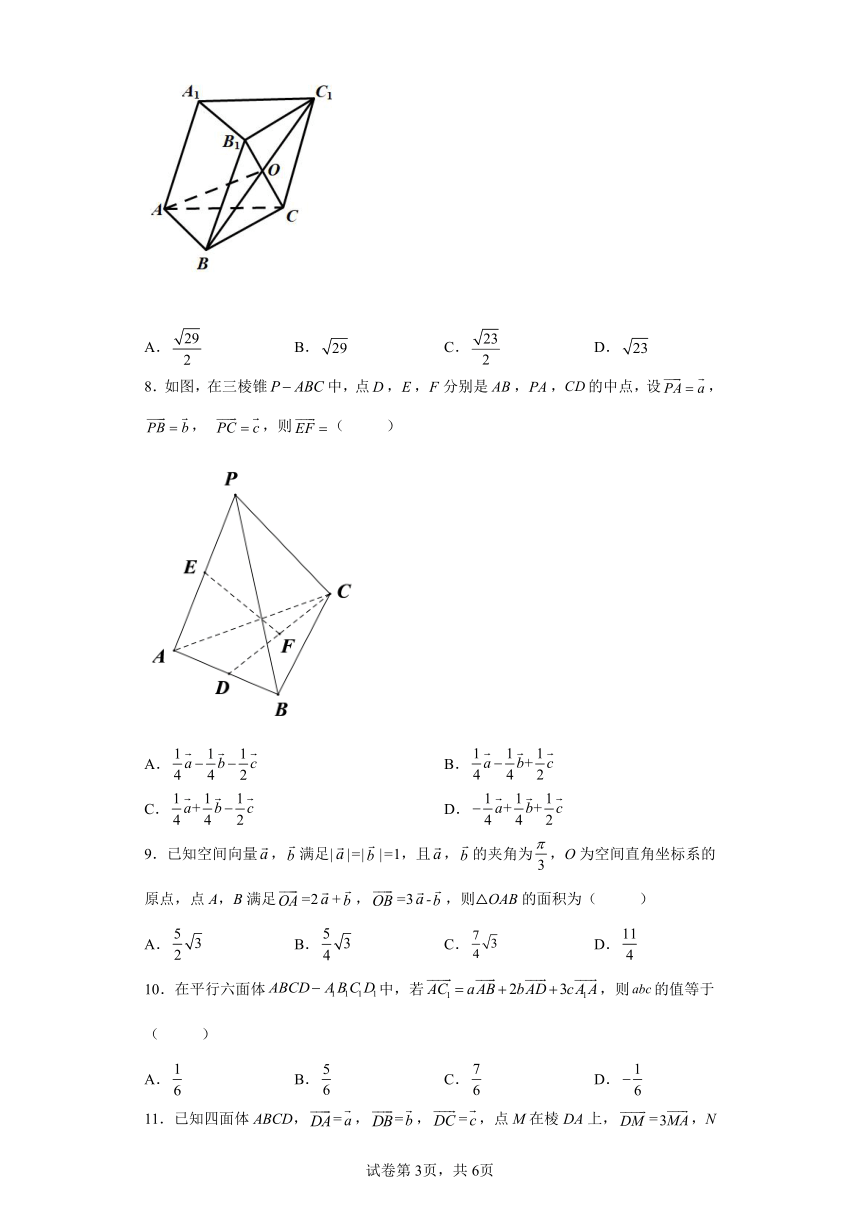
7.如图,在三棱柱ABC-A1B1C1中,BC1与B1C相交于点O,∠A1AB=∠A1AC=,∠BAC=,A1A=3,AB=AC=2,则线段AO的长度为( )
A. B. C. D.
8.如图,在三棱锥中,点,,分别是,,的中点,设,, ,则( )
A. B.
C. D.
9.已知空间向量,满足||=||=1,且,的夹角为,O为空间直角坐标系的原点,点A,B满足=2+,=3-,则△OAB的面积为( )
A. B. C. D.
10.在平行六面体中,若,则的值等于( )
A. B. C. D.
11.已知四面体ABCD,=,=,=,点M在棱DA上,=,N为BC中点,则=( )
A. B.
C. D.
12.下列能使向量,,成为空间的一个基底的关系式是( )
A. B.
C. D.
13.已知向量和在基底下的坐标分别为(3,4,5)和(0,2,1),若=,则向量在基底下的坐标是( )
A.
B.
C.
D.
14.在三棱柱中,是四边形的中心,,,,则( )
A. B.
C. D.
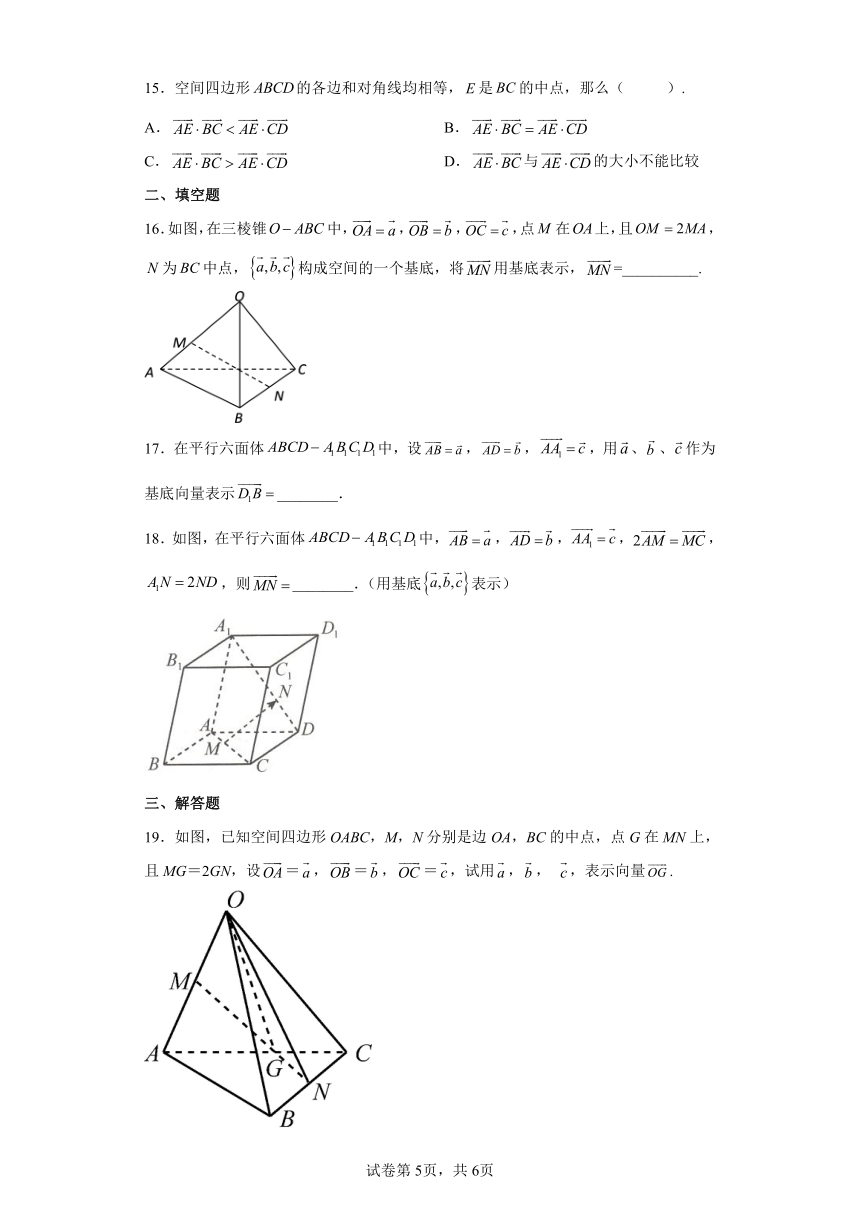
15.空间四边形的各边和对角线均相等,是的中点,那么( ).
A. B.
C. D.与的大小不能比较
二、填空题
16.如图,在三棱锥中,,,,点在上,且,为中点,构成空间的一个基底,将用基底表示,=__________.
17.在平行六面体中,设,,,用、、作为基底向量表示________.
18.如图,在平行六面体中,,,,,,则________.(用基底表示)
三、解答题
19.如图,已知空间四边形OABC,M,N分别是边OA,BC的中点,点G在MN上,且MG=2GN,设=,=,=,试用,, ,表示向量.
20.如图,已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为a的正方形,侧棱AA1长为b,且∠A1AB=∠A1AD=120°,求异面直线BD1和AC所成角的余弦值.
21.如图,在棱长为1的正方体中,E,F分别为,BD的中点,点G在CD上,且.
(1)求证:;
(2)求EF与CG所成角的余弦值.
22.已知四面体OABC,,.求证:.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
利用空间向量基底的定义依次判断即可
【详解】
选项A对应的命题是正确的,若四点共线,则向量,,共面,构不成基底;
选项B对应的命题是错误的,若四点共面,则,,共面,构不成基底;
选项C对应的命题是正确的,若四点共面,则,,构不成基底;
选项D对应的命题是正确的,若有三点共线,则这四点共面,向量,,构不成基底.
故选:B
此题考查空间向量的基底的定义,属于基础题
2.C
根据空间向量基本定理判断选项可解.
【详解】
项中应是不共面的三个向量构成空间向量的基底, 所以错.
项,空间基底有无数个, 所以错.
项中因为基底不唯一,所以错.
故选.
本题考查空间向量基本定理.
如果三个向量不共面,那么对空间任一向量,存在有序实数组使得
3.B
由向量的加法、减法及数乘运算法则计算即可.
【详解】
连接ON,则
由题可得
故选:B.
4.A
结合空间向量的加法、减法和数乘运算,把向量逐步向基底靠拢,再结合点的位置关系可得答案.
【详解】
.
因为分别为的中点,
所以
所以.
故选:A.
5.B
以为基底表示出,由此确定的值,进而求得的值.
【详解】
由题意可得,
∵,∴x=1,y=-1,z=1,故x+y+z=1,
故选:B
本小题主要考查用基底表示向量,考查空间向量基本定理,属于基础题.
6.C
结合图形,根据空间向量的线性运算即可得到答案.
【详解】
故选:C.
7.A
用表示出,计算,开方得出AO的长度.
【详解】
因为四边形是平行四边形,
,
,
,
,
,
即.
故选:A
8.D
利用空间向量的线性运算、三角形的中位线及线段中点的向量表示进行化简求解.
【详解】
如图,连接,
因为点,分别是,的中点,
所以.
因为点是的中点,
所以
.
因为点是的中点,
所以,
则.
故选:D.
9.B
求出和,cos∠AOB和sin∠AOB,根据三角形的面积公式可求出结果.
【详解】
||===,
||=,
则cos∠AOB===,
从而有sin∠AOB=,
∴△OAB的面积S=×××=,
故选:B.
10.D
根据条件用表示出,结合空间向量基本定理求出a,b,c即可.
【详解】
在平行六面体中,,如图,
则有,而,且不共面,
于是得,即,则,
的值等于
故选:D
11.C
根据给定条件用表示出,再借助向量加法法则即可得解.
【详解】
在四面体ABCD中,连接DN,如图所示,
=,=,=,因=,N为BC中点,则,,
于是得.
故选:C
12.C
根据平面向量基本定理及空间中四点共面的充要条件,逐一分析选项,即可得答案.
【详解】
对于A:由,可得M,A,B,C四点共面,即共面,
所以选项A无法构成基底,选项C可以构成基底;
对于B:因为,由平面向量基本定理,可得共面,无法构成基底,故B错误;
同理选项D中,共面,故D错误.
故选:C
13.A
根据向量的加减法运算可求得,再由=可求得,由此可得选项.
【详解】
解:因为=-
所以,所以向量在基底下的坐标是,
故选:A.
14.C
由向量线性运算依次推导即可得到结果.
【详解】
是四边形的中心,为中点,
.
故选:C.
15.C
空间四边形ABCD的各边及对角线均相等设为a,运用等边三角形的性质,可得,取BD的中点F,连接AF,EF,由余弦定理和向量的数量积的定义,计算可得,即可得到结论.
【详解】
空间四边形ABCD的各边及对角线均相等,设为a,E是边BC的中点,即有AE⊥BC,即,取BD的中点F,连接AF,EF,可得AF=AE=a,EF=a,
由余弦定理可得cos∠AEF=,可得与夹角的余弦值为,则,所以.
故选:C.
本题考查向量的数量积的运算和性质,运用向量垂直的条件和定义,以及余弦定理的运用,属于基础题.
16.
连接,根据向量的加减运算法则,求得,进而求得向量,得到答案.
【详解】
由题意,,,,
连接,根据向量的线性运算法则,可得,
因为为中点,,
又由点在上,且,可得,
所以.
17.
根据空间图形,根据向量加,减法的规则计算结果.
【详解】
有图形可知
.
故答案为:
18.
根据空间向量的线性运算求解.
【详解】
在平行六面体中
由题意,
,
所以
故答案为:.
19.
利用空间向量的线性运算及基本定理求解.
【详解】
因为M,N分别是边OA,BC的中点,点G在MN上,且MG=2GN,
,
,
,
,
.
20..
以作为空间的一个基底,结合题意,可用基底表示出,,分别求得,,,代入求夹角公式,即可得答案.
【详解】
因为两两不共线,所以可以作为空间的一个基底,
且,
又 ,
∴
=a2+b2+a2+2abcos 120°-0-2abcos 120°=2a2+b2,
∴.
又
=0+a2+abcos 120°+abcos 120°-a2-0=-ab.
∴
∴异面直线BD1和AC所成角的余弦值为 .
解题的关键是根据题意,确定基底,利用数量积公式、求模、求夹角公式求解,考查计算化简的能力.
21.(1)证明见解析;(2).
(1)建立空间直角坐标系,直接利用向量法证明;
(2)直接利用向量法求EF与CG所成角的余弦值
【详解】
(1)建立以D点为坐标原点,所在直线分别为轴,轴,轴建立空间直角坐标系,如图所示,
则,,,,
则,,
所以,即,
所以.
(2)由(1)知,,,
则,
因为EF与CG所成角的范围为,所以其夹角余弦值为.
22.证明见解析.
利用向量的运算,计算出,从而证明
【详解】
因为,
所以,
因为,,
所以,
所以,即.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.在空间四点,,,中,若是空间的一个基底,则下列命题不正确的是( ).
A.,,,四点不共线 B.,,,四点共面,但不共线
C.,,,四点不共面 D.,,,点中任意三点不共线
2.下列说法正确的是( )
A.任何三个不共线的向量可构成空间向量的一个基底
B.空间的基底有且仅有一个
C.两两垂直的三个非零向量可构成空间的一个基底
D.基底中基向量与基底基向量对应相等
3.如图,在四面体OABC中,,,,点M在OA上,且,点N为BC的中点,则( ).
A. B.
C. D.
4.如图,已知空间四边形,其对角线为分别是的中点,点在线段上,且使,用向量表示向量为( )
A.
B.
C.
D.
5.如图,在正方体中,若,则的值为( )
A. B. C. D.
6.如图,在三棱柱中,为的中点,若,,,则可表示为( )
A. B. C. D.
7.如图,在三棱柱ABC-A1B1C1中,BC1与B1C相交于点O,∠A1AB=∠A1AC=,∠BAC=,A1A=3,AB=AC=2,则线段AO的长度为( )
A. B. C. D.
8.如图,在三棱锥中,点,,分别是,,的中点,设,, ,则( )
A. B.
C. D.
9.已知空间向量,满足||=||=1,且,的夹角为,O为空间直角坐标系的原点,点A,B满足=2+,=3-,则△OAB的面积为( )
A. B. C. D.
10.在平行六面体中,若,则的值等于( )
A. B. C. D.
11.已知四面体ABCD,=,=,=,点M在棱DA上,=,N为BC中点,则=( )
A. B.
C. D.
12.下列能使向量,,成为空间的一个基底的关系式是( )
A. B.
C. D.
13.已知向量和在基底下的坐标分别为(3,4,5)和(0,2,1),若=,则向量在基底下的坐标是( )
A.
B.
C.
D.
14.在三棱柱中,是四边形的中心,,,,则( )
A. B.
C. D.
15.空间四边形的各边和对角线均相等,是的中点,那么( ).
A. B.
C. D.与的大小不能比较
二、填空题
16.如图,在三棱锥中,,,,点在上,且,为中点,构成空间的一个基底,将用基底表示,=__________.
17.在平行六面体中,设,,,用、、作为基底向量表示________.
18.如图,在平行六面体中,,,,,,则________.(用基底表示)
三、解答题
19.如图,已知空间四边形OABC,M,N分别是边OA,BC的中点,点G在MN上,且MG=2GN,设=,=,=,试用,, ,表示向量.
20.如图,已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为a的正方形,侧棱AA1长为b,且∠A1AB=∠A1AD=120°,求异面直线BD1和AC所成角的余弦值.
21.如图,在棱长为1的正方体中,E,F分别为,BD的中点,点G在CD上,且.
(1)求证:;
(2)求EF与CG所成角的余弦值.
22.已知四面体OABC,,.求证:.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
利用空间向量基底的定义依次判断即可
【详解】
选项A对应的命题是正确的,若四点共线,则向量,,共面,构不成基底;
选项B对应的命题是错误的,若四点共面,则,,共面,构不成基底;
选项C对应的命题是正确的,若四点共面,则,,构不成基底;
选项D对应的命题是正确的,若有三点共线,则这四点共面,向量,,构不成基底.
故选:B
此题考查空间向量的基底的定义,属于基础题
2.C
根据空间向量基本定理判断选项可解.
【详解】
项中应是不共面的三个向量构成空间向量的基底, 所以错.
项,空间基底有无数个, 所以错.
项中因为基底不唯一,所以错.
故选.
本题考查空间向量基本定理.
如果三个向量不共面,那么对空间任一向量,存在有序实数组使得
3.B
由向量的加法、减法及数乘运算法则计算即可.
【详解】
连接ON,则
由题可得
故选:B.
4.A
结合空间向量的加法、减法和数乘运算,把向量逐步向基底靠拢,再结合点的位置关系可得答案.
【详解】
.
因为分别为的中点,
所以
所以.
故选:A.
5.B
以为基底表示出,由此确定的值,进而求得的值.
【详解】
由题意可得,
∵,∴x=1,y=-1,z=1,故x+y+z=1,
故选:B
本小题主要考查用基底表示向量,考查空间向量基本定理,属于基础题.
6.C
结合图形,根据空间向量的线性运算即可得到答案.
【详解】
故选:C.
7.A
用表示出,计算,开方得出AO的长度.
【详解】
因为四边形是平行四边形,
,
,
,
,
,
即.
故选:A
8.D
利用空间向量的线性运算、三角形的中位线及线段中点的向量表示进行化简求解.
【详解】
如图,连接,
因为点,分别是,的中点,
所以.
因为点是的中点,
所以
.
因为点是的中点,
所以,
则.
故选:D.
9.B
求出和,cos∠AOB和sin∠AOB,根据三角形的面积公式可求出结果.
【详解】
||===,
||=,
则cos∠AOB===,
从而有sin∠AOB=,
∴△OAB的面积S=×××=,
故选:B.
10.D
根据条件用表示出,结合空间向量基本定理求出a,b,c即可.
【详解】
在平行六面体中,,如图,
则有,而,且不共面,
于是得,即,则,
的值等于
故选:D
11.C
根据给定条件用表示出,再借助向量加法法则即可得解.
【详解】
在四面体ABCD中,连接DN,如图所示,
=,=,=,因=,N为BC中点,则,,
于是得.
故选:C
12.C
根据平面向量基本定理及空间中四点共面的充要条件,逐一分析选项,即可得答案.
【详解】
对于A:由,可得M,A,B,C四点共面,即共面,
所以选项A无法构成基底,选项C可以构成基底;
对于B:因为,由平面向量基本定理,可得共面,无法构成基底,故B错误;
同理选项D中,共面,故D错误.
故选:C
13.A
根据向量的加减法运算可求得,再由=可求得,由此可得选项.
【详解】
解:因为=-
所以,所以向量在基底下的坐标是,
故选:A.
14.C
由向量线性运算依次推导即可得到结果.
【详解】
是四边形的中心,为中点,
.
故选:C.
15.C
空间四边形ABCD的各边及对角线均相等设为a,运用等边三角形的性质,可得,取BD的中点F,连接AF,EF,由余弦定理和向量的数量积的定义,计算可得,即可得到结论.
【详解】
空间四边形ABCD的各边及对角线均相等,设为a,E是边BC的中点,即有AE⊥BC,即,取BD的中点F,连接AF,EF,可得AF=AE=a,EF=a,
由余弦定理可得cos∠AEF=,可得与夹角的余弦值为,则,所以.
故选:C.
本题考查向量的数量积的运算和性质,运用向量垂直的条件和定义,以及余弦定理的运用,属于基础题.
16.
连接,根据向量的加减运算法则,求得,进而求得向量,得到答案.
【详解】
由题意,,,,
连接,根据向量的线性运算法则,可得,
因为为中点,,
又由点在上,且,可得,
所以.
17.
根据空间图形,根据向量加,减法的规则计算结果.
【详解】
有图形可知
.
故答案为:
18.
根据空间向量的线性运算求解.
【详解】
在平行六面体中
由题意,
,
所以
故答案为:.
19.
利用空间向量的线性运算及基本定理求解.
【详解】
因为M,N分别是边OA,BC的中点,点G在MN上,且MG=2GN,
,
,
,
,
.
20..
以作为空间的一个基底,结合题意,可用基底表示出,,分别求得,,,代入求夹角公式,即可得答案.
【详解】
因为两两不共线,所以可以作为空间的一个基底,
且,
又 ,
∴
=a2+b2+a2+2abcos 120°-0-2abcos 120°=2a2+b2,
∴.
又
=0+a2+abcos 120°+abcos 120°-a2-0=-ab.
∴
∴异面直线BD1和AC所成角的余弦值为 .
解题的关键是根据题意,确定基底,利用数量积公式、求模、求夹角公式求解,考查计算化简的能力.
21.(1)证明见解析;(2).
(1)建立空间直角坐标系,直接利用向量法证明;
(2)直接利用向量法求EF与CG所成角的余弦值
【详解】
(1)建立以D点为坐标原点,所在直线分别为轴,轴,轴建立空间直角坐标系,如图所示,
则,,,,
则,,
所以,即,
所以.
(2)由(1)知,,,
则,
因为EF与CG所成角的范围为,所以其夹角余弦值为.
22.证明见解析.
利用向量的运算,计算出,从而证明
【详解】
因为,
所以,
因为,,
所以,
所以,即.
答案第1页,共2页
答案第1页,共2页
