2020--2021学年冀教版数学七年级上册2.8平面图形的旋转 课件(共22张PPT)
文档属性
| 名称 | 2020--2021学年冀教版数学七年级上册2.8平面图形的旋转 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 10:44:30 | ||
图片预览








文档简介
(共22张PPT)
2.8平面图形的旋转
第二章 几何图形的初步认识
目标引领
1.通过观察具体实例认识旋转,理解旋转的基本含义;
2.探索旋转的基本性质;
⒊利用旋转的性质解决数学问题。
感受
荡秋千
转动的车轮
转动的时针
刮水器
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
在平面内,一个图形绕一个定点沿某个方向转过一个角度,这样的图形运动叫做旋转。
这个定点叫做 ,转过的这个角叫做 。
旋转的概念:
旋转中心
旋转角
O
P′
P
点0叫做旋转中心。
转动的角叫做旋转角
如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的对应点
总结
旋转的决定因素:旋转中心
( 三要素): 旋转角度
旋转方向
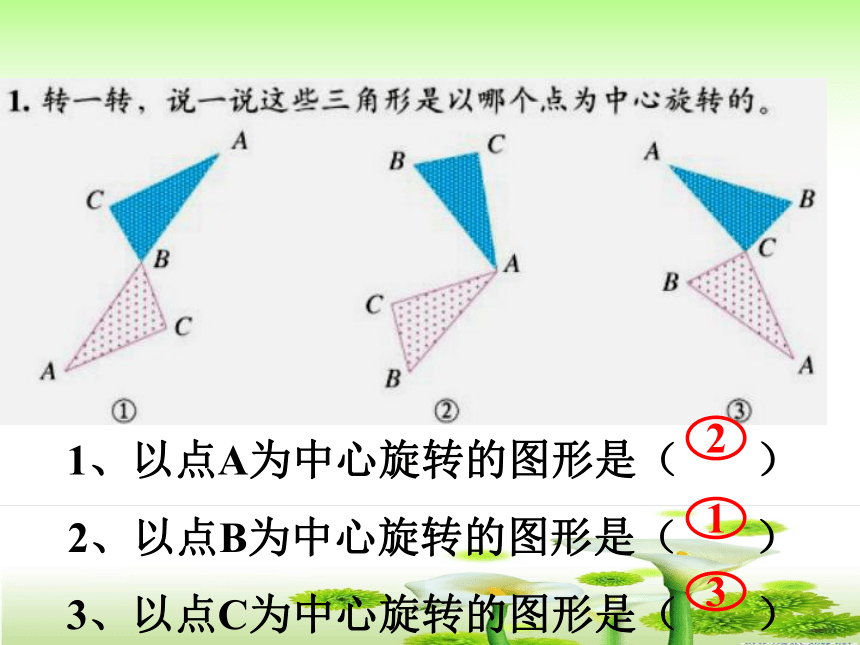
1、以点A为中心旋转的图形是( )
2、以点B为中心旋转的图形是( )
3、以点C为中心旋转的图形是( )
2
1
3
你理解了吗
2
3
180°
线段OB的对应线段是线段______
∠A的对应角是______
线段AB的对应线段是线段______
∠B的对应角是______
旋转中心是点______
旋转的角度是 ______
点B的对应点是点_____
3.下图, △A′OB′是△AOB绕点O按逆时针方向旋转45°所得的.则
B′
0B′
A′B′
∠A′
∠B′
O
45°
D′
D
A′
A
B
O
B′
旋转角
旋转中心
E
C
A
B
D
4、分别指出旋转中心和旋转角。
O
B
C
A
B’
C’
A’
1.如图,已知A,B是射线OM上的两点,且OA=1cm,OB=2.5cm.
(1)当OM旋转到ON位置时,点A,B分别旋转到点 A′,B′的位置,请画出点 A′,B′.
A′
B′
探究
A′
B′
(2) OA和OA′,OB和OB′分别有怎样的数量关系?
OA=OA′ ,OB=OB′
2.如图,三角形AOB绕点O按顺时针方向旋转后得到三角形COD,E是线段BA上一点.
(1)对应线段OB与OD,OA与OC,AB与CD都相等吗?
相等
探究
(2)∠BOD与∠AOC相等吗?
相等
(3)画出点E的对应点F.
方法一:用圆规以C点为圆心,以线段AE长为半径画弧,与CD交于点F.
方法二:用圆规以D为圆心,以线段BE长为半径画弧,与CD交于点F.
方法三:根据旋转角,通过射线旋转作出点F.
旋转的基本性质:
在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:
◆对应点到旋转中心的距离相等;
发现
◆每对对应点与旋转中心的连线所成的角都是相等的角,它们都等于旋转角。
新知应用
如图E是正方形ABCD内一点,将△ABE绕点B顺时针方向旋转到△CBF,其中EB=3cm,则BF=_____cm ,∠EBF=______
F
C
B
A
D
E
通过本节课的学习,请谈谈你有什么感受或收获?
你觉得还有什么疑惑
需要和大家探讨吗?
当堂检测
1.下列现象中属于旋转的有( )个.
①地下水位逐年下降; ②荡秋千; ③方向盘的转动; ④水龙头的转动; ⑤钟摆的运动; ⑥传送带的移动.
A.2 B.3 C.4 D.5
(1)旋转中心是点 .
(2)点A的对应点是 , 点B的对应
点是 , 点C的对应点是 ,
(3)写出图中的旋转角 。
2.如图,三角形ABC绕点O按逆时针方向旋转后得到三角形 .
3.如图所示的图案,如果最大圆的半径为2,
那么阴影部分面积是( )
A.π B.2π C.3π D.4π
C
O
B
1.基础作业:
87页,习题A、B组.
2.拓展作业:
本图案可以看做是菱形通过几次旋转得到的?每次旋转了多少度?
温馨提醒
2.8平面图形的旋转
第二章 几何图形的初步认识
目标引领
1.通过观察具体实例认识旋转,理解旋转的基本含义;
2.探索旋转的基本性质;
⒊利用旋转的性质解决数学问题。
感受
荡秋千
转动的车轮
转动的时针
刮水器
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?
在平面内,一个图形绕一个定点沿某个方向转过一个角度,这样的图形运动叫做旋转。
这个定点叫做 ,转过的这个角叫做 。
旋转的概念:
旋转中心
旋转角
O
P′
P
点0叫做旋转中心。
转动的角叫做旋转角
如果图形上的点P经过旋转变为点P′,那么这两个点P和P′叫做这个旋转的对应点
总结
旋转的决定因素:旋转中心
( 三要素): 旋转角度
旋转方向
1、以点A为中心旋转的图形是( )
2、以点B为中心旋转的图形是( )
3、以点C为中心旋转的图形是( )
2
1
3
你理解了吗
2
3
180°
线段OB的对应线段是线段______
∠A的对应角是______
线段AB的对应线段是线段______
∠B的对应角是______
旋转中心是点______
旋转的角度是 ______
点B的对应点是点_____
3.下图, △A′OB′是△AOB绕点O按逆时针方向旋转45°所得的.则
B′
0B′
A′B′
∠A′
∠B′
O
45°
D′
D
A′
A
B
O
B′
旋转角
旋转中心
E
C
A
B
D
4、分别指出旋转中心和旋转角。
O
B
C
A
B’
C’
A’
1.如图,已知A,B是射线OM上的两点,且OA=1cm,OB=2.5cm.
(1)当OM旋转到ON位置时,点A,B分别旋转到点 A′,B′的位置,请画出点 A′,B′.
A′
B′
探究
A′
B′
(2) OA和OA′,OB和OB′分别有怎样的数量关系?
OA=OA′ ,OB=OB′
2.如图,三角形AOB绕点O按顺时针方向旋转后得到三角形COD,E是线段BA上一点.
(1)对应线段OB与OD,OA与OC,AB与CD都相等吗?
相等
探究
(2)∠BOD与∠AOC相等吗?
相等
(3)画出点E的对应点F.
方法一:用圆规以C点为圆心,以线段AE长为半径画弧,与CD交于点F.
方法二:用圆规以D为圆心,以线段BE长为半径画弧,与CD交于点F.
方法三:根据旋转角,通过射线旋转作出点F.
旋转的基本性质:
在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:
◆对应点到旋转中心的距离相等;
发现
◆每对对应点与旋转中心的连线所成的角都是相等的角,它们都等于旋转角。
新知应用
如图E是正方形ABCD内一点,将△ABE绕点B顺时针方向旋转到△CBF,其中EB=3cm,则BF=_____cm ,∠EBF=______
F
C
B
A
D
E
通过本节课的学习,请谈谈你有什么感受或收获?
你觉得还有什么疑惑
需要和大家探讨吗?
当堂检测
1.下列现象中属于旋转的有( )个.
①地下水位逐年下降; ②荡秋千; ③方向盘的转动; ④水龙头的转动; ⑤钟摆的运动; ⑥传送带的移动.
A.2 B.3 C.4 D.5
(1)旋转中心是点 .
(2)点A的对应点是 , 点B的对应
点是 , 点C的对应点是 ,
(3)写出图中的旋转角 。
2.如图,三角形ABC绕点O按逆时针方向旋转后得到三角形 .
3.如图所示的图案,如果最大圆的半径为2,
那么阴影部分面积是( )
A.π B.2π C.3π D.4π
C
O
B
1.基础作业:
87页,习题A、B组.
2.拓展作业:
本图案可以看做是菱形通过几次旋转得到的?每次旋转了多少度?
温馨提醒
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
