八年级苏科版数学下册 9.3 平行四边形 课件(共19张PPT)
文档属性
| 名称 | 八年级苏科版数学下册 9.3 平行四边形 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 10:40:58 | ||
图片预览




文档简介
(共19张PPT)
平行四边形的判定1
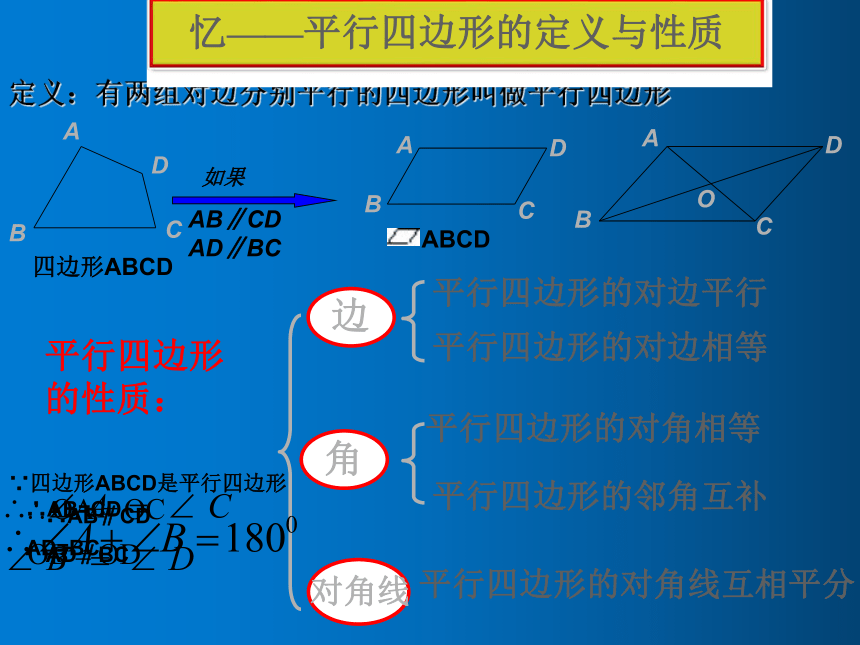
定义:有两组对边分别平行的四边形叫做平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
忆——平行四边形的定义与性质
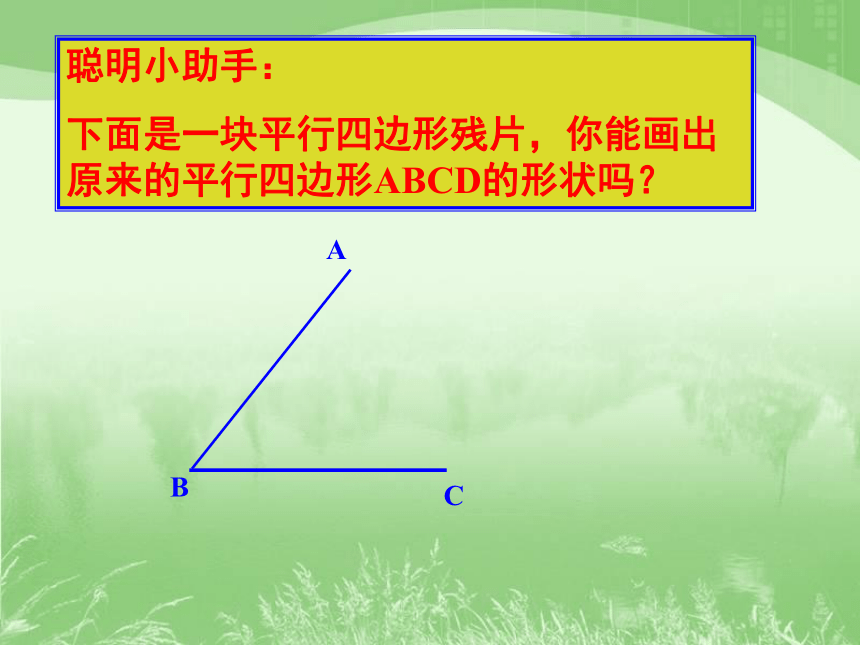
聪明小助手:
下面是一块平行四边形残片,你能画出原来的平行四边形ABCD的形状吗?
A
C
B
相信通过本节课的学习,你一定会解决这个问题!加油!
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
平行四边形的判定
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:原命题正确,逆命题一定正确吗?
猜一猜
平行四边形的对边相等
平行四边形的对角相等
平行四边形的对角线
互相平分
猜想1:
猜想2:
猜想3:
请根据平行四边形的定义来证明我们
在上面中得到的逆命题,由组长合理分工,
两人一组证明同一个逆命题,并在学案上
写出所选命题及命题的已知、求证和证明
过程,5分钟后班内展示,看哪一个小组完
成的又快又好。
小组交流与合作:
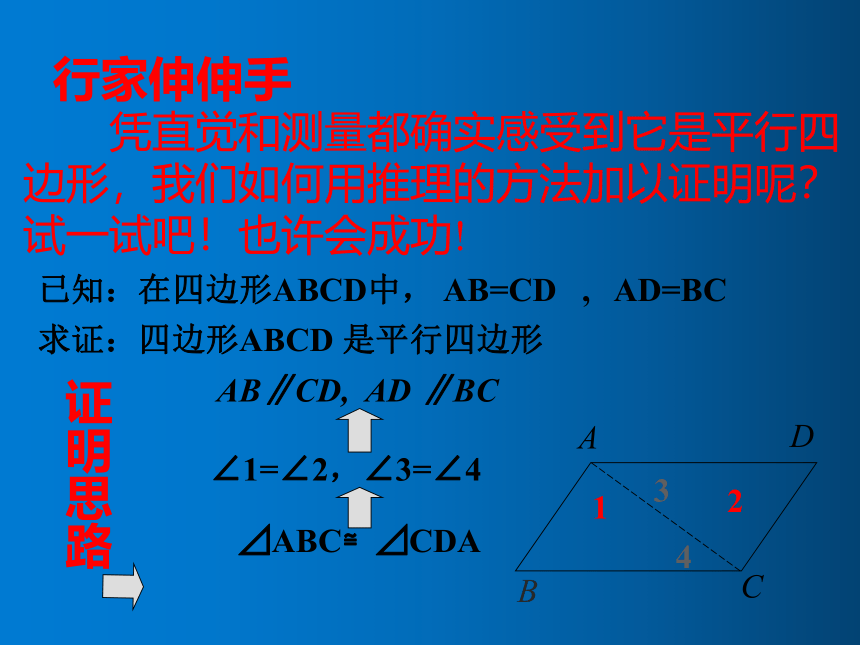
凭直觉和测量都确实感受到它是平行四边形,我们如何用推理的方法加以证明呢?试一试吧!也许会成功!
A
B
C
D
已知:在四边形ABCD中, AB=CD , AD=BC
求证:四边形ABCD 是平行四边形
证明思路
1
2
3
4
AB∥CD, AD ∥BC
∠1=∠2,∠3=∠4
⊿ABC≌⊿CDA
行家伸伸手
方法小结:有关四边形的问题常
常可转化为三角形问题来处理。
证明:连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
判定定理1:
猜想1
D
A
B
C
1
2
3
4
证一证
两组对角分别相等的四边形是平行四边形.
A
B
C
D
证明:
∴AB∥DC,AD∥BC
∠A+∠B+∠C+∠D=360°
已知:如图,在四边形ABCD中,∠A=∠C, ∠ B=∠D ,求证:四边形ABCD是平行四边形 .
在四边形ABCD中
∴四边形ABCD是平行四边形
∵∠A=∠C, ∠B=∠D
∴∠A+∠D=180°
∠A+∠B=180°
判定定理2
猜想2
已知:如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD.
∴△ADO ≌△CBO
OA=OC
证明:
OB=OD
∠AOD=∠COB
∴四边形ABCD是平行四边形
求证:四边形ABCD是平行四边形。
A
C
D
B
O
2
1
在△ADO 和△CBO中,
∴ ∠1=∠2
∴AD∥BC
同理 AB∥CD
对角线互相平分的四边形是平行四边形。
猜想3
判定定理3:
归纳升华
1、请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
⑴
⑶
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
⑵
D
4.8㎝
B
A
C
4.8㎝
7.6㎝
7.6㎝
抢答
如图,四边形ABCD对角线AC、BD相交于点O
⑴若AB∥CD,______,则得 ABCD;
⑵若AB=CD,______,则得 ABCD;
⑶若AC=8,BD=10,AO=4,_______,则得 ABCD
2、补充一个合适的条件使⑴—⑶小题成立:
3、 ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是OA、OC、OB、OD的中点,四边形EGFH___平行四边形。(填“是”或“不是”)
C
A
D
B
E
G
H
F
O
A
D
B
C
O
抢答
例 已知:平行四边形ABCD,对角线AC、BD相交于点O,E、F分别为OA、OC中点,求证:四边形BEDF是平行四边形。
证明:∵四边形ABCD是平行四边形
∴OA=OC,OB=OD(平行四边形的对角线互相平分)
∵E、F分别为OA、OC中点
∴OE= OA,,OF= OC
而OA=OC
∴OE=OF
又OB=OD
∴四边形BEDF是平行四边形(对角线互相平分的四边形是 平行四边形)
C
A
D
B
E
H
F
O
G
你还有其他的证明方法吗?
大显身手
已知:平行四边形ABCD,对角线AC、BD相交于点O,AE=CF,求证:四边BEDF是平行四边形。
还可以是:①AF=CE
②∠ADE=∠CBF
③∠CDE=∠ABF
④BE⊥AC,DF⊥AC
……
若将“E、F分别为OA、OC中点”改为“AE=CF”,四边形BEDF还是平行四边形吗?
试试看:你还能怎样改?
A
D
B
C
O
E
F
BE∥DF
变式训练
A
B
C
D
E
F
O
在上题中,若点E,F 分别在AC 两侧的延长线上,
如图,其他条件不变,结论还成立吗?请证明你的结论.
C
B
O
D
A
F
E
启示:
简便的证明方法
边,角
对角线
条件
拓展延伸
作AD∥BC,CD∥AB
聪明小助手
D
作AD=BC, CD=AB
A
B
C
D
A
B
C
连接AC,取AC中点O,连接BO并延长BO至D,使BO=DO
作:AC、BD互相平分
D
A
B
C
O
聪明小助手
任选教室里不坐在同一直线上的三个同学作为一个平行四边形的三个顶点,那么第四个顶点是哪个座位的同学,请你站起来。
小游戏:看谁反应快?
A
B
C
以三角形任两边为邻边作平行四边形可作3个。
A
D
B
C
D
A
B
C
A
B
C
D
课堂小结:
1、归纳一下本节课学行四边形的
判定方法共有哪些?
2、本节课我们用到了哪些数学思想方法?
平行四边形的判定1
定义:有两组对边分别平行的四边形叫做平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
忆——平行四边形的定义与性质
聪明小助手:
下面是一块平行四边形残片,你能画出原来的平行四边形ABCD的形状吗?
A
C
B
相信通过本节课的学习,你一定会解决这个问题!加油!
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
平行四边形的判定
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:原命题正确,逆命题一定正确吗?
猜一猜
平行四边形的对边相等
平行四边形的对角相等
平行四边形的对角线
互相平分
猜想1:
猜想2:
猜想3:
请根据平行四边形的定义来证明我们
在上面中得到的逆命题,由组长合理分工,
两人一组证明同一个逆命题,并在学案上
写出所选命题及命题的已知、求证和证明
过程,5分钟后班内展示,看哪一个小组完
成的又快又好。
小组交流与合作:
凭直觉和测量都确实感受到它是平行四边形,我们如何用推理的方法加以证明呢?试一试吧!也许会成功!
A
B
C
D
已知:在四边形ABCD中, AB=CD , AD=BC
求证:四边形ABCD 是平行四边形
证明思路
1
2
3
4
AB∥CD, AD ∥BC
∠1=∠2,∠3=∠4
⊿ABC≌⊿CDA
行家伸伸手
方法小结:有关四边形的问题常
常可转化为三角形问题来处理。
证明:连接BD.
∵ AB=CD,AD=BC,
BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
判定定理1:
猜想1
D
A
B
C
1
2
3
4
证一证
两组对角分别相等的四边形是平行四边形.
A
B
C
D
证明:
∴AB∥DC,AD∥BC
∠A+∠B+∠C+∠D=360°
已知:如图,在四边形ABCD中,∠A=∠C, ∠ B=∠D ,求证:四边形ABCD是平行四边形 .
在四边形ABCD中
∴四边形ABCD是平行四边形
∵∠A=∠C, ∠B=∠D
∴∠A+∠D=180°
∠A+∠B=180°
判定定理2
猜想2
已知:如图,在四边形ABCD中,AC与BD相交于点O,OA=OC,OB=OD.
∴△ADO ≌△CBO
OA=OC
证明:
OB=OD
∠AOD=∠COB
∴四边形ABCD是平行四边形
求证:四边形ABCD是平行四边形。
A
C
D
B
O
2
1
在△ADO 和△CBO中,
∴ ∠1=∠2
∴AD∥BC
同理 AB∥CD
对角线互相平分的四边形是平行四边形。
猜想3
判定定理3:
归纳升华
1、请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
⑴
⑶
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
⑵
D
4.8㎝
B
A
C
4.8㎝
7.6㎝
7.6㎝
抢答
如图,四边形ABCD对角线AC、BD相交于点O
⑴若AB∥CD,______,则得 ABCD;
⑵若AB=CD,______,则得 ABCD;
⑶若AC=8,BD=10,AO=4,_______,则得 ABCD
2、补充一个合适的条件使⑴—⑶小题成立:
3、 ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是OA、OC、OB、OD的中点,四边形EGFH___平行四边形。(填“是”或“不是”)
C
A
D
B
E
G
H
F
O
A
D
B
C
O
抢答
例 已知:平行四边形ABCD,对角线AC、BD相交于点O,E、F分别为OA、OC中点,求证:四边形BEDF是平行四边形。
证明:∵四边形ABCD是平行四边形
∴OA=OC,OB=OD(平行四边形的对角线互相平分)
∵E、F分别为OA、OC中点
∴OE= OA,,OF= OC
而OA=OC
∴OE=OF
又OB=OD
∴四边形BEDF是平行四边形(对角线互相平分的四边形是 平行四边形)
C
A
D
B
E
H
F
O
G
你还有其他的证明方法吗?
大显身手
已知:平行四边形ABCD,对角线AC、BD相交于点O,AE=CF,求证:四边BEDF是平行四边形。
还可以是:①AF=CE
②∠ADE=∠CBF
③∠CDE=∠ABF
④BE⊥AC,DF⊥AC
……
若将“E、F分别为OA、OC中点”改为“AE=CF”,四边形BEDF还是平行四边形吗?
试试看:你还能怎样改?
A
D
B
C
O
E
F
BE∥DF
变式训练
A
B
C
D
E
F
O
在上题中,若点E,F 分别在AC 两侧的延长线上,
如图,其他条件不变,结论还成立吗?请证明你的结论.
C
B
O
D
A
F
E
启示:
简便的证明方法
边,角
对角线
条件
拓展延伸
作AD∥BC,CD∥AB
聪明小助手
D
作AD=BC, CD=AB
A
B
C
D
A
B
C
连接AC,取AC中点O,连接BO并延长BO至D,使BO=DO
作:AC、BD互相平分
D
A
B
C
O
聪明小助手
任选教室里不坐在同一直线上的三个同学作为一个平行四边形的三个顶点,那么第四个顶点是哪个座位的同学,请你站起来。
小游戏:看谁反应快?
A
B
C
以三角形任两边为邻边作平行四边形可作3个。
A
D
B
C
D
A
B
C
A
B
C
D
课堂小结:
1、归纳一下本节课学行四边形的
判定方法共有哪些?
2、本节课我们用到了哪些数学思想方法?
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
