七年级苏科版下册7.1 探索直线平行的条件课件(共20张PPT)
文档属性
| 名称 | 七年级苏科版下册7.1 探索直线平行的条件课件(共20张PPT) | 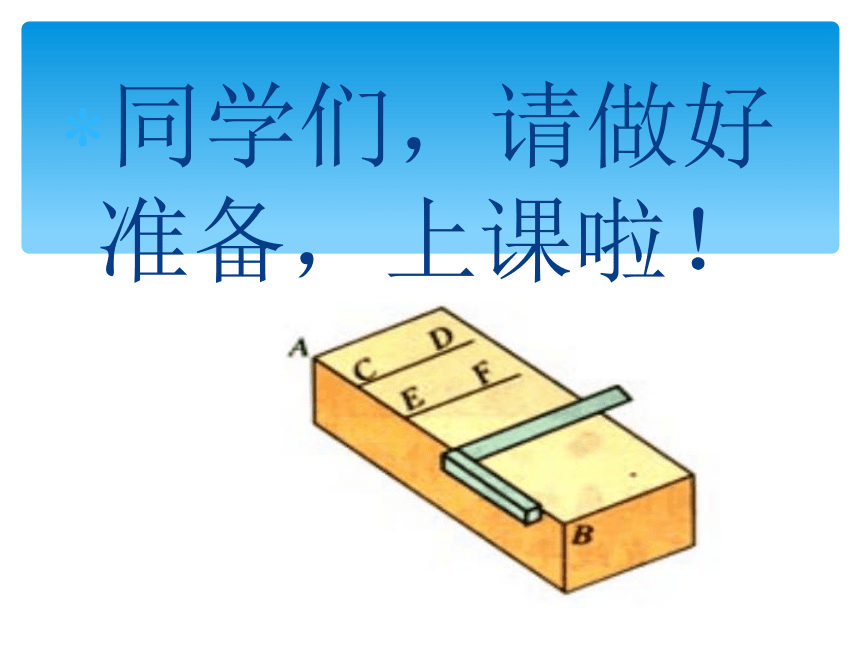 | |
| 格式 | ppt | ||
| 文件大小 | 761.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 11:00:48 | ||
图片预览



文档简介
(共20张PPT)
同学们,请做好准备,上课啦!
7.1 探索直线平行的条件
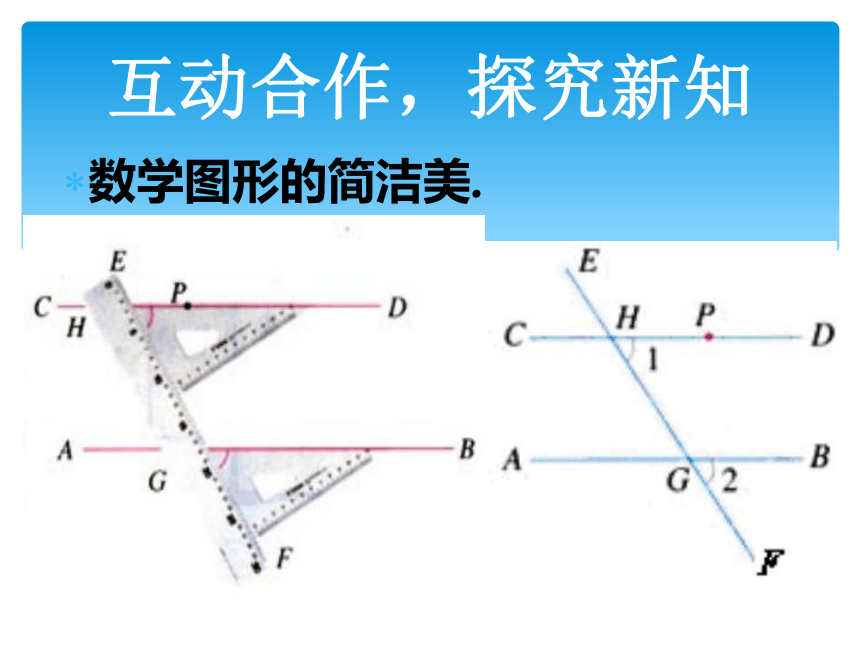
互动合作,探究新知
数学图形的简洁美.
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
判定方法1
1
2
a
A
B
C
D
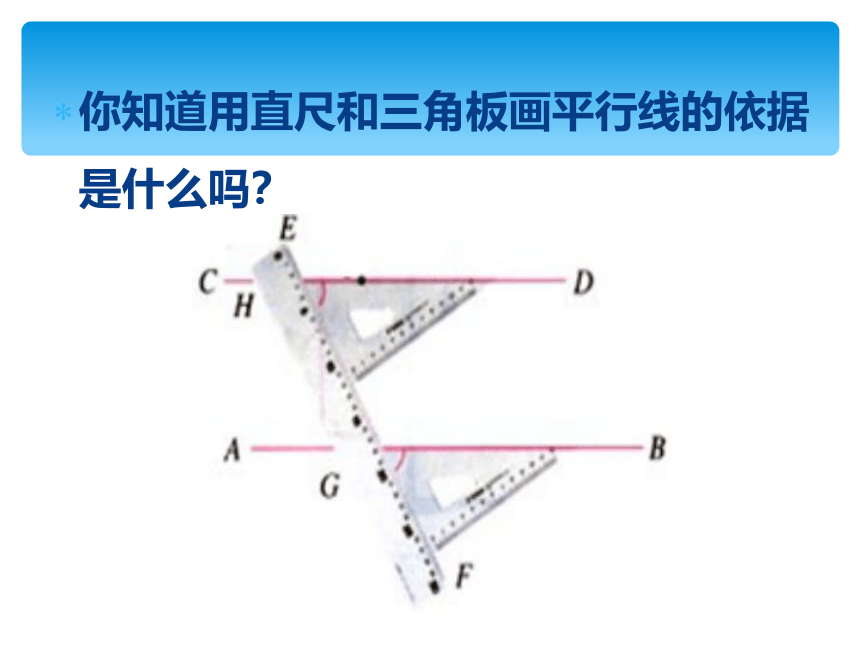
你知道用直尺和三角板画平行线的依据是什么吗?
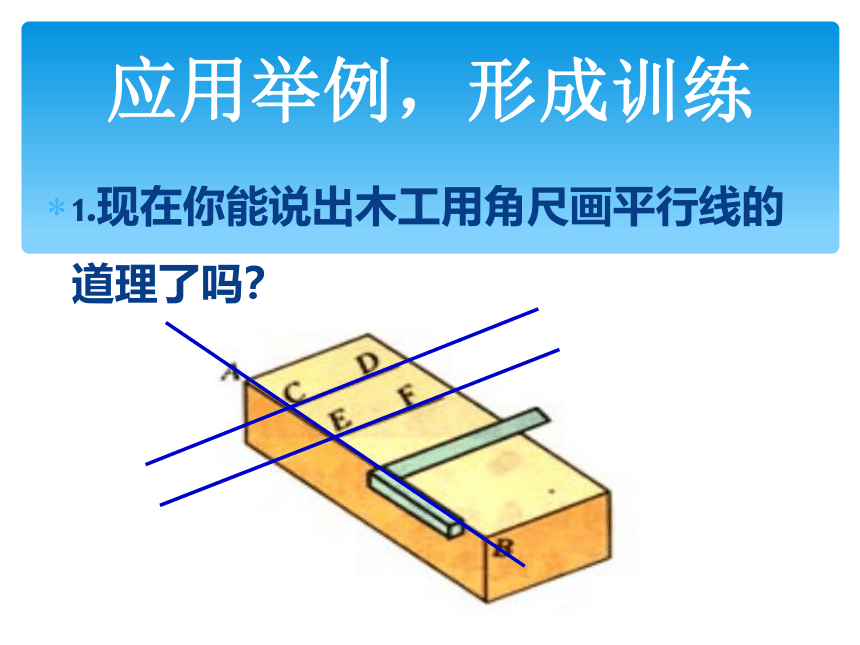
1.现在你能说出木工用角尺画平行线的道理了吗?
应用举例,形成训练
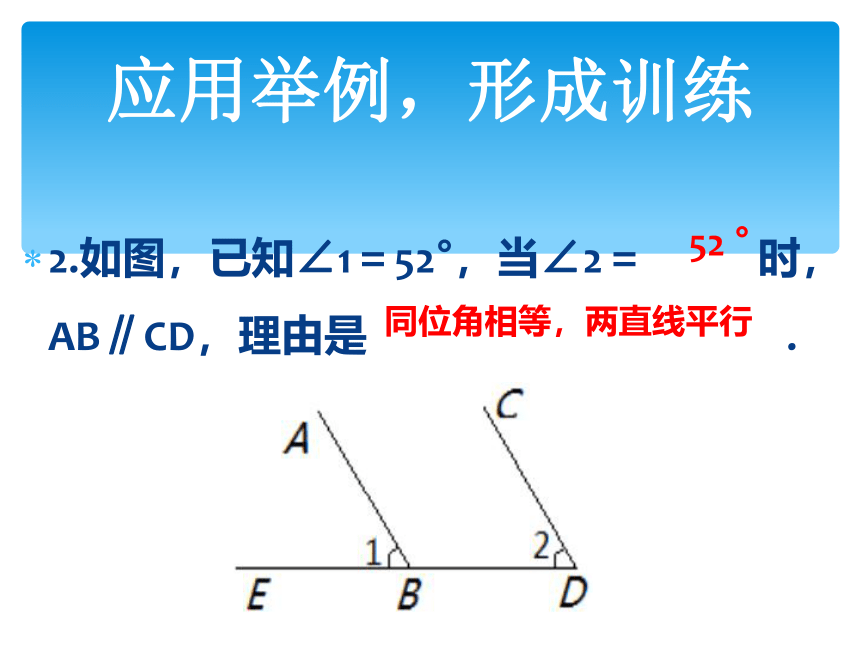
2.如图,已知∠1=52°,当∠2= 时,AB∥CD,理由是 .
应用举例,形成训练
52 °
同位角相等,两直线平行
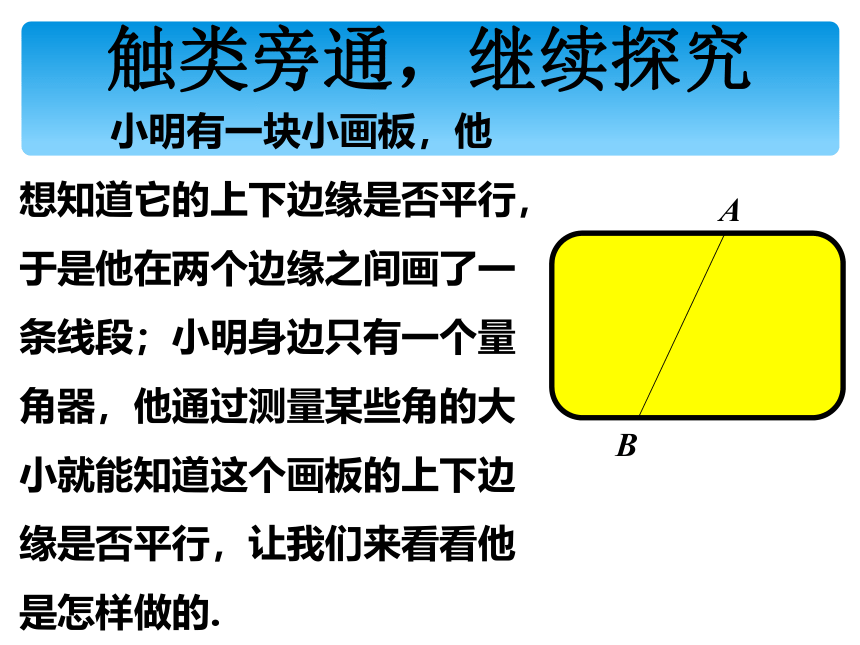
小明有一块小画板,他想知道它的上下边缘是否平行,于是他在两个边缘之间画了一条线段;小明身边只有一个量角器,他通过测量某些角的大小就能知道这个画板的上下边缘是否平行,让我们来看看他是怎样做的.
A
B
触类旁通,继续探究
A
B
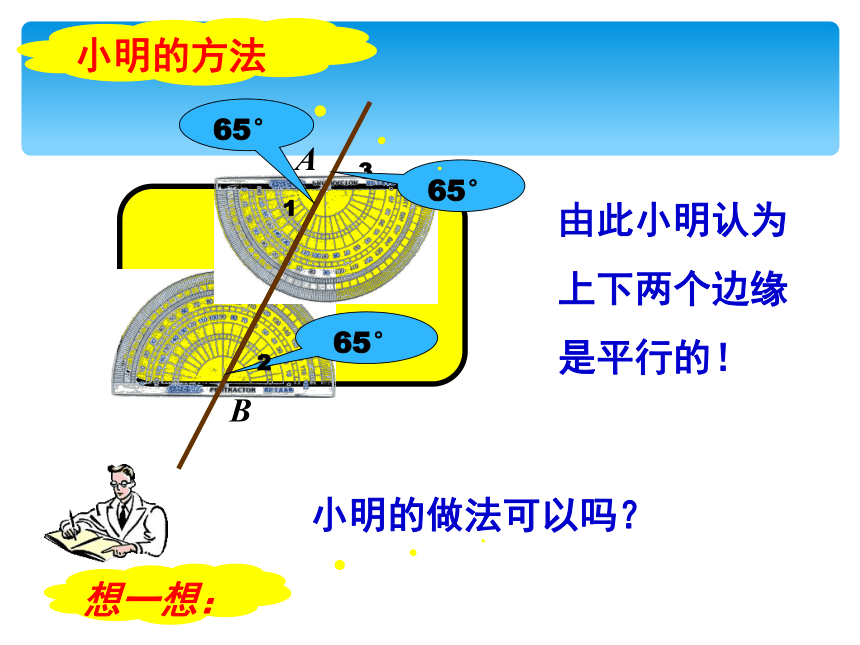
由此小明认为上下两个边缘是平行的!
65°
1
65°
2
想一想:
小明的做法可以吗?
3
65°
小明的方法
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
1
2
A
B
C
D
a
判定方法2
A
B
65°
2
115°
1
小丽的方法
想一想:
3
65°
同学们!你又想到其它判定直线平行的方法了吗?
如图,已知∠1+∠2=180°,试说明a∥b.
言之有据,规范说理
1
2
A
B
C
D
a
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
及时整理,归纳提升
例1 如图所示:(1)如果已知∠1=∠3,则可判定____∥____,其理由是________________________;
(2)如果已知∠4+∠5=180°,则可判定____∥____,其理由是__________________________;
(3)如果已知∠1=∠6,则
可判定____∥____,其理由
是______________________;
巩固新知,深化理解
AB
DE
同位角相等,两直线平行.
同旁内角互补,两直线平行.
BC
EF
AB
DE
内错角相等,两直线平行.
(4)如果已知∠5+∠2=180°,那么根据对顶角相等,有∠2=_____,因此可知∠4+∠5=______,所以可判定____∥____,其理由是_______________________.
趁热打铁,巩固新知
∠4
180°
BC
EF
同旁内角互补,两直线平行.
例2 在铺设铁轨时,两条直轨必须是互相平行的.如图,已经知道∠2是直角,那么再度量图中哪个角(图中已标出的),就可以判断两条直轨是否平行?说出你的理由.
巩固新知,深化理解
例3 如图,已知b⊥a,c⊥a,那么b与c平行吗?为什么?
巩固新知,深化理解
判定直线平行的三个方法:
①同位角相等,两直线平行;
②内错角相等,两直线平行;
③同旁内角互补,两直线平行.
通过“推理”的方式解决问题.
“转化”的数学思想方法.
归纳升华,畅谈收获
教材第16页习题5.2,第1、2、4、7题.
课堂延伸,布置作业
补充题:
已知:如图,直线AB、CD、EF被MN所截,∠1=∠2,∠3+∠1=180°,试说明CD∥EF.
同学们,请做好准备,上课啦!
7.1 探索直线平行的条件
互动合作,探究新知
数学图形的简洁美.
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
判定方法1
1
2
a
A
B
C
D
你知道用直尺和三角板画平行线的依据是什么吗?
1.现在你能说出木工用角尺画平行线的道理了吗?
应用举例,形成训练
2.如图,已知∠1=52°,当∠2= 时,AB∥CD,理由是 .
应用举例,形成训练
52 °
同位角相等,两直线平行
小明有一块小画板,他想知道它的上下边缘是否平行,于是他在两个边缘之间画了一条线段;小明身边只有一个量角器,他通过测量某些角的大小就能知道这个画板的上下边缘是否平行,让我们来看看他是怎样做的.
A
B
触类旁通,继续探究
A
B
由此小明认为上下两个边缘是平行的!
65°
1
65°
2
想一想:
小明的做法可以吗?
3
65°
小明的方法
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
1
2
A
B
C
D
a
判定方法2
A
B
65°
2
115°
1
小丽的方法
想一想:
3
65°
同学们!你又想到其它判定直线平行的方法了吗?
如图,已知∠1+∠2=180°,试说明a∥b.
言之有据,规范说理
1
2
A
B
C
D
a
判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
及时整理,归纳提升
例1 如图所示:(1)如果已知∠1=∠3,则可判定____∥____,其理由是________________________;
(2)如果已知∠4+∠5=180°,则可判定____∥____,其理由是__________________________;
(3)如果已知∠1=∠6,则
可判定____∥____,其理由
是______________________;
巩固新知,深化理解
AB
DE
同位角相等,两直线平行.
同旁内角互补,两直线平行.
BC
EF
AB
DE
内错角相等,两直线平行.
(4)如果已知∠5+∠2=180°,那么根据对顶角相等,有∠2=_____,因此可知∠4+∠5=______,所以可判定____∥____,其理由是_______________________.
趁热打铁,巩固新知
∠4
180°
BC
EF
同旁内角互补,两直线平行.
例2 在铺设铁轨时,两条直轨必须是互相平行的.如图,已经知道∠2是直角,那么再度量图中哪个角(图中已标出的),就可以判断两条直轨是否平行?说出你的理由.
巩固新知,深化理解
例3 如图,已知b⊥a,c⊥a,那么b与c平行吗?为什么?
巩固新知,深化理解
判定直线平行的三个方法:
①同位角相等,两直线平行;
②内错角相等,两直线平行;
③同旁内角互补,两直线平行.
通过“推理”的方式解决问题.
“转化”的数学思想方法.
归纳升华,畅谈收获
教材第16页习题5.2,第1、2、4、7题.
课堂延伸,布置作业
补充题:
已知:如图,直线AB、CD、EF被MN所截,∠1=∠2,∠3+∠1=180°,试说明CD∥EF.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
