七年级数学苏科版下册7.4 认识三角形 课件(共20张PPT)
文档属性
| 名称 | 七年级数学苏科版下册7.4 认识三角形 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1020.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
7.4 认识三角形(1)
认识三角形
1.定义:
3条不在同一条直线上的线段,
首尾依次相接组成图形。
书P22页
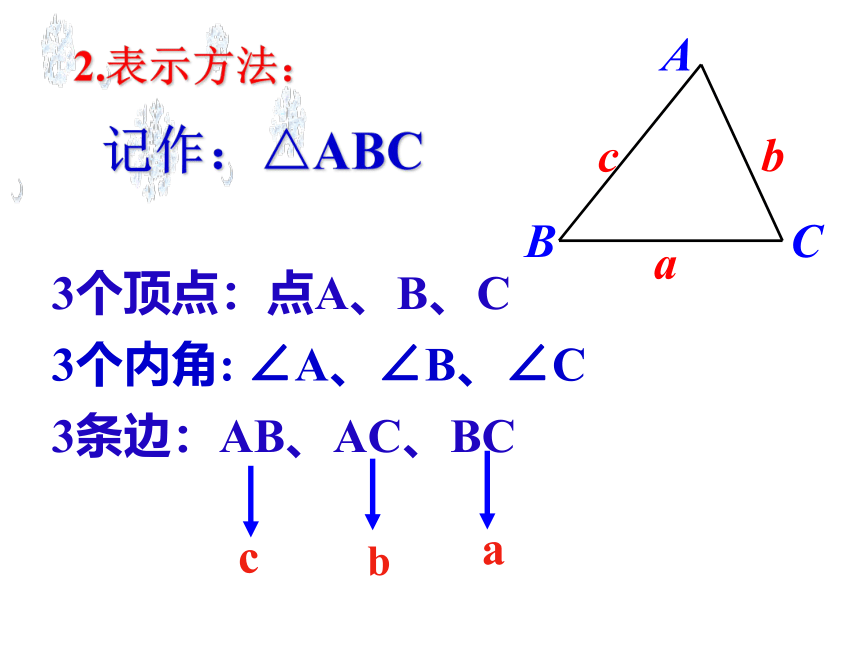
3个顶点:点A、B、C
3条边:AB、AC、BC
3个内角: ∠A、∠B、∠C
c
b
2.表示方法:
记作:△ABC
A
B
C
a
a
b
c
图中共有几个三角形?并表示出来。
A
B
C
D
E
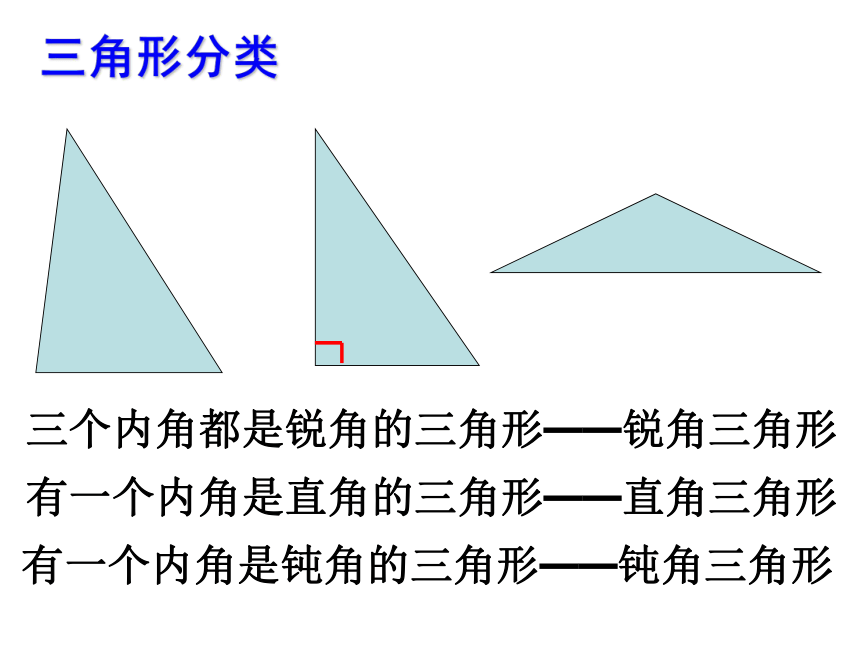
三个内角都是锐角的三角形——锐角三角形
有一个内角是直角的三角形——直角三角形
有一个内角是钝角的三角形——钝角三角形
三角形分类
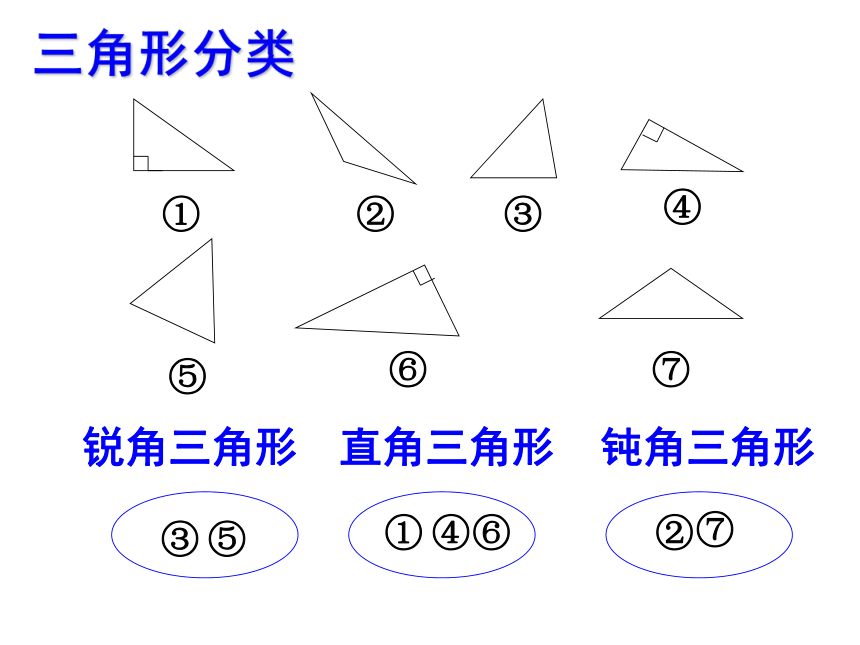
直角三角形
钝角三角形
⑦
②
①
③
④
⑤
⑥
①
②
③
④
⑤
⑥
⑦
三角形分类
锐角三角形
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
三边不等的三角形
等腰三角形
等边三角形
三角形分类
等边三角形是特殊的等腰三角形。
练一练
书P24页
【练一练】 1
【数学实验室】
从长度分别为3cm、4cm、5cm、6cm和9cm的
小木棒中任意取3根,能否搭成一个三角形?
可以搭几种不同的三角形?
发现三角形三边之间有怎样的关系?
书P23页
是不是任意三条线段都能组成一个三角形呢?
三角形的任意两边之和大于第三边。
根据“两点之间线段最短”,
可以得到: AB+AC > BC ,
同理可得: AC+BC > AB ,
AB+BC > AC .
三角形的三边关系:
A
B
C
延伸:
三角形的任意两边之差小于第三边。
2.三角形任意两边之差小于第三边。
3.三角形的第三边大于两边之差,小于两边之和。
1.三角形任意两边之和大于第三边。
三角形的三边关系:
练一练:
1、三条线段的长度分别为:
(1)3、8、10 (2)5、2、7
(3)5、5、11 (4)13、12、20
能组成三角形的有( )组。
A、1 B、2 C、3 D、4
技巧:
比较较小的两边之和与最长边的大小。
B
√
√
练一练:
2、有四根长度分别为3、5、7、10的木棒,
要摆出一个三角形,有( )种摆法。
A、1 B、2 C、3 D、4
B
课本P24 第2题
技巧:
三角形任意两边之和大于第三边。
练一练:
3.(1)若等腰三角形的两边分别为3㎝和5㎝,
那么周长为__________cm;
(2)若等腰三角形的两边分别为2㎝和5㎝,
那么周长为__________cm;
11或13
12
练一练:
4.有两根长度分别为4㎝和7㎝的木棒,
(1)再用一根长度为2㎝的木棒,
首尾相连,能组成三角形吗
用长度为11㎝的木棒呢 为什么?
(2)若第三边为x,则x在什么范围内
不能
不能
三角形任意两边之和大于第三边。
第三边大于3,且小于11。
表示为: 3练一练:
4.有两根长度分别为4㎝和7㎝的木棒,
(3)如果第三边是正整数,
那么第三边可能是哪几个数
(5)如果周长是奇数,那么第三边是多少?
(4)如果第三边是奇数呢?
∵ 3 < x < 11
∴ x = 4、5、6、7、8、9、10
x = 5、7、9
x = 4、6、8、10
本节课你有什么收获?
三角形的定义及表示方法。
三角形的分类(按内角分,按边分)
三角形的三边关系:
三角形的任意两边之和大于第三边。
三角形的任意两边之差小于第三边。
三角形第三边大于两边之差, 小于两边之和。
1.在△ABC中,AB=7,BC=3,AC为奇数,那么△ABC的周长为_______________.
2.若等腰△ABC周长为26,AB=6,那么它的腰长为_____________.
15
或17
或19
10
思考题
3.若等腰△ABC周长为20,AB=6,那么它的腰长为_____________.
6或7
7.4 认识三角形(1)
认识三角形
1.定义:
3条不在同一条直线上的线段,
首尾依次相接组成图形。
书P22页
3个顶点:点A、B、C
3条边:AB、AC、BC
3个内角: ∠A、∠B、∠C
c
b
2.表示方法:
记作:△ABC
A
B
C
a
a
b
c
图中共有几个三角形?并表示出来。
A
B
C
D
E
三个内角都是锐角的三角形——锐角三角形
有一个内角是直角的三角形——直角三角形
有一个内角是钝角的三角形——钝角三角形
三角形分类
直角三角形
钝角三角形
⑦
②
①
③
④
⑤
⑥
①
②
③
④
⑤
⑥
⑦
三角形分类
锐角三角形
三角形
按角分
锐角三角形
直角三角形
钝角三角形
按边分
三边不等的三角形
等腰三角形
等边三角形
三角形分类
等边三角形是特殊的等腰三角形。
练一练
书P24页
【练一练】 1
【数学实验室】
从长度分别为3cm、4cm、5cm、6cm和9cm的
小木棒中任意取3根,能否搭成一个三角形?
可以搭几种不同的三角形?
发现三角形三边之间有怎样的关系?
书P23页
是不是任意三条线段都能组成一个三角形呢?
三角形的任意两边之和大于第三边。
根据“两点之间线段最短”,
可以得到: AB+AC > BC ,
同理可得: AC+BC > AB ,
AB+BC > AC .
三角形的三边关系:
A
B
C
延伸:
三角形的任意两边之差小于第三边。
2.三角形任意两边之差小于第三边。
3.三角形的第三边大于两边之差,小于两边之和。
1.三角形任意两边之和大于第三边。
三角形的三边关系:
练一练:
1、三条线段的长度分别为:
(1)3、8、10 (2)5、2、7
(3)5、5、11 (4)13、12、20
能组成三角形的有( )组。
A、1 B、2 C、3 D、4
技巧:
比较较小的两边之和与最长边的大小。
B
√
√
练一练:
2、有四根长度分别为3、5、7、10的木棒,
要摆出一个三角形,有( )种摆法。
A、1 B、2 C、3 D、4
B
课本P24 第2题
技巧:
三角形任意两边之和大于第三边。
练一练:
3.(1)若等腰三角形的两边分别为3㎝和5㎝,
那么周长为__________cm;
(2)若等腰三角形的两边分别为2㎝和5㎝,
那么周长为__________cm;
11或13
12
练一练:
4.有两根长度分别为4㎝和7㎝的木棒,
(1)再用一根长度为2㎝的木棒,
首尾相连,能组成三角形吗
用长度为11㎝的木棒呢 为什么?
(2)若第三边为x,则x在什么范围内
不能
不能
三角形任意两边之和大于第三边。
第三边大于3,且小于11。
表示为: 3
4.有两根长度分别为4㎝和7㎝的木棒,
(3)如果第三边是正整数,
那么第三边可能是哪几个数
(5)如果周长是奇数,那么第三边是多少?
(4)如果第三边是奇数呢?
∵ 3 < x < 11
∴ x = 4、5、6、7、8、9、10
x = 5、7、9
x = 4、6、8、10
本节课你有什么收获?
三角形的定义及表示方法。
三角形的分类(按内角分,按边分)
三角形的三边关系:
三角形的任意两边之和大于第三边。
三角形的任意两边之差小于第三边。
三角形第三边大于两边之差, 小于两边之和。
1.在△ABC中,AB=7,BC=3,AC为奇数,那么△ABC的周长为_______________.
2.若等腰△ABC周长为26,AB=6,那么它的腰长为_____________.
15
或17
或19
10
思考题
3.若等腰△ABC周长为20,AB=6,那么它的腰长为_____________.
6或7
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
