2021--2022学年人教版七年级数学下册5.2.2平行线的判定第2课时课件(共27张PPT)
文档属性
| 名称 | 2021--2022学年人教版七年级数学下册5.2.2平行线的判定第2课时课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
5.2.2 平行线的判定2
1. 能根据“同位角相等,两直线平行”证明“同旁内角互补,两直线平行”“内错角相等,两直线平行”,并能简单地应用这些结论.
2. 初步了解证明的基本步骤和书写格式.
学习目标
重点:理解直线平行的判定方法,并会根据判定方法进行简单的推理应用;
难点:平行线判定方法的灵活运用和其推导过程中的转化思想的认识.
重难点
判定两直线平行的方法有哪些?
定义法.
平行公理的推论.
同位角相等,两直线平行.
新课导入
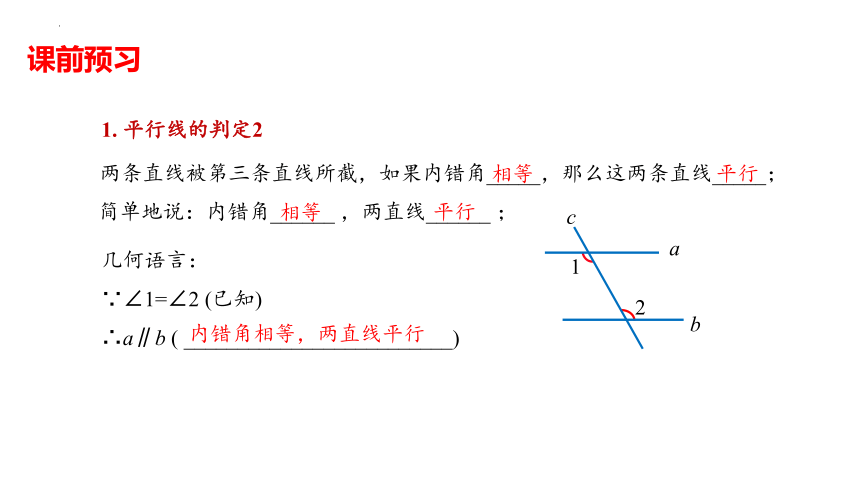
简单地说:内错角______ ,两直线______ ;
两条直线被第三条直线所截,如果内错角_____,那么这两条直线_____;
相等
平行
相等
平行
内错角相等,两直线平行
1. 平行线的判定2
几何语言:
∵∠1=∠2 (已知)
∴a∥b ( _________________________)
2
b
a
1
c
课前预习
两条直线被第三条直线所截,如果同旁内角______,那么这两条直线_____ ;
简单地说:同旁内角______ ,两直线______ ;
几何语言 :∵∠1+∠2=180°(已知)
∴AB∥CD (___________________________)
互补
平行
互补
平行
同旁内角互补,两直线平行
2. 平行线的判定方法3
2
b
a
1
c
课前预习
证明:∵AB⊥AC
∴∠_______=_____°(___________)
∵∠1=30°
∴∠BAD=∠______+∠____=______°
又∵∠B=60°
∴∠BAD+∠B=______°
∴AD∥BC (___________________________)
BAC
90
垂直的定义
BAC
1
120
180
同旁内角互补,两直线平行
1.如图,已知∠1=30°,∠B=60°,AB⊥AC,将证明AD∥BC的过程填写完整.
A
B
C
D
1
预习检测
两条直线被第三条直线所截,同时得到同位角、 内错角和同旁内角.由同位角相等,可以判定两条 直线平行,那么能否利用内错角来判定两条直线平行呢?
新知讲解
你能运用所学知识来证实它是一个真命题吗
猜想: 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
可以简单说成:内错角相等,两直线平行.
新知讲解
如图,如果∠2=∠3,能得出a∥b吗
分析:因为∠2=∠3,
而∠3=∠1(对顶角相等),
所以∠1=∠2,即同位角相等,
从而a∥b.
新知讲解
简单说成:内错角相等,两直线平行.
∵∠1=∠2,(已知)
∴a∥b. (内错角相等,两直线平行)
符号语言:
2
b
a
1
c
归纳总结
判定方法2
两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
例1 如图,BE是AB的延长线.
(1)由∠CBE=∠A可以判定哪两条直线平行?根据是什么?
(2)由∠CBE=∠C可以判定哪两条直线平行?根据是什么?
A
B
C
D
E
解:(1)由∠CBE=∠A可以判定AD∥BC.
根据是:同位角相等,两直线平行.
(2)由∠CBE=∠C可以判定AB∥CD.
根据是:内错角相等,两直线平行.
例题分析
②看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行.
利用内错角相等来判定两直线平行的方法
①看两角是不是两直线被第三条直线截得的角;
归纳总结
如图,已知∠ADE=60°,DF平分∠ADE,∠1=30°,试说明:DF∥BE.
巩固练习
解:∵DF平分∠ADE(已知),
∴∠EDF= ∠ADE(角平分线的定义).
又∵∠ADE=60°,
∴∠EDF=30°.
又∵∠1=30°(已知),
∴∠EDF=∠1,
∴DF∥BE(内错角相等,两直线平行) .
遇到一个新问题时,常常把它转化为已知的(或已解决的)问题. 这一节中,我们是怎样利用“同位角相等,两直线平行”得到“内错角相 等,两直线平行”的?你能利用“同位角相等,两直线平行”或“内错角相等,两直线平行”得到“同旁内角互补,两直线平行”吗?
新知讲解
分析:因为∠2+∠4=180°,
而∠1+∠4=180°(平角定义)
所以∠1=∠2,即同位角相等,
从而a∥b.
如图,如果∠2+∠4=180°,能得出a∥b吗
新知讲解
简单说成:同旁内角互补,两直线平行.
符号语言:
2
b
a
1
c
判定方法3
两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
∵∠1+∠2=180°,(已知)
∴a∥b. (同旁内角互补,两直线平行)
新知讲解
例2 如图,E 是 AB 上一点,F 是 DC 上一点,G 是 BC 延长线上一点. 如果∠D+∠DFE=180°,可以判定哪两条直线平行?为什么?
A
B
D
C
E
F
G
解:AD//EF,同旁内角互补,两直线平行.
例题分析
如图,直线AE,CD相交于点O,如果∠A=110°,∠1=70°,就可以说明AB∥CD,这是为什么?
巩固新知
解:因为∠1=∠AOD(对顶角相等) ,∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180° (等式的性质).
所以AB∥CD (同旁内角互补,两直线平行) .
a
b
c
1
2
平行线的判定方法
a
b
c
2
1
a
b
c
1
2
公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理:
同旁内角互补,两直线平行.
∵∠1+∠2=180°,∴ a∥b.
归纳总结
(中考·赤峰)如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC
B.BC∥CD
C.AB∥DC
D.AB与CD相交
C
链接中考
150°
30°
∠ABC+∠BCD=180°
AB∥DC
1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B B. ∠1=∠A
C. ∠3=∠B D. ∠3=∠A
1
2
3
A
E
B
C
D
C
2.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠4=180°,则a∥c
C
随堂检测
3.一学员在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次向右拐150 ,第二次向左拐30
B.第一次向左拐30 ,第二次向右拐30
C.第一次向右拐130 ,第二次向右拐50
D.第一次向左拐150 ,第二次向左拐30
B
30
30
随堂检测
4. (1)如图,若∠1=∠2,则_____∥ _____ ;若∠2=∠3,则_____ ∥_____.
(2)如图,若∠1=∠2,则_____ ∥ _____ ;
若∠3=∠4,则_____ ∥ _____.
AB
DE
BC
EF
BC
AB
CD
AD
随堂检测
5.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°. 找出图中的平行线,并说明理由.
解:OA∥BC,OB∥AC.
理由如下:
∵∠1=50°,∠2=50°,
∴∠1=∠2. ∴OB∥AC
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°.
∴OA∥BC.
随堂检测
2. 平行线的判定:
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补两直线平行.
课堂小结
1. 两条直线被第三条直线所截,会产生同位角、内错角、同旁内角. 角的关系决定了两条直线是否平行,因此在做题时要掌握好“三线八角”;
5.2.2 平行线的判定2
1. 能根据“同位角相等,两直线平行”证明“同旁内角互补,两直线平行”“内错角相等,两直线平行”,并能简单地应用这些结论.
2. 初步了解证明的基本步骤和书写格式.
学习目标
重点:理解直线平行的判定方法,并会根据判定方法进行简单的推理应用;
难点:平行线判定方法的灵活运用和其推导过程中的转化思想的认识.
重难点
判定两直线平行的方法有哪些?
定义法.
平行公理的推论.
同位角相等,两直线平行.
新课导入
简单地说:内错角______ ,两直线______ ;
两条直线被第三条直线所截,如果内错角_____,那么这两条直线_____;
相等
平行
相等
平行
内错角相等,两直线平行
1. 平行线的判定2
几何语言:
∵∠1=∠2 (已知)
∴a∥b ( _________________________)
2
b
a
1
c
课前预习
两条直线被第三条直线所截,如果同旁内角______,那么这两条直线_____ ;
简单地说:同旁内角______ ,两直线______ ;
几何语言 :∵∠1+∠2=180°(已知)
∴AB∥CD (___________________________)
互补
平行
互补
平行
同旁内角互补,两直线平行
2. 平行线的判定方法3
2
b
a
1
c
课前预习
证明:∵AB⊥AC
∴∠_______=_____°(___________)
∵∠1=30°
∴∠BAD=∠______+∠____=______°
又∵∠B=60°
∴∠BAD+∠B=______°
∴AD∥BC (___________________________)
BAC
90
垂直的定义
BAC
1
120
180
同旁内角互补,两直线平行
1.如图,已知∠1=30°,∠B=60°,AB⊥AC,将证明AD∥BC的过程填写完整.
A
B
C
D
1
预习检测
两条直线被第三条直线所截,同时得到同位角、 内错角和同旁内角.由同位角相等,可以判定两条 直线平行,那么能否利用内错角来判定两条直线平行呢?
新知讲解
你能运用所学知识来证实它是一个真命题吗
猜想: 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
可以简单说成:内错角相等,两直线平行.
新知讲解
如图,如果∠2=∠3,能得出a∥b吗
分析:因为∠2=∠3,
而∠3=∠1(对顶角相等),
所以∠1=∠2,即同位角相等,
从而a∥b.
新知讲解
简单说成:内错角相等,两直线平行.
∵∠1=∠2,(已知)
∴a∥b. (内错角相等,两直线平行)
符号语言:
2
b
a
1
c
归纳总结
判定方法2
两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
例1 如图,BE是AB的延长线.
(1)由∠CBE=∠A可以判定哪两条直线平行?根据是什么?
(2)由∠CBE=∠C可以判定哪两条直线平行?根据是什么?
A
B
C
D
E
解:(1)由∠CBE=∠A可以判定AD∥BC.
根据是:同位角相等,两直线平行.
(2)由∠CBE=∠C可以判定AB∥CD.
根据是:内错角相等,两直线平行.
例题分析
②看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行.
利用内错角相等来判定两直线平行的方法
①看两角是不是两直线被第三条直线截得的角;
归纳总结
如图,已知∠ADE=60°,DF平分∠ADE,∠1=30°,试说明:DF∥BE.
巩固练习
解:∵DF平分∠ADE(已知),
∴∠EDF= ∠ADE(角平分线的定义).
又∵∠ADE=60°,
∴∠EDF=30°.
又∵∠1=30°(已知),
∴∠EDF=∠1,
∴DF∥BE(内错角相等,两直线平行) .
遇到一个新问题时,常常把它转化为已知的(或已解决的)问题. 这一节中,我们是怎样利用“同位角相等,两直线平行”得到“内错角相 等,两直线平行”的?你能利用“同位角相等,两直线平行”或“内错角相等,两直线平行”得到“同旁内角互补,两直线平行”吗?
新知讲解
分析:因为∠2+∠4=180°,
而∠1+∠4=180°(平角定义)
所以∠1=∠2,即同位角相等,
从而a∥b.
如图,如果∠2+∠4=180°,能得出a∥b吗
新知讲解
简单说成:同旁内角互补,两直线平行.
符号语言:
2
b
a
1
c
判定方法3
两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
∵∠1+∠2=180°,(已知)
∴a∥b. (同旁内角互补,两直线平行)
新知讲解
例2 如图,E 是 AB 上一点,F 是 DC 上一点,G 是 BC 延长线上一点. 如果∠D+∠DFE=180°,可以判定哪两条直线平行?为什么?
A
B
D
C
E
F
G
解:AD//EF,同旁内角互补,两直线平行.
例题分析
如图,直线AE,CD相交于点O,如果∠A=110°,∠1=70°,就可以说明AB∥CD,这是为什么?
巩固新知
解:因为∠1=∠AOD(对顶角相等) ,∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180° (等式的性质).
所以AB∥CD (同旁内角互补,两直线平行) .
a
b
c
1
2
平行线的判定方法
a
b
c
2
1
a
b
c
1
2
公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理:
同旁内角互补,两直线平行.
∵∠1+∠2=180°,∴ a∥b.
归纳总结
(中考·赤峰)如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC
B.BC∥CD
C.AB∥DC
D.AB与CD相交
C
链接中考
150°
30°
∠ABC+∠BCD=180°
AB∥DC
1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B B. ∠1=∠A
C. ∠3=∠B D. ∠3=∠A
1
2
3
A
E
B
C
D
C
2.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠4=180°,则a∥c
C
随堂检测
3.一学员在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次向右拐150 ,第二次向左拐30
B.第一次向左拐30 ,第二次向右拐30
C.第一次向右拐130 ,第二次向右拐50
D.第一次向左拐150 ,第二次向左拐30
B
30
30
随堂检测
4. (1)如图,若∠1=∠2,则_____∥ _____ ;若∠2=∠3,则_____ ∥_____.
(2)如图,若∠1=∠2,则_____ ∥ _____ ;
若∠3=∠4,则_____ ∥ _____.
AB
DE
BC
EF
BC
AB
CD
AD
随堂检测
5.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°. 找出图中的平行线,并说明理由.
解:OA∥BC,OB∥AC.
理由如下:
∵∠1=50°,∠2=50°,
∴∠1=∠2. ∴OB∥AC
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°.
∴OA∥BC.
随堂检测
2. 平行线的判定:
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补两直线平行.
课堂小结
1. 两条直线被第三条直线所截,会产生同位角、内错角、同旁内角. 角的关系决定了两条直线是否平行,因此在做题时要掌握好“三线八角”;
