2021-2022学年人教版数学七年级下册6.1.1算术平方根课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册6.1.1算术平方根课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 449.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 13:28:13 | ||
图片预览






文档简介
(共16张PPT)
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
致亲爱的同学们
在学校的艺术节上,要举办一次美术作品展,小红同学想裁一块面积为25平方分米的正方形画布,画上自己的得意之作参加比赛,这块画布的边长应取多少分米呢?为什么?
一个正方形的面积是9,它的边长是多少?
一个正方形的面积是16,它的边长是多少?
一个正方形的面积是30,它的边长是多少?
创设情景
算术平方根
1.知识与能力:了解算术平方根的概念,理解正数的算术平方根并会用根号表示;并了解算术平方根的非负性。
2.过程与方法:会用平方运算求非负数的算术平方根。
3.情感态度与价值观:让学生体验数学与生活的密切联系,激发学生的学习兴趣。
学习目标
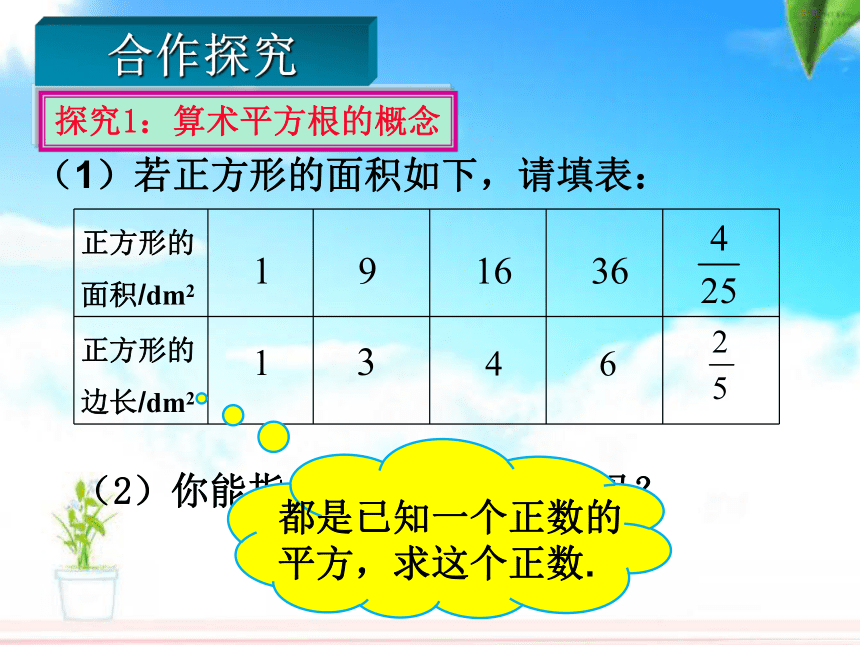
(1)若正方形的面积如下,请填表:
(2)你能指出它们的共同特点吗?
正方形的面积/dm2 1 9 16 36
正方形的边长/dm2
都是已知一个正数的平方,求这个正数.
探究1:算术平方根的概念
合作探究
一般地,如果一个正数 的平方等于 ,即 ,那么这个正数 叫做 的算术平方根. 的算术平方根记为 ,读作 “根号 , 叫做被开方数.
规定:0的算术平方根是0 ,也就是说,若 ,则 .
例如,由于 ,5是25的算术平方根,
即 .
算术平方根的概念
探究2: 求一个非负数的算术平方根
从例题的解答中可以看出:
被开方数与它对应的算术平方根有什么关系?
例1 求下列各数的算术平方根:
被开方数越大,对应的算术平方根也越大.这个结论对所有正数都成立.
解:(1)因为102=100, 所以100的算术平方根是10.
即
思考:负数有没有算术平方根?为什么?
算术平方根中被开方数的取值范围是多少?
探究3: 算术平方根的性质
由于任何数的平方都不可能是负数,所以负数没有平方根,在式子 中,被开方数 的取值范围是 ,即只有正数和0才有算术平方根。
根据算术平方根的意义可知: 具有非负性,即 。
a
≥
0
算术平方根的双重非负性.
0
≥
}
练一练
1.说出下列各式的意义,并求出它们的值:
(1) ; (2) ;
(3) ; (4) .
2.下列各式中哪些有意义?哪些无意义?为什么?
, ,
无意义
练一练
3.判断下列说法是否正确,并说明理由:
(1)25的算术平方根是5;
(2)2是 的算术平方根;
(3)-1是1的算术平方根;
(4)任意一个有理数都有算术平方根.
练一练
达标测评
1. 0.25的算术平方根是 ; 是9的算术平方根;0 的算术平方根是 .
0.5
3
0
2.若4a+1的算术平方根是5,则a 的算术平方根是______.
6
3. 的算术平方根等于______
3
9
9
归纳小结:
算术平方根
概念
表示
性质
应用
计算
(必做题):
1.求下列各数的算术平方根.
121, , , .
2.求下列各式的值.
, , .
3.3x-4为25的算术平方根,求x的值.
4.已知9的算术平方根为a,b的绝对值为4,求a-b的值.
分层作业 提高能力
(选做题):
5.已知2a-1的算术平方根是3,3a+b-1的算术平方根是4,求a、b的值.
6.若 与 互为相反数,求xy的算术平方根.
分层作业 提高能力
谢谢大家!
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
致亲爱的同学们
在学校的艺术节上,要举办一次美术作品展,小红同学想裁一块面积为25平方分米的正方形画布,画上自己的得意之作参加比赛,这块画布的边长应取多少分米呢?为什么?
一个正方形的面积是9,它的边长是多少?
一个正方形的面积是16,它的边长是多少?
一个正方形的面积是30,它的边长是多少?
创设情景
算术平方根
1.知识与能力:了解算术平方根的概念,理解正数的算术平方根并会用根号表示;并了解算术平方根的非负性。
2.过程与方法:会用平方运算求非负数的算术平方根。
3.情感态度与价值观:让学生体验数学与生活的密切联系,激发学生的学习兴趣。
学习目标
(1)若正方形的面积如下,请填表:
(2)你能指出它们的共同特点吗?
正方形的面积/dm2 1 9 16 36
正方形的边长/dm2
都是已知一个正数的平方,求这个正数.
探究1:算术平方根的概念
合作探究
一般地,如果一个正数 的平方等于 ,即 ,那么这个正数 叫做 的算术平方根. 的算术平方根记为 ,读作 “根号 , 叫做被开方数.
规定:0的算术平方根是0 ,也就是说,若 ,则 .
例如,由于 ,5是25的算术平方根,
即 .
算术平方根的概念
探究2: 求一个非负数的算术平方根
从例题的解答中可以看出:
被开方数与它对应的算术平方根有什么关系?
例1 求下列各数的算术平方根:
被开方数越大,对应的算术平方根也越大.这个结论对所有正数都成立.
解:(1)因为102=100, 所以100的算术平方根是10.
即
思考:负数有没有算术平方根?为什么?
算术平方根中被开方数的取值范围是多少?
探究3: 算术平方根的性质
由于任何数的平方都不可能是负数,所以负数没有平方根,在式子 中,被开方数 的取值范围是 ,即只有正数和0才有算术平方根。
根据算术平方根的意义可知: 具有非负性,即 。
a
≥
0
算术平方根的双重非负性.
0
≥
}
练一练
1.说出下列各式的意义,并求出它们的值:
(1) ; (2) ;
(3) ; (4) .
2.下列各式中哪些有意义?哪些无意义?为什么?
, ,
无意义
练一练
3.判断下列说法是否正确,并说明理由:
(1)25的算术平方根是5;
(2)2是 的算术平方根;
(3)-1是1的算术平方根;
(4)任意一个有理数都有算术平方根.
练一练
达标测评
1. 0.25的算术平方根是 ; 是9的算术平方根;0 的算术平方根是 .
0.5
3
0
2.若4a+1的算术平方根是5,则a 的算术平方根是______.
6
3. 的算术平方根等于______
3
9
9
归纳小结:
算术平方根
概念
表示
性质
应用
计算
(必做题):
1.求下列各数的算术平方根.
121, , , .
2.求下列各式的值.
, , .
3.3x-4为25的算术平方根,求x的值.
4.已知9的算术平方根为a,b的绝对值为4,求a-b的值.
分层作业 提高能力
(选做题):
5.已知2a-1的算术平方根是3,3a+b-1的算术平方根是4,求a、b的值.
6.若 与 互为相反数,求xy的算术平方根.
分层作业 提高能力
谢谢大家!
