2021—2022学年人教版数学七年级下册 10.1统计调查 课件(共27张)
文档属性
| 名称 | 2021—2022学年人教版数学七年级下册 10.1统计调查 课件(共27张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 14:23:47 | ||
图片预览






文档简介
(共27张PPT)
10.1 统计调查
第十章 数据的收集、整理与描述
1.我能了解全面调查的概念及掌握全面调查的步骤;
2.我能用统计图描述数据.
3.我会判断抽样调查中的总体、个体、样本、样本容量;
4.我能了解简单随机抽样.
学程一:全面调查
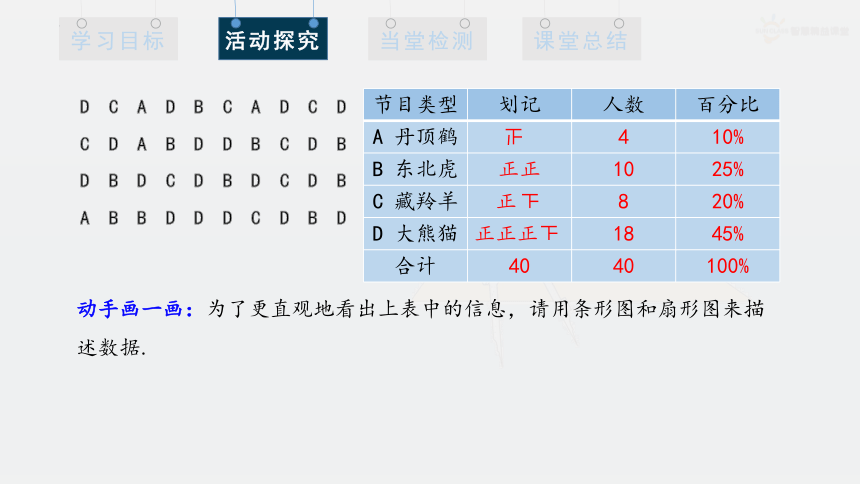
活动:如果要了解全班对丹顶鹤、东北虎、藏羚羊、大熊猫四种国家一级保护动物的喜爱情况,请同学们想一想你怎么调查.
(1):调查到什么程度就达到调查的目的了,调查的对象是什么?
(2):请你设计一张调查问卷.
调 查 问 卷 年 月 日
在以下四种国家一级保护动物中,你最喜爱的是( )(单选)
A.丹顶鹤 B.东北虎 C.藏羚羊 D.大熊猫
填完后,请将问卷交数学课代表.
(3):如果想了解男、女生喜爱动物的差异,问卷中还应该包含什么内容?
(4):假设某同学经过调查,得到以下数据,从数据中,你能看出全班同学喜爱各种动物的情况吗?怎样才能很清楚地看出全班同学喜爱各种动物的情况?
节目类型 划记 人数 百分比
A 丹顶鹤 4 10%
B 东北虎 正正 10 25%
C 藏羚羊 正 8 20%
D 大熊猫 正正正 18 45%
合计 40 40 100%
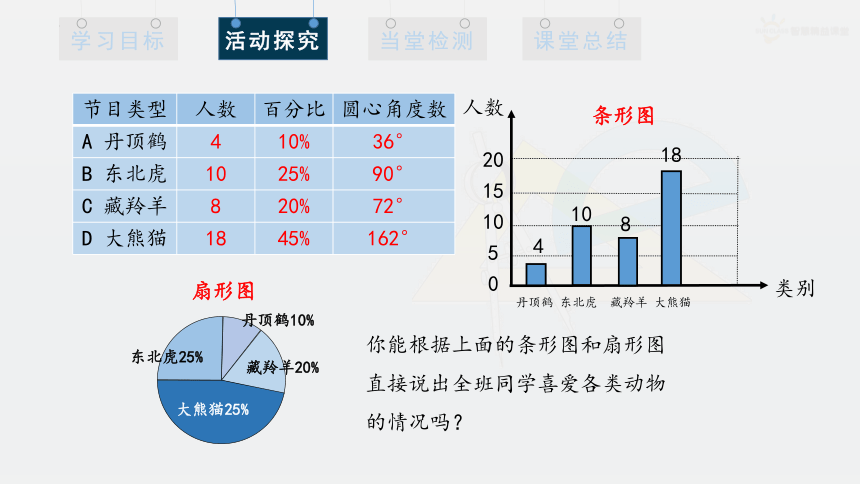
动手画一画:为了更直观地看出上表中的信息,请用条形图和扇形图来描述数据.
人数
类别
2015105 0
丹顶鹤 东北虎 藏羚羊 大熊猫
4
10
8
18
条形图
节目类型 人数 百分比 圆心角度数
A 丹顶鹤 4 10% 36°
B 东北虎 10 25% 90°
C 藏羚羊 8 20% 72°
D 大熊猫 18 45% 162°
扇形图
丹顶鹤10%
大熊猫25%
东北虎25%
藏羚羊20%
你能根据上面的条形图和扇形图直接说出全班同学喜爱各类动物的情况吗?
1.条形图能清楚地表示出每个项目的具体数目;
扇形图能清楚地表示出各部分在总体中所占的百分比.
2.统计调查的步骤:
(1)收集数据;(2)整理数据;(3)描述数据;(4)分析数据.
活动小结
像这样考察全体对象的调查叫做全面调查.
练一练
为了获得某地区中学生视力状况的数据,小明同学在调查问卷中,提出如下四个问题.其中,你认为不恰当的问题是( )
A.在你看书时,眼睛与书本的距离
B.你学习时使用的灯具
C.你是否躺着看书
D.你喜欢吃什么
D
学程二:用统计图描述数据
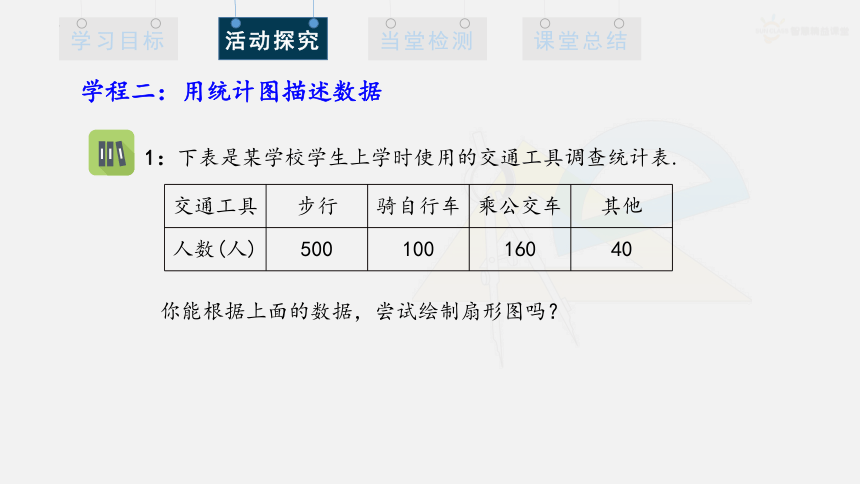
1:下表是某学校学生上学时使用的交通工具调查统计表.
你能根据上面的数据,尝试绘制扇形图吗?
交通工具 步行 骑自行车 乘公交车 其他
人数(人) 500 100 160 40
解:总人数是500+100+160+40=800(人).各部分占总体百分比如下:
步行:500÷800=62.5%,
骑自行车:100÷800=12.5%,
乘公交车:160÷800=20%,
其他:40÷800=5%.
所对应的扇形圆心角分别为
360°×62.5%=225°,360°×12.5%=45°,
360°×20%=72°,360°×5%=18°.
画出扇形图如图所示.
2:某学校在七年级随机抽取若干名学生进行“创建文明城市”知识答题,成绩分为1分,2分,3分,4分共4个等级,将调查结果绘制成如图所示的条形图和扇形图.根据图中信息,这些学生中得2分的有多少?
解:抽取的总人数为12÷30%=40(人),
得3分的人数为40×42.5%=17(人),
得2分的人数为40-3-17-12=8(人).
1.以下问题,不适合用全面调查的是( )
A.了解全班同学每周体育锻炼的时间
B.鞋厂检查生产的鞋底能承受的弯折次数
C.学校招聘教师,对应聘人员面试
D.调查全校753名学生的身高
B
2.某市30天的空气质量状况统计如下:41、107、47、100、75、92、76、93、92、129、90、78、94、77、91、103、98、127、102、105、42、109、72、105、96、112、90、123、90、149.
其中w≤50时,空气质量为优;50<w≤100时,空气质量为良;100<w≤150时,空气质量为轻微污染.
(1)根据优、良、轻微污染三种情况,用表格整理上面的数据.
(2)画出扇形图描述以上统计数据.
解:(1)如下表所示:
范围 划记 累积
优(w≤50)
良(50<w≤100)
轻微污染(100<w≤150)
3
16
11
(2)优: ,10%×360°=36°
良: ,53%×360°=191°
轻微污染: ,37%×360°=133°
优10%
良53%
轻微污染37%
学程三:抽样调查中的总体、个体、样本、样本容量
1:分别指出下列调查中的总体、个体、样本和样本容量.
(1)为调查电风扇的使用寿命,从一批电风扇中抽取20台进行测试;
(2)为调查某校七年级学生每周用于做课外作业的时间,从该校七年级中抽取50名学生进行调查.
解:(1)总体:这一批电风扇的使用寿命,
个体:每一个电风扇的使用寿命,
样本:抽出来20台电风扇的使用寿命,
样本容量:20;
(2)为调查某校七年级学生每周用于做课外作业的时间,从该校七年级中抽取50名学生进行调查.
(2)总体:该校七年级学生每周用于做课外作业的时间,
个体:每名七年级学生每周用于做课外作业的时间,
样本:抽出来50名七年级学生每周用于做课外作业的时间,
样本容量:50.
2:结合生活,下列调查采取什么调查方式更合适?
①调查本班同学的视力;
②调查一批节能灯管的使用寿命;
③为保证卫星的成功发射,对其零部件进行检查;
④对乘坐某班次客车的乘客进行安检;
⑤了解我省中学生的视力情况.
全面调查
抽样调查
全面调查
全面调查
抽样调查
适合全面调查的情况: 适合抽样调查的情况:
活动小结
调查的对象个数较少,调查容易进行
调查的结果有特别要求(如精确)
调查的对象较多
对调查对象具有破坏性
练一练
1.为了解某校八年级405名学生的体重情况,从中抽查了100名学生的体重进行统计分析,以下说法正确的是( )
A.405名学生的全体是总体 B.100名学生是总体的一个样本
C.每名学生的体重是个体 D.100名学生是样本容量
C
2.在下列考察中,是抽样调查的是( )
A.了解全校学生人数
B.调查某厂生产的黄桃罐头质量
C.调查北京市出租车数量
D.了解全班同学的家庭经济状况
B
学程四:简单随机抽样
1:观察下列情境,想一想该调查方案是否准确反映情况.
情境1:某地教育部门为了解本地区30000名中小学学生的近视情况,从中抽取了300名学生.
情境2:某市为了解全市九年级学生的体重情况,从中抽查了500名男生.
情境3:某小区为了解小区所有居民晨练的情况,从中抽查了100名老人.
不准确,情境1抽取的样本容量过小,情境2、3只调查了部分特定人群
思考
怎样做才能使得抽样调查的结果更准确呢?
如果在抽样调查时能保证每个个体都有同等的机会被选入样本,那么我们把这种抽样方法称为简单随机抽样,所得到的样本称为简单随机样本.
注意:
1.样本要具有代表性和广泛性;
2.样本容量要适当;
3.抽取的个体机会要均等.
2:为了了解今年全校学生的身高情况,小明,小华,小晨三个同学分别设计了三个方案.
小明:测量出全班每个同学的身高,以推算出全校学生的身高.
小华:在校医务室里发现了2019年全校各班的体检表,从中了解全校学生的身高情况.
小晨:在全校每个年级的二班中,抽取了学号为5的倍数的10名学生,记录他们的身高情况.
这三种做法哪一个比较好,为什么?
解:小晨的方案比较好,从全校中广泛地抽取了各年级的学生,随机地抽取部分学生,这样的调查有代表性.
1.今年某市有4万名考生参加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:
①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本;④样本容量是2000,
其中正确的有( )
A.4个 B.3个
C.2个 D.1个
C
2.为了了解学校大门出口处每天在学校放学时段的车流量,以帮助学生安全离校,有下面几个样本来统计大门出口处在学校放学时段的车流量,样本选取合适的是( )
A.抽取两天作为一个样本
B.以全年每一天为样本
C.选取每周星期日为样本
D.春、夏、秋、冬每个季节各选两周作为样本
D
3.指出下列调查运用哪种调查方式合适,并说明理由.
(1)了解全班学生中观看“汉字听写大会”这一节目的人数做的调查;
(2)了解一批药物的药效持续时间做的调查;
(3)了解全国的“甲流”疫情做的调查;
(4)了解全校初三年级学生的学习压力情况做的调查.
解:(1)适合做全面调查,理由:该调查人数较少.
(2)适合做抽样调查,理由:该调查有破坏性.
(3)适合做抽样调查,理由:该调查人数较多.
(4)适合做抽样调查,理由:该调查数目较多.
思考:全面调查和抽样调查的优、缺点是什么?
10.1 统计调查
第十章 数据的收集、整理与描述
1.我能了解全面调查的概念及掌握全面调查的步骤;
2.我能用统计图描述数据.
3.我会判断抽样调查中的总体、个体、样本、样本容量;
4.我能了解简单随机抽样.
学程一:全面调查
活动:如果要了解全班对丹顶鹤、东北虎、藏羚羊、大熊猫四种国家一级保护动物的喜爱情况,请同学们想一想你怎么调查.
(1):调查到什么程度就达到调查的目的了,调查的对象是什么?
(2):请你设计一张调查问卷.
调 查 问 卷 年 月 日
在以下四种国家一级保护动物中,你最喜爱的是( )(单选)
A.丹顶鹤 B.东北虎 C.藏羚羊 D.大熊猫
填完后,请将问卷交数学课代表.
(3):如果想了解男、女生喜爱动物的差异,问卷中还应该包含什么内容?
(4):假设某同学经过调查,得到以下数据,从数据中,你能看出全班同学喜爱各种动物的情况吗?怎样才能很清楚地看出全班同学喜爱各种动物的情况?
节目类型 划记 人数 百分比
A 丹顶鹤 4 10%
B 东北虎 正正 10 25%
C 藏羚羊 正 8 20%
D 大熊猫 正正正 18 45%
合计 40 40 100%
动手画一画:为了更直观地看出上表中的信息,请用条形图和扇形图来描述数据.
人数
类别
2015105 0
丹顶鹤 东北虎 藏羚羊 大熊猫
4
10
8
18
条形图
节目类型 人数 百分比 圆心角度数
A 丹顶鹤 4 10% 36°
B 东北虎 10 25% 90°
C 藏羚羊 8 20% 72°
D 大熊猫 18 45% 162°
扇形图
丹顶鹤10%
大熊猫25%
东北虎25%
藏羚羊20%
你能根据上面的条形图和扇形图直接说出全班同学喜爱各类动物的情况吗?
1.条形图能清楚地表示出每个项目的具体数目;
扇形图能清楚地表示出各部分在总体中所占的百分比.
2.统计调查的步骤:
(1)收集数据;(2)整理数据;(3)描述数据;(4)分析数据.
活动小结
像这样考察全体对象的调查叫做全面调查.
练一练
为了获得某地区中学生视力状况的数据,小明同学在调查问卷中,提出如下四个问题.其中,你认为不恰当的问题是( )
A.在你看书时,眼睛与书本的距离
B.你学习时使用的灯具
C.你是否躺着看书
D.你喜欢吃什么
D
学程二:用统计图描述数据
1:下表是某学校学生上学时使用的交通工具调查统计表.
你能根据上面的数据,尝试绘制扇形图吗?
交通工具 步行 骑自行车 乘公交车 其他
人数(人) 500 100 160 40
解:总人数是500+100+160+40=800(人).各部分占总体百分比如下:
步行:500÷800=62.5%,
骑自行车:100÷800=12.5%,
乘公交车:160÷800=20%,
其他:40÷800=5%.
所对应的扇形圆心角分别为
360°×62.5%=225°,360°×12.5%=45°,
360°×20%=72°,360°×5%=18°.
画出扇形图如图所示.
2:某学校在七年级随机抽取若干名学生进行“创建文明城市”知识答题,成绩分为1分,2分,3分,4分共4个等级,将调查结果绘制成如图所示的条形图和扇形图.根据图中信息,这些学生中得2分的有多少?
解:抽取的总人数为12÷30%=40(人),
得3分的人数为40×42.5%=17(人),
得2分的人数为40-3-17-12=8(人).
1.以下问题,不适合用全面调查的是( )
A.了解全班同学每周体育锻炼的时间
B.鞋厂检查生产的鞋底能承受的弯折次数
C.学校招聘教师,对应聘人员面试
D.调查全校753名学生的身高
B
2.某市30天的空气质量状况统计如下:41、107、47、100、75、92、76、93、92、129、90、78、94、77、91、103、98、127、102、105、42、109、72、105、96、112、90、123、90、149.
其中w≤50时,空气质量为优;50<w≤100时,空气质量为良;100<w≤150时,空气质量为轻微污染.
(1)根据优、良、轻微污染三种情况,用表格整理上面的数据.
(2)画出扇形图描述以上统计数据.
解:(1)如下表所示:
范围 划记 累积
优(w≤50)
良(50<w≤100)
轻微污染(100<w≤150)
3
16
11
(2)优: ,10%×360°=36°
良: ,53%×360°=191°
轻微污染: ,37%×360°=133°
优10%
良53%
轻微污染37%
学程三:抽样调查中的总体、个体、样本、样本容量
1:分别指出下列调查中的总体、个体、样本和样本容量.
(1)为调查电风扇的使用寿命,从一批电风扇中抽取20台进行测试;
(2)为调查某校七年级学生每周用于做课外作业的时间,从该校七年级中抽取50名学生进行调查.
解:(1)总体:这一批电风扇的使用寿命,
个体:每一个电风扇的使用寿命,
样本:抽出来20台电风扇的使用寿命,
样本容量:20;
(2)为调查某校七年级学生每周用于做课外作业的时间,从该校七年级中抽取50名学生进行调查.
(2)总体:该校七年级学生每周用于做课外作业的时间,
个体:每名七年级学生每周用于做课外作业的时间,
样本:抽出来50名七年级学生每周用于做课外作业的时间,
样本容量:50.
2:结合生活,下列调查采取什么调查方式更合适?
①调查本班同学的视力;
②调查一批节能灯管的使用寿命;
③为保证卫星的成功发射,对其零部件进行检查;
④对乘坐某班次客车的乘客进行安检;
⑤了解我省中学生的视力情况.
全面调查
抽样调查
全面调查
全面调查
抽样调查
适合全面调查的情况: 适合抽样调查的情况:
活动小结
调查的对象个数较少,调查容易进行
调查的结果有特别要求(如精确)
调查的对象较多
对调查对象具有破坏性
练一练
1.为了解某校八年级405名学生的体重情况,从中抽查了100名学生的体重进行统计分析,以下说法正确的是( )
A.405名学生的全体是总体 B.100名学生是总体的一个样本
C.每名学生的体重是个体 D.100名学生是样本容量
C
2.在下列考察中,是抽样调查的是( )
A.了解全校学生人数
B.调查某厂生产的黄桃罐头质量
C.调查北京市出租车数量
D.了解全班同学的家庭经济状况
B
学程四:简单随机抽样
1:观察下列情境,想一想该调查方案是否准确反映情况.
情境1:某地教育部门为了解本地区30000名中小学学生的近视情况,从中抽取了300名学生.
情境2:某市为了解全市九年级学生的体重情况,从中抽查了500名男生.
情境3:某小区为了解小区所有居民晨练的情况,从中抽查了100名老人.
不准确,情境1抽取的样本容量过小,情境2、3只调查了部分特定人群
思考
怎样做才能使得抽样调查的结果更准确呢?
如果在抽样调查时能保证每个个体都有同等的机会被选入样本,那么我们把这种抽样方法称为简单随机抽样,所得到的样本称为简单随机样本.
注意:
1.样本要具有代表性和广泛性;
2.样本容量要适当;
3.抽取的个体机会要均等.
2:为了了解今年全校学生的身高情况,小明,小华,小晨三个同学分别设计了三个方案.
小明:测量出全班每个同学的身高,以推算出全校学生的身高.
小华:在校医务室里发现了2019年全校各班的体检表,从中了解全校学生的身高情况.
小晨:在全校每个年级的二班中,抽取了学号为5的倍数的10名学生,记录他们的身高情况.
这三种做法哪一个比较好,为什么?
解:小晨的方案比较好,从全校中广泛地抽取了各年级的学生,随机地抽取部分学生,这样的调查有代表性.
1.今年某市有4万名考生参加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法:
①这4万名考生的数学中考成绩的全体是总体;②每个考生是个体;③2000名考生是总体的一个样本;④样本容量是2000,
其中正确的有( )
A.4个 B.3个
C.2个 D.1个
C
2.为了了解学校大门出口处每天在学校放学时段的车流量,以帮助学生安全离校,有下面几个样本来统计大门出口处在学校放学时段的车流量,样本选取合适的是( )
A.抽取两天作为一个样本
B.以全年每一天为样本
C.选取每周星期日为样本
D.春、夏、秋、冬每个季节各选两周作为样本
D
3.指出下列调查运用哪种调查方式合适,并说明理由.
(1)了解全班学生中观看“汉字听写大会”这一节目的人数做的调查;
(2)了解一批药物的药效持续时间做的调查;
(3)了解全国的“甲流”疫情做的调查;
(4)了解全校初三年级学生的学习压力情况做的调查.
解:(1)适合做全面调查,理由:该调查人数较少.
(2)适合做抽样调查,理由:该调查有破坏性.
(3)适合做抽样调查,理由:该调查人数较多.
(4)适合做抽样调查,理由:该调查数目较多.
思考:全面调查和抽样调查的优、缺点是什么?
