2021--2022学年人教版八年级数学下册1.2.1正比例函数 课件(共23张PPT)
文档属性
| 名称 | 2021--2022学年人教版八年级数学下册1.2.1正比例函数 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 503.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 14:59:40 | ||
图片预览







文档简介
(共23张PPT)
19.2 一次函数
第6课时 正比例函数
R·八年级下册
推进新课
正比例函数的概念
知识点 1
下面问题中的变量可用怎样的函数表示?这些函数有什么共同点?
l=2πr
m=7.8V
(1)圆的周长l随半径r的变化而变化;
(2)铁的密度为7.8g/cm3,铁的质量m随它的体积V变化而变化;
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度h随练习本的本数n的变化而变化;
h=0.5n
T=-2t
(4)冷冻一个0℃的物体,使它每分钟下降2℃,物体的温度T随冷冻时间t的变化而变化.
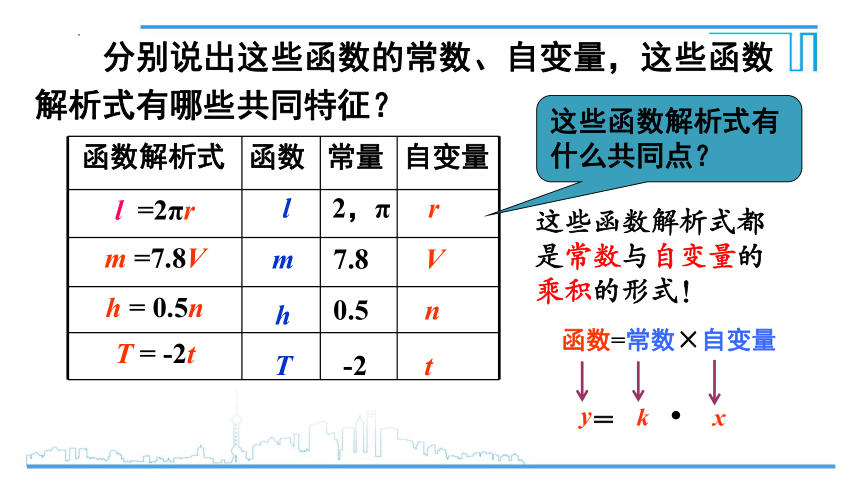
函数解析式 函数 常量 自变量
l =2πr
m =7.8V
h = 0.5n
T = -2t
这些函数解析式有什么共同点?
这些函数解析式都是常数与自变量的乘积的形式!
2,π
r
l
7.8
V
m
h
T
t
0.5
-2
n
函数=常数×自变量
y
k
x
=
分别说出这些函数的常数、自变量,这些函数解析式有哪些共同特征?
分别说出这些函数的常数、自变量,这些函数解析式有哪些共同特征?
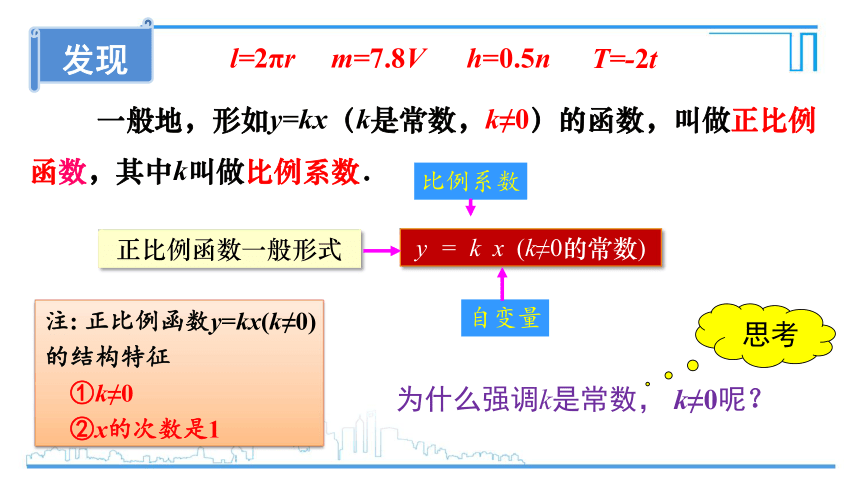
发现
发现:它们都是 的形式.
常数与自变量的乘积
一般地,形如 (k是常数,k≠0)的函数,叫做_______函数,其中k叫做__________.
y=kx
正比例
比例系数
l=2πr
m=7.8V
h=0.5n
T=-2t
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
思考
为什么强调k是常数, k≠0呢?
y = k x (k≠0的常数)
比例系数
自变量
正比例函数一般形式
注: 正比例函数y=kx(k≠0)
的结构特征
①k≠0
②x的次数是1
发现
l=2πr
m=7.8V
h=0.5n
T=-2t
1. 判断下列函数解析式是否是正比例函数?如果是,指出其比例系数是多少?
是,3
不是
是,π
不是
是,
是,
练
习
2.回答下列问题:
(1)若y=(m-1)x是正比例函数,m取值范围是 ;
(2)当n 时,y=2xn是正比例函数;
(3)当k 时,y=3x+k是正比例函数.
m≠1
=1
=0
练
习
例1 若函数y=(m-2)x|m|-1是正比例函数,求m的值.
解:由题意,得
解得m=-2.
函数是正比例函数
函数解析式可转化为y=kx
(k是常数,k ≠0)的形式.
解:(1)设正比例函数解析式是 y=kx,
把 x =-4, y =2 代入上式,得
2 = -4k,
(2)当 x=6 时, y = -3.
例2 若正比例函数的自变量 x 等于 -4 时,函数 y 的值等于2.
(1)求正比例函数的解析式;
(2)求当x=6时函数y的值.
设
代
求
写
待定系数法
例3 已知y与x+3成正比例,且当x=1时,y=-6,求y与x之间的函数关系式.
解:根据题意,可设y=k(x+3).
∵当x=1时,y=-6,
∴-6=(1+3)k,
例4 2011年开始运营的京沪高速铁路全长1318km.设列车的平均速度为300km/h.考虑以下问题:
解:乘京沪高铁列车,从始发站北京南站到终点站上海虹桥站,需要的时间大约为:
(1)乘京沪高铁列车,从始发站北京南站到终点站上海虹桥站,约需多少小时(结果保留小数点后一位)?
1318÷300≈4.4 (h)
(2)京沪高铁列车的行程 y(单位:km )与运行时间 t(单位:k )之间有何数量关系?
y=300t(0≤t≤4.4)
(3)京沪高铁列车从北京南站出发2.5h后,是否已经过了距始发站1100km的南京南站?
300×2.5=750 (km)
所以京沪高铁列车从北京南站出发2.5h后,还没经过南京南站.
因为750<1100,
1. 列式表示下列问题中的y与x的函数关系,并指出哪些是正比例函数.
(1) 正方形的边长为xcm,周长为ycm;
y=4x
正比例函数
练
习
(2) 某人一年内的月平均收入为x元,他这年(12个月)的总收入y元;
(3) 一个长方体的长为2cm,宽为1.5cm,高为xcm,体积为ycm3.
y=12x
y=3x
正比例函数
正比例函数
误 区 诊 断
错解:±2
正解:-2
误区 一
判断正比例函数时未考虑全面
当m= 时,函数y=xm -3-6m-12是正比例函数.
2
∵函数y=xm -3-6m-12是
正比例函数
2
m2-3=1,
-6m-12=0,
∴
解得m=-2
∵函数y=xm -3-6m-12是
正比例函数
2
∴m2-3=1,m=±2
错因分析:解题时忽略条件-6m-12=0.若一个函数是正比例函数,则它一定是y=kx(k是常数,k≠0)的形式.
2.下列关系中,是正比例关系的是( )
A.圆的面积S与它的半径r
B.行驶速度不变时,行驶路程s与时间t
C.正方形的面积S与边长a
D.工作总量(看作“1” )一定,工作效率w与工作时间t
随堂演练
基础巩固
1.下列函数中,y是x的正比例函数的是( )
A.y=2x-1 B.y= C.y=2x2 D.y=-2x+1
B
B
3
3. 下列说法正确的打“√”,错误的打“×”.(1)若y=kx,则y是x的正比例函数( )(2)若y=2x2,则y是x的正比例函数( )(3)若y=2(x-1)+2,则y是x的正比例函数( ) (4)若y=(2+k2)x,则y是x的正比例函数( )
×
×
√
√
(2)求当x=4时,y的值;
综合应用
4.已知:y-3与x成正比例,当x=2时,y=7.
y=2x+3
(1)求y与x之间的函数关系式;
(3)求当y=4时,x的值.
y=11
x=
5.有一块10公顷的成熟麦田,用一台收割速度为0.5公顷/时的小麦收割机来收割.
(1)求收割的面积y(单位:公顷)与收割时间x(单位:时)之间的函数关系式;
(2)求收割完这块麦田需用的时间.
解:(1)y=0.5x;
(2)把y=10代入y=0.5x中,得10=0.5x.
解得x=20,即收割完这块麦田需要20小时.
课堂小结
正比例函数
2.表达式:y=kx (k是常数,k≠0).
1.定义:一般地,形如 (k是常数,k≠0)的函数,叫做_______函数,其中k叫做_________.
y=kx
正比例
比例系数
正比例函数的概念
形式:y=kx(k≠0)
求正比例函数的解析式
利用正比例函数解决简单的实际问题
19.2 一次函数
第6课时 正比例函数
R·八年级下册
推进新课
正比例函数的概念
知识点 1
下面问题中的变量可用怎样的函数表示?这些函数有什么共同点?
l=2πr
m=7.8V
(1)圆的周长l随半径r的变化而变化;
(2)铁的密度为7.8g/cm3,铁的质量m随它的体积V变化而变化;
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度h随练习本的本数n的变化而变化;
h=0.5n
T=-2t
(4)冷冻一个0℃的物体,使它每分钟下降2℃,物体的温度T随冷冻时间t的变化而变化.
函数解析式 函数 常量 自变量
l =2πr
m =7.8V
h = 0.5n
T = -2t
这些函数解析式有什么共同点?
这些函数解析式都是常数与自变量的乘积的形式!
2,π
r
l
7.8
V
m
h
T
t
0.5
-2
n
函数=常数×自变量
y
k
x
=
分别说出这些函数的常数、自变量,这些函数解析式有哪些共同特征?
分别说出这些函数的常数、自变量,这些函数解析式有哪些共同特征?
发现
发现:它们都是 的形式.
常数与自变量的乘积
一般地,形如 (k是常数,k≠0)的函数,叫做_______函数,其中k叫做__________.
y=kx
正比例
比例系数
l=2πr
m=7.8V
h=0.5n
T=-2t
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
思考
为什么强调k是常数, k≠0呢?
y = k x (k≠0的常数)
比例系数
自变量
正比例函数一般形式
注: 正比例函数y=kx(k≠0)
的结构特征
①k≠0
②x的次数是1
发现
l=2πr
m=7.8V
h=0.5n
T=-2t
1. 判断下列函数解析式是否是正比例函数?如果是,指出其比例系数是多少?
是,3
不是
是,π
不是
是,
是,
练
习
2.回答下列问题:
(1)若y=(m-1)x是正比例函数,m取值范围是 ;
(2)当n 时,y=2xn是正比例函数;
(3)当k 时,y=3x+k是正比例函数.
m≠1
=1
=0
练
习
例1 若函数y=(m-2)x|m|-1是正比例函数,求m的值.
解:由题意,得
解得m=-2.
函数是正比例函数
函数解析式可转化为y=kx
(k是常数,k ≠0)的形式.
解:(1)设正比例函数解析式是 y=kx,
把 x =-4, y =2 代入上式,得
2 = -4k,
(2)当 x=6 时, y = -3.
例2 若正比例函数的自变量 x 等于 -4 时,函数 y 的值等于2.
(1)求正比例函数的解析式;
(2)求当x=6时函数y的值.
设
代
求
写
待定系数法
例3 已知y与x+3成正比例,且当x=1时,y=-6,求y与x之间的函数关系式.
解:根据题意,可设y=k(x+3).
∵当x=1时,y=-6,
∴-6=(1+3)k,
例4 2011年开始运营的京沪高速铁路全长1318km.设列车的平均速度为300km/h.考虑以下问题:
解:乘京沪高铁列车,从始发站北京南站到终点站上海虹桥站,需要的时间大约为:
(1)乘京沪高铁列车,从始发站北京南站到终点站上海虹桥站,约需多少小时(结果保留小数点后一位)?
1318÷300≈4.4 (h)
(2)京沪高铁列车的行程 y(单位:km )与运行时间 t(单位:k )之间有何数量关系?
y=300t(0≤t≤4.4)
(3)京沪高铁列车从北京南站出发2.5h后,是否已经过了距始发站1100km的南京南站?
300×2.5=750 (km)
所以京沪高铁列车从北京南站出发2.5h后,还没经过南京南站.
因为750<1100,
1. 列式表示下列问题中的y与x的函数关系,并指出哪些是正比例函数.
(1) 正方形的边长为xcm,周长为ycm;
y=4x
正比例函数
练
习
(2) 某人一年内的月平均收入为x元,他这年(12个月)的总收入y元;
(3) 一个长方体的长为2cm,宽为1.5cm,高为xcm,体积为ycm3.
y=12x
y=3x
正比例函数
正比例函数
误 区 诊 断
错解:±2
正解:-2
误区 一
判断正比例函数时未考虑全面
当m= 时,函数y=xm -3-6m-12是正比例函数.
2
∵函数y=xm -3-6m-12是
正比例函数
2
m2-3=1,
-6m-12=0,
∴
解得m=-2
∵函数y=xm -3-6m-12是
正比例函数
2
∴m2-3=1,m=±2
错因分析:解题时忽略条件-6m-12=0.若一个函数是正比例函数,则它一定是y=kx(k是常数,k≠0)的形式.
2.下列关系中,是正比例关系的是( )
A.圆的面积S与它的半径r
B.行驶速度不变时,行驶路程s与时间t
C.正方形的面积S与边长a
D.工作总量(看作“1” )一定,工作效率w与工作时间t
随堂演练
基础巩固
1.下列函数中,y是x的正比例函数的是( )
A.y=2x-1 B.y= C.y=2x2 D.y=-2x+1
B
B
3
3. 下列说法正确的打“√”,错误的打“×”.(1)若y=kx,则y是x的正比例函数( )(2)若y=2x2,则y是x的正比例函数( )(3)若y=2(x-1)+2,则y是x的正比例函数( ) (4)若y=(2+k2)x,则y是x的正比例函数( )
×
×
√
√
(2)求当x=4时,y的值;
综合应用
4.已知:y-3与x成正比例,当x=2时,y=7.
y=2x+3
(1)求y与x之间的函数关系式;
(3)求当y=4时,x的值.
y=11
x=
5.有一块10公顷的成熟麦田,用一台收割速度为0.5公顷/时的小麦收割机来收割.
(1)求收割的面积y(单位:公顷)与收割时间x(单位:时)之间的函数关系式;
(2)求收割完这块麦田需用的时间.
解:(1)y=0.5x;
(2)把y=10代入y=0.5x中,得10=0.5x.
解得x=20,即收割完这块麦田需要20小时.
课堂小结
正比例函数
2.表达式:y=kx (k是常数,k≠0).
1.定义:一般地,形如 (k是常数,k≠0)的函数,叫做_______函数,其中k叫做_________.
y=kx
正比例
比例系数
正比例函数的概念
形式:y=kx(k≠0)
求正比例函数的解析式
利用正比例函数解决简单的实际问题
