2021—2022学年沪科版数学八年级下册20.2.2数据的离散程度 课件(共18张PPT)
文档属性
| 名称 | 2021—2022学年沪科版数学八年级下册20.2.2数据的离散程度 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 561.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
20.2.2 数据的离散程度
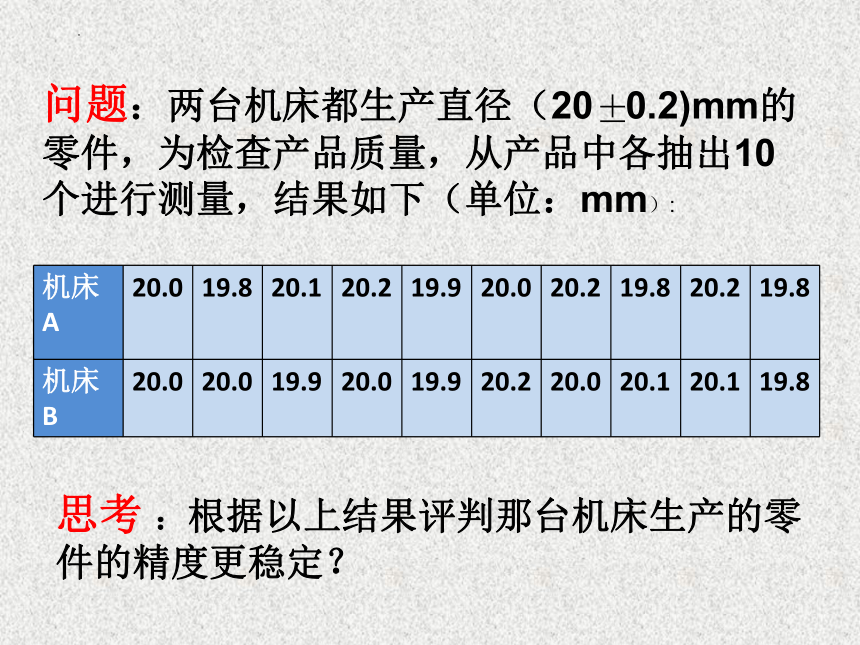
问题:两台机床都生产直径(20 0.2)mm的零件,为检查产品质量,从产品中各抽出10个进行测量,结果如下(单位:mm):
机床A 20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.8 20.2 19.8
机床B 20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
思考 :根据以上结果评判那台机床生产的零件的精度更稳定?
中位数:A组数据的中位数是20.0
B组数据的中位数是20.0
数据的离散程度:???
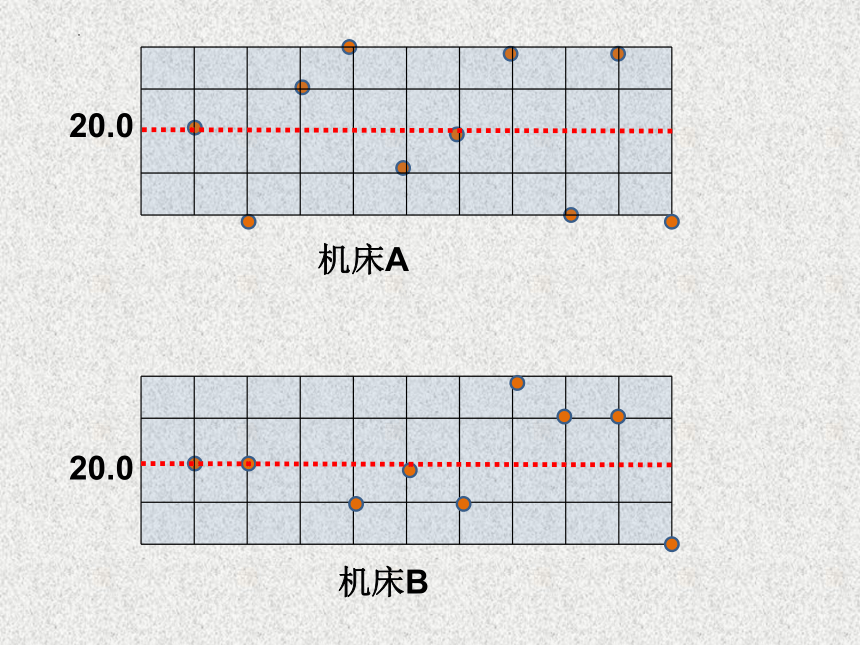
20.0
20.0
机床A
机床B
甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
2月21日 2月22日 2月24日 2月25日 2月26日 2月27日 2月28日
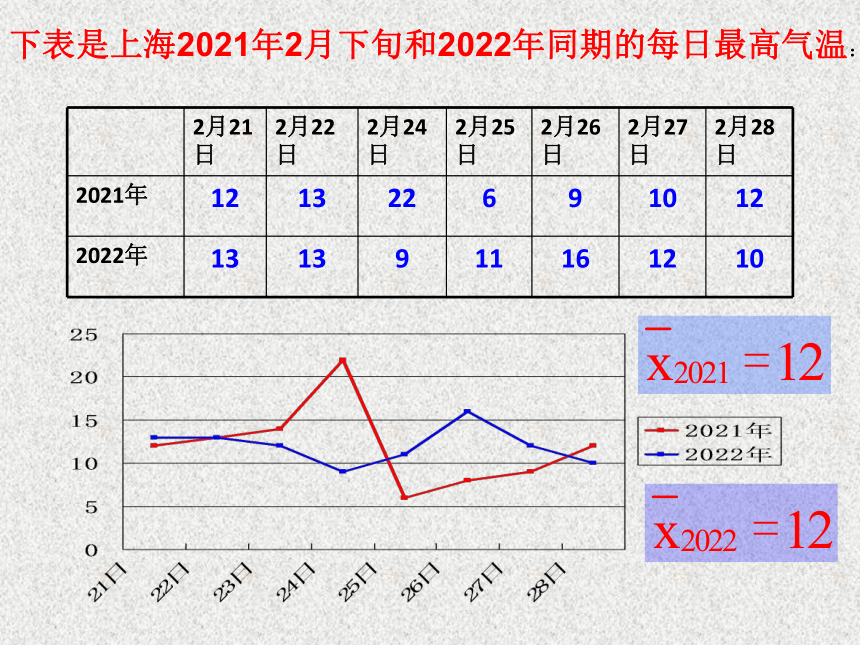
2021年 12 13 22 6 9 10 12
2022年 13 13 9 11 16 12 10
下表是上海2021年2月下旬和2022年同期的每日最高气温:
方差越小,这组数据的离散程度越小,数据就越集中,也就越稳定。
在一组数据中,我们用各数据与它们的平均数的差的平方的平均数来衡量这组数据的离散程度,并把它叫做这组数据的方差(variance ) ,通常用S2 表示,即
问题:两台机床都生产直径(20 0.2)mm的零件,为检查产品质量,从产品中各抽出10个进行测量,结果如下(单位:mm):
机床A 20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.8 20.2 19.8
机床B 20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
由于0.026>0.012,可知机床A生产的10个零件直径比机床B生产的10个零件直径波动要大机床B生产的零件的精度更稳定。
甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
想一想 通过以上练习你有什么发现吗?
一般地,在平均数相同的情况下,方差越大,则意味着这组数据对平均数的离散程度也越大,也就越不稳定。
在两组 数据的平均数相差较大时,以及在比较单位不相同时,不能直接用方差来比较它们的离散程度。
例1某足球队对运动员进行射点球成绩测试,每人每天射点球5次,在10天中,运动员大刚的进球个数分别是:
5 4 5 3 3 5 2 5 3 5
(1)求大刚进球个数的平均数;
(2)求大刚进球个数的方差.
解:(1)大刚进球个数的平均数为
(2)大刚进球个数的方差为
10
5
3
5
2
5
3
3
5
4
5
+
+
+
+
+
+
+
+
+
=
x
=4(个);
10
)
4
5
(
)
4
5
(
)
4
4
(
)
4
5
(
2
2
2
2
2
-
+
+
-
+
-
+
-
=
L
s
=1.2
例题讲解
小林
1.小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中,新手是___
课堂练习
2.某学生在一学年的6次测验中,语文、数学成绩分别为(单位:分):
语文:80,84,88,76,79,85;
数学:80,75,90,64,88,95.
试估计该学生是数学成绩稳定还是语文成绩稳定?
解:
1 2 3 4 5
甲 52 50 51 49 53
乙 51 51 51 48 54
3.有甲、乙两种新品种的水稻,在进行杂交配系时要选取产量较高、稳定性较好的一种,种植后各抽取5块田获取数据,每亩产量分别如下表:(单位:kg)
(1)哪一品种平均亩产较高?
(2)哪一品种稳定性较好?
(3)据统计,应选哪一品种做杂交配系?
解 (1)x甲=51,x乙=51,∴甲、乙平均亩产 同
(2)s甲2=2,s乙2=3.6,
∵s甲2<s乙2,
∴甲品 种稳定性好
(3)应选择甲品种做杂交配系
x
(x1- )
x
(x2- )
x
(x3- )
……
x
(xn- )
2
2
2
2
+
+
+
+
[
]
n
1
S2=
在一组数据中,各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差,通常用S2 表示,即
方差越小,这组数据的离散程度越小,数据就越集中,平均数代表性就越大.
课堂小结
20.2.2 数据的离散程度
问题:两台机床都生产直径(20 0.2)mm的零件,为检查产品质量,从产品中各抽出10个进行测量,结果如下(单位:mm):
机床A 20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.8 20.2 19.8
机床B 20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
思考 :根据以上结果评判那台机床生产的零件的精度更稳定?
中位数:A组数据的中位数是20.0
B组数据的中位数是20.0
数据的离散程度:???
20.0
20.0
机床A
机床B
甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
2月21日 2月22日 2月24日 2月25日 2月26日 2月27日 2月28日
2021年 12 13 22 6 9 10 12
2022年 13 13 9 11 16 12 10
下表是上海2021年2月下旬和2022年同期的每日最高气温:
方差越小,这组数据的离散程度越小,数据就越集中,也就越稳定。
在一组数据中,我们用各数据与它们的平均数的差的平方的平均数来衡量这组数据的离散程度,并把它叫做这组数据的方差(variance ) ,通常用S2 表示,即
问题:两台机床都生产直径(20 0.2)mm的零件,为检查产品质量,从产品中各抽出10个进行测量,结果如下(单位:mm):
机床A 20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.8 20.2 19.8
机床B 20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
由于0.026>0.012,可知机床A生产的10个零件直径比机床B生产的10个零件直径波动要大机床B生产的零件的精度更稳定。
甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
想一想 通过以上练习你有什么发现吗?
一般地,在平均数相同的情况下,方差越大,则意味着这组数据对平均数的离散程度也越大,也就越不稳定。
在两组 数据的平均数相差较大时,以及在比较单位不相同时,不能直接用方差来比较它们的离散程度。
例1某足球队对运动员进行射点球成绩测试,每人每天射点球5次,在10天中,运动员大刚的进球个数分别是:
5 4 5 3 3 5 2 5 3 5
(1)求大刚进球个数的平均数;
(2)求大刚进球个数的方差.
解:(1)大刚进球个数的平均数为
(2)大刚进球个数的方差为
10
5
3
5
2
5
3
3
5
4
5
+
+
+
+
+
+
+
+
+
=
x
=4(个);
10
)
4
5
(
)
4
5
(
)
4
4
(
)
4
5
(
2
2
2
2
2
-
+
+
-
+
-
+
-
=
L
s
=1.2
例题讲解
小林
1.小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中,新手是___
课堂练习
2.某学生在一学年的6次测验中,语文、数学成绩分别为(单位:分):
语文:80,84,88,76,79,85;
数学:80,75,90,64,88,95.
试估计该学生是数学成绩稳定还是语文成绩稳定?
解:
1 2 3 4 5
甲 52 50 51 49 53
乙 51 51 51 48 54
3.有甲、乙两种新品种的水稻,在进行杂交配系时要选取产量较高、稳定性较好的一种,种植后各抽取5块田获取数据,每亩产量分别如下表:(单位:kg)
(1)哪一品种平均亩产较高?
(2)哪一品种稳定性较好?
(3)据统计,应选哪一品种做杂交配系?
解 (1)x甲=51,x乙=51,∴甲、乙平均亩产 同
(2)s甲2=2,s乙2=3.6,
∵s甲2<s乙2,
∴甲品 种稳定性好
(3)应选择甲品种做杂交配系
x
(x1- )
x
(x2- )
x
(x3- )
……
x
(xn- )
2
2
2
2
+
+
+
+
[
]
n
1
S2=
在一组数据中,各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差,通常用S2 表示,即
方差越小,这组数据的离散程度越小,数据就越集中,平均数代表性就越大.
课堂小结
