2021-2022学年北师大版数学七年级下册第二章相交线与平行线 复习课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年北师大版数学七年级下册第二章相交线与平行线 复习课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 398.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 15:19:18 | ||
图片预览




文档简介
(共25张PPT)
第二章
相交线与平行线
(复习)
a
b
平 行
O
相交
a
b
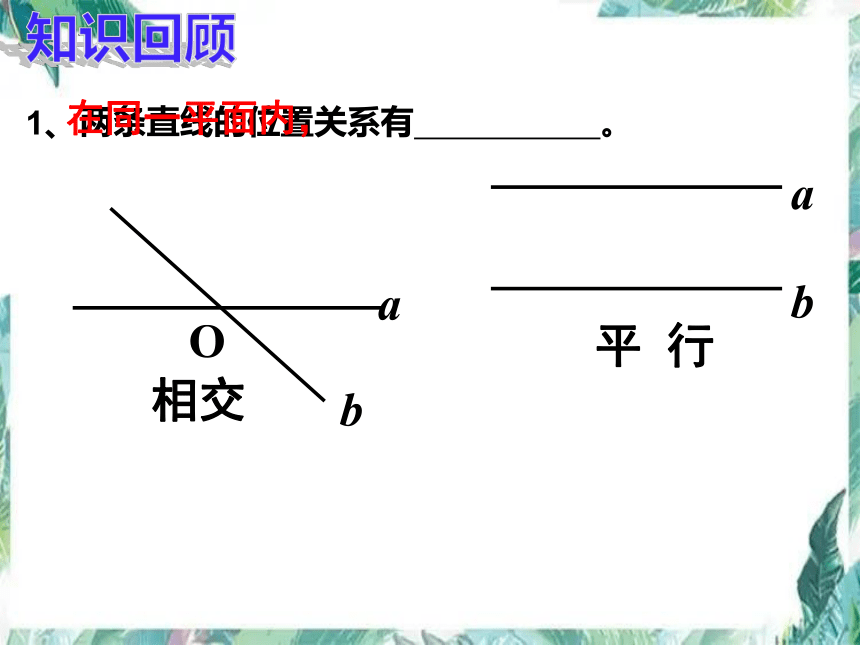
两条直线的位置关系有 。
1、
在同一平面内,
知识回顾
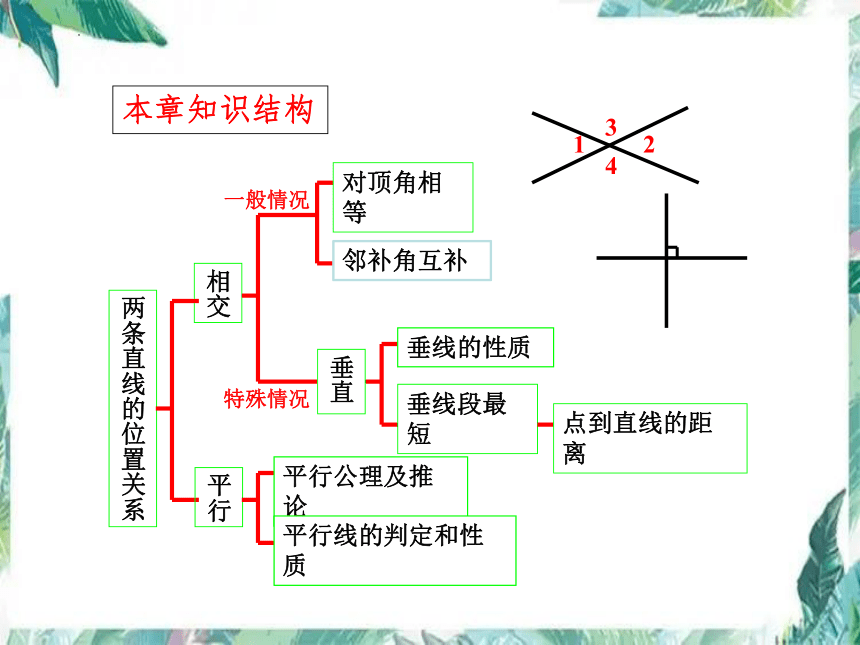
相交
一般情况
特殊情况
对顶角相等
邻补角互补
垂直
垂线段最短
点到直线的距离
1
2
3
4
垂线的性质
本章知识结构
两条直线的位置关系
平行
平行公理及推论
平行线的判定和性质
1.余角与补角
(1)定义:如果两个角的和是________,那么称这两个角互为余角;如果两个角的和是_________,那么称这两个角互为补角.
(2)性质:同角或等角的余角__________,同角或等角的补角__________.
2.对顶角
(1)定义:两个角有公共顶点,且它们的两边互为_______________,这样的两个角叫做对顶角.
(2)性质:对顶角__________.
第二章 | 复习
知识归纳
相等
90°
180°
相等
反向延长线
相等
数学·北师版(BS)
余角、补角
1、已知一个角为50度,则它的余角为 度,补角为 度。
40
130
2、 如图,在电线杆C点处引两根拉线固定电线杆,若∠1+∠2=90°,∠2+∠3=90°,那么∠1___∠3 (填 >, =, < )
理由是____________________。
=
同角的余角相等
2
1
3
C
新课标(BS)
48°
知识点一 余角、补角、对顶角
要注意挖掘题目中的隐含条件——对顶角
解题策略:隐含条件——对顶角。
例题巩固
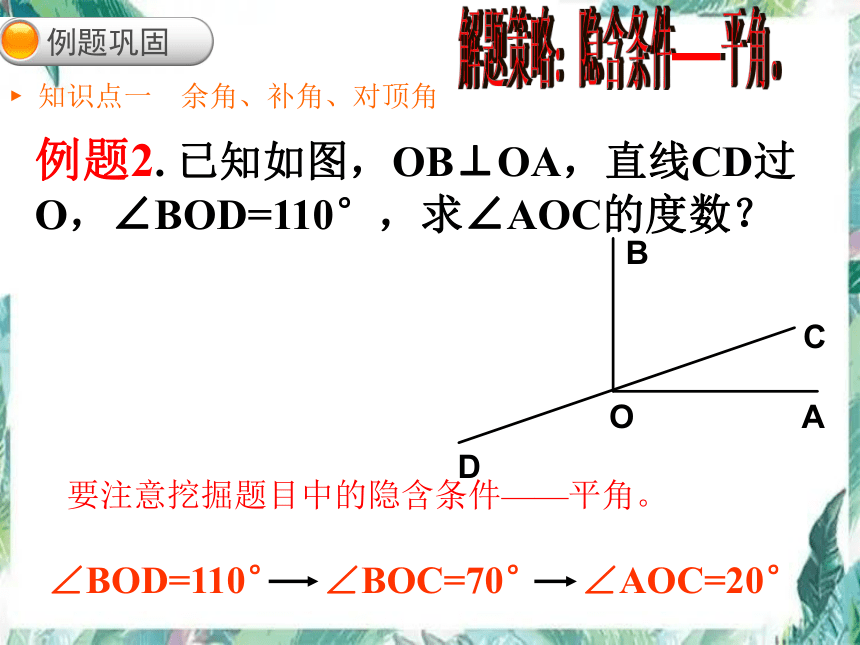
例题2. 已知如图,OB⊥OA,直线CD过O,∠BOD=110°,求∠AOC的度数?
∠BOD=110° ∠BOC=70° ∠AOC=20°
知识点一 余角、补角、对顶角
要注意挖掘题目中的隐含条件——平角。
例题巩固
解题策略:隐含条件——平角。
达 标
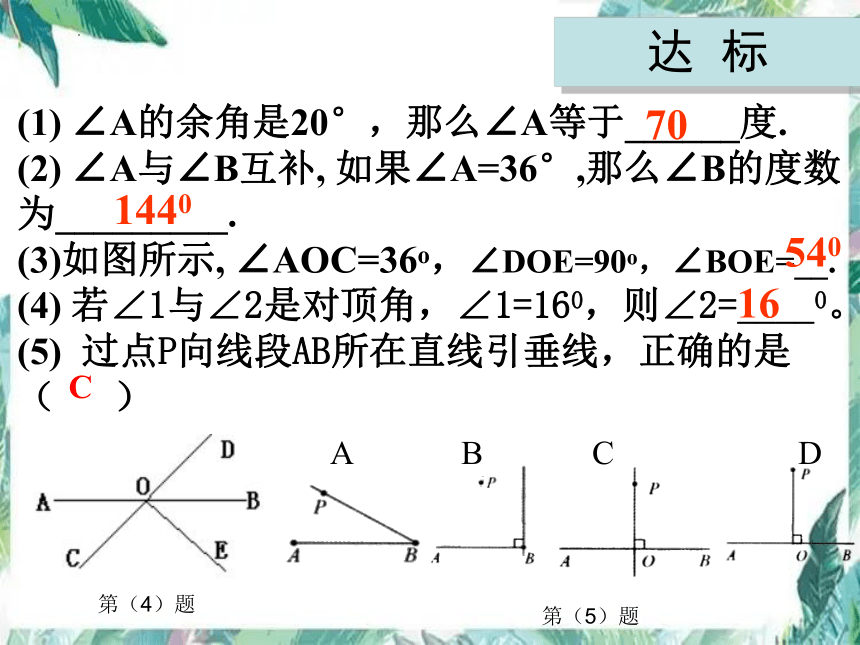
(1) ∠A的余角是20°,那么∠A等于______度.
(2) ∠A与∠B互补, 如果∠A=36°,那么∠B的度数为_________.
(3)如图所示, ∠AOC=36o,∠DOE=90o,∠BOE=__.
(4) 若∠1与∠2是对顶角,∠1=160,则∠2=____0。(5) 过点P向线段AB所在直线引垂线,正确的是( )
70
1440
540
16
A B C D
第(4)题
第(5)题
C
A
B
C
D
E
F
H
G
A
B
C
D
E
F
H
G
A
B
C
D
E
F
H
G
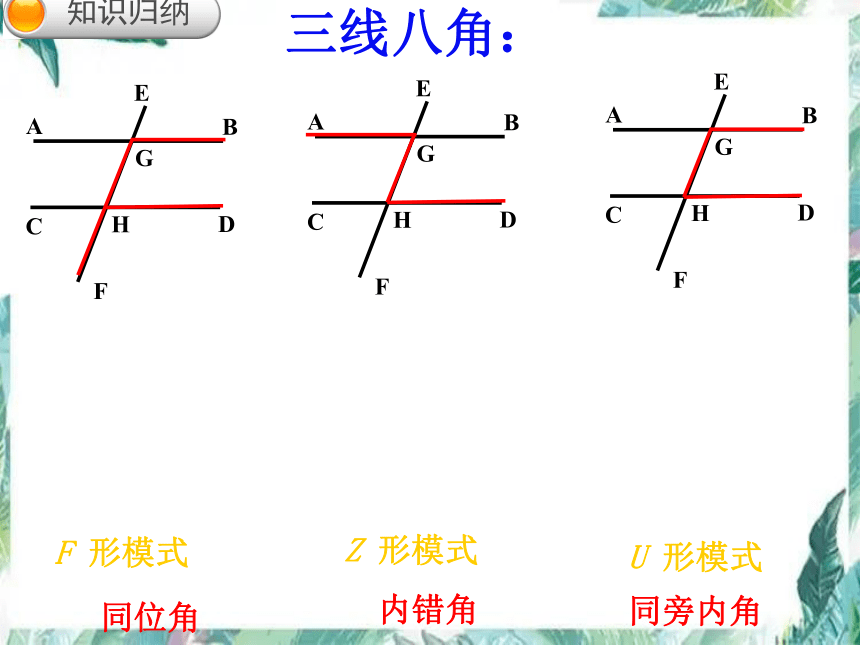
F 形模式
Z 形模式
U 形模式
同位角
内错角
同旁内角
三线八角:
知识归纳
两直线被第三条直线所截,则( )
A、同位角相等 B、内错角相等
C、同旁内角互补D、以上都不对
平行线的判定
两直线平行
条件
结论
同位角相等
内错角相等
同旁内角互补
条件
同位角相等
内错角相等
同旁内角互补
结论
两直线平行
平
行
线
的
性
质
同一平面内,平行于同一条直线的两条直
线互相平行
角的关系
直线平行
判定
确定其它角
的关系
性质
知识归纳
知识点二 平行的判定
如图2-2所示,要使AE∥BC,需要添加一个什么条件?有几种添加方法?
图2-2
解:添加∠DAE=∠ABC,
可得AE∥BC(同位角相等,两直线平行);
添加∠EAC=∠ACB,
可得AE∥BC(内错角相等,两直线平行);
添加∠BAE+∠ABC=180°,
可得AE∥BC(同旁内角互补,两直线平行).
所以有三种添加方法:∠DAE=∠ABC,∠EAC=∠ACB,∠BAE+∠ABC=180°.
[易错警示]能够准确判断同位角、内错角、同旁内角等各种位置关系。
数学·北师版(BS)
例题3已知,如图直线AB、CD被直线EF所截,且∠1+∠2=180°
求证:AB//CD (在括号中填写下列理由)
A
B
C
D
E
F
1
2
H
G
证明:
∵∠1+∠3=180°( )
∠1+∠2=180°( )
3
∴ ∠3=∠2 ( )
∴AB//CD( )
平角的定义
已知
同角的补角相等
同位角相等,两直线平行
方法唯一吗?
要注意挖掘题目中的隐含条件——平角,对顶角等
例题巩固
.
(1)如图已知∠3=120°
,则∠5=( )
A 30° B 60°
C 120° D 不确定
(2)如图已知∠1=∠2,
∠3=120°,则∠5=( )
A 30° B 60°
C 120° D 不确定
A
B
C
D
3
2
5
4
1
角的关系
直线平行
判定
确定其它角
的关系
性质
解题策略:利用平行线去转化。
知识点三 平行的性质
达 标
D
C
D
E
C
A
B
例4、 如图,AB//CD, ∠B=∠D, 那么,BC与DE平行吗?为什么?
解: BC // DE
理由:∵ AB // CD ( )
∴∠B = ( ) ( )
∵∠B = ∠D ( )
∴( )=∠D ( )
∴ BC // DE ( )
已知
∠C
两直线平行 ,内错角相等
已知
∠C
等量代换
内错角相等,两直线平行
解题策略:找一个关联角
(等量代换)
例题巩固
(1)、如图,∠1=∠2,∠C=∠D,那么∠A=∠F,为什么?
达 标
证明:∵ ∠1=∠2(已知)
∠2=∠3( 对顶角相等 )
∴∠1=∠3( 等量代换 )
∴EC∥DB(同位角相等,两直线平行)
∴ ∠4 =∠C(两直线平行,同位角相等)
又∵ ∠C=∠D(已知)
∴ ∠4 =∠D(等量代换)
∴ DF∥AC(同位角相等,两直线平行)
∴ ∠A =∠F(两直线平行,内错角相等)
灵活应用平行的条件
和性质
达 标
(1)、如图,∠1=∠2,∠C=∠D,那么∠A=∠F,为什么?
达 标
原题稍加变化后得到下题:
准确书写:
作平行线或作垂线:过…作…
E
过P点作PE∥AB
一题多解
求证:AB\\CD时,∠A+∠APC+∠A=360°
解题策略:添加辅助线去转化。
你的思维超乎你想象
添加辅助线的方法:
①添加平行线
②构造三角形
连结线段
作延长线
解题策略:添加辅助线。
强 化
4.已知:AB∥CD。试探索
①∠A、∠C与∠AEC之间的关系;
②∠B、∠D与∠BFD之间的关系.
A
B
C
D
E
F
相交线与平行线
相交线
平行线
补角、余角、对顶角
丰富情景
探索直线平行的特征
探索直线平行的条件
同位角
内错角
同旁内角
梳理一下
请你谈一谈本节
复习课的收获?
平行线与相交线
角的关系
直线平行
判定
确定其它角
的关系
性质
解题策略:1、隐含条件
2、利用平行线去转化
3、找一个关联角(等量代换)
4、添加辅助线
谢谢!
第二章
相交线与平行线
(复习)
a
b
平 行
O
相交
a
b
两条直线的位置关系有 。
1、
在同一平面内,
知识回顾
相交
一般情况
特殊情况
对顶角相等
邻补角互补
垂直
垂线段最短
点到直线的距离
1
2
3
4
垂线的性质
本章知识结构
两条直线的位置关系
平行
平行公理及推论
平行线的判定和性质
1.余角与补角
(1)定义:如果两个角的和是________,那么称这两个角互为余角;如果两个角的和是_________,那么称这两个角互为补角.
(2)性质:同角或等角的余角__________,同角或等角的补角__________.
2.对顶角
(1)定义:两个角有公共顶点,且它们的两边互为_______________,这样的两个角叫做对顶角.
(2)性质:对顶角__________.
第二章 | 复习
知识归纳
相等
90°
180°
相等
反向延长线
相等
数学·北师版(BS)
余角、补角
1、已知一个角为50度,则它的余角为 度,补角为 度。
40
130
2、 如图,在电线杆C点处引两根拉线固定电线杆,若∠1+∠2=90°,∠2+∠3=90°,那么∠1___∠3 (填 >, =, < )
理由是____________________。
=
同角的余角相等
2
1
3
C
新课标(BS)
48°
知识点一 余角、补角、对顶角
要注意挖掘题目中的隐含条件——对顶角
解题策略:隐含条件——对顶角。
例题巩固
例题2. 已知如图,OB⊥OA,直线CD过O,∠BOD=110°,求∠AOC的度数?
∠BOD=110° ∠BOC=70° ∠AOC=20°
知识点一 余角、补角、对顶角
要注意挖掘题目中的隐含条件——平角。
例题巩固
解题策略:隐含条件——平角。
达 标
(1) ∠A的余角是20°,那么∠A等于______度.
(2) ∠A与∠B互补, 如果∠A=36°,那么∠B的度数为_________.
(3)如图所示, ∠AOC=36o,∠DOE=90o,∠BOE=__.
(4) 若∠1与∠2是对顶角,∠1=160,则∠2=____0。(5) 过点P向线段AB所在直线引垂线,正确的是( )
70
1440
540
16
A B C D
第(4)题
第(5)题
C
A
B
C
D
E
F
H
G
A
B
C
D
E
F
H
G
A
B
C
D
E
F
H
G
F 形模式
Z 形模式
U 形模式
同位角
内错角
同旁内角
三线八角:
知识归纳
两直线被第三条直线所截,则( )
A、同位角相等 B、内错角相等
C、同旁内角互补D、以上都不对
平行线的判定
两直线平行
条件
结论
同位角相等
内错角相等
同旁内角互补
条件
同位角相等
内错角相等
同旁内角互补
结论
两直线平行
平
行
线
的
性
质
同一平面内,平行于同一条直线的两条直
线互相平行
角的关系
直线平行
判定
确定其它角
的关系
性质
知识归纳
知识点二 平行的判定
如图2-2所示,要使AE∥BC,需要添加一个什么条件?有几种添加方法?
图2-2
解:添加∠DAE=∠ABC,
可得AE∥BC(同位角相等,两直线平行);
添加∠EAC=∠ACB,
可得AE∥BC(内错角相等,两直线平行);
添加∠BAE+∠ABC=180°,
可得AE∥BC(同旁内角互补,两直线平行).
所以有三种添加方法:∠DAE=∠ABC,∠EAC=∠ACB,∠BAE+∠ABC=180°.
[易错警示]能够准确判断同位角、内错角、同旁内角等各种位置关系。
数学·北师版(BS)
例题3已知,如图直线AB、CD被直线EF所截,且∠1+∠2=180°
求证:AB//CD (在括号中填写下列理由)
A
B
C
D
E
F
1
2
H
G
证明:
∵∠1+∠3=180°( )
∠1+∠2=180°( )
3
∴ ∠3=∠2 ( )
∴AB//CD( )
平角的定义
已知
同角的补角相等
同位角相等,两直线平行
方法唯一吗?
要注意挖掘题目中的隐含条件——平角,对顶角等
例题巩固
.
(1)如图已知∠3=120°
,则∠5=( )
A 30° B 60°
C 120° D 不确定
(2)如图已知∠1=∠2,
∠3=120°,则∠5=( )
A 30° B 60°
C 120° D 不确定
A
B
C
D
3
2
5
4
1
角的关系
直线平行
判定
确定其它角
的关系
性质
解题策略:利用平行线去转化。
知识点三 平行的性质
达 标
D
C
D
E
C
A
B
例4、 如图,AB//CD, ∠B=∠D, 那么,BC与DE平行吗?为什么?
解: BC // DE
理由:∵ AB // CD ( )
∴∠B = ( ) ( )
∵∠B = ∠D ( )
∴( )=∠D ( )
∴ BC // DE ( )
已知
∠C
两直线平行 ,内错角相等
已知
∠C
等量代换
内错角相等,两直线平行
解题策略:找一个关联角
(等量代换)
例题巩固
(1)、如图,∠1=∠2,∠C=∠D,那么∠A=∠F,为什么?
达 标
证明:∵ ∠1=∠2(已知)
∠2=∠3( 对顶角相等 )
∴∠1=∠3( 等量代换 )
∴EC∥DB(同位角相等,两直线平行)
∴ ∠4 =∠C(两直线平行,同位角相等)
又∵ ∠C=∠D(已知)
∴ ∠4 =∠D(等量代换)
∴ DF∥AC(同位角相等,两直线平行)
∴ ∠A =∠F(两直线平行,内错角相等)
灵活应用平行的条件
和性质
达 标
(1)、如图,∠1=∠2,∠C=∠D,那么∠A=∠F,为什么?
达 标
原题稍加变化后得到下题:
准确书写:
作平行线或作垂线:过…作…
E
过P点作PE∥AB
一题多解
求证:AB\\CD时,∠A+∠APC+∠A=360°
解题策略:添加辅助线去转化。
你的思维超乎你想象
添加辅助线的方法:
①添加平行线
②构造三角形
连结线段
作延长线
解题策略:添加辅助线。
强 化
4.已知:AB∥CD。试探索
①∠A、∠C与∠AEC之间的关系;
②∠B、∠D与∠BFD之间的关系.
A
B
C
D
E
F
相交线与平行线
相交线
平行线
补角、余角、对顶角
丰富情景
探索直线平行的特征
探索直线平行的条件
同位角
内错角
同旁内角
梳理一下
请你谈一谈本节
复习课的收获?
平行线与相交线
角的关系
直线平行
判定
确定其它角
的关系
性质
解题策略:1、隐含条件
2、利用平行线去转化
3、找一个关联角(等量代换)
4、添加辅助线
谢谢!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
