2021--2022学年北师大版七年级数学下册第五章生活中的轴对称 复习课课件(共22张PPT)
文档属性
| 名称 | 2021--2022学年北师大版七年级数学下册第五章生活中的轴对称 复习课课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 952.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 15:33:58 | ||
图片预览




文档简介
(共22张PPT)
北师大版七年级数学下册
第五章 生活中的轴对称
复习题
一、基础过关
典型例题分析
例1. (1)等腰三角形的一个角是80°,则它的底角 °
80或50
变式1:如果等腰三角形的两个内角的度数之比为1∶4,那么这个三角形的底角
是 °;
变式2:已知等腰三角形一腰上的高与另一
腰的夹角为45°,求其顶角度数为 ;
变式训练
°
80或30
45或135
中垂线典型例题
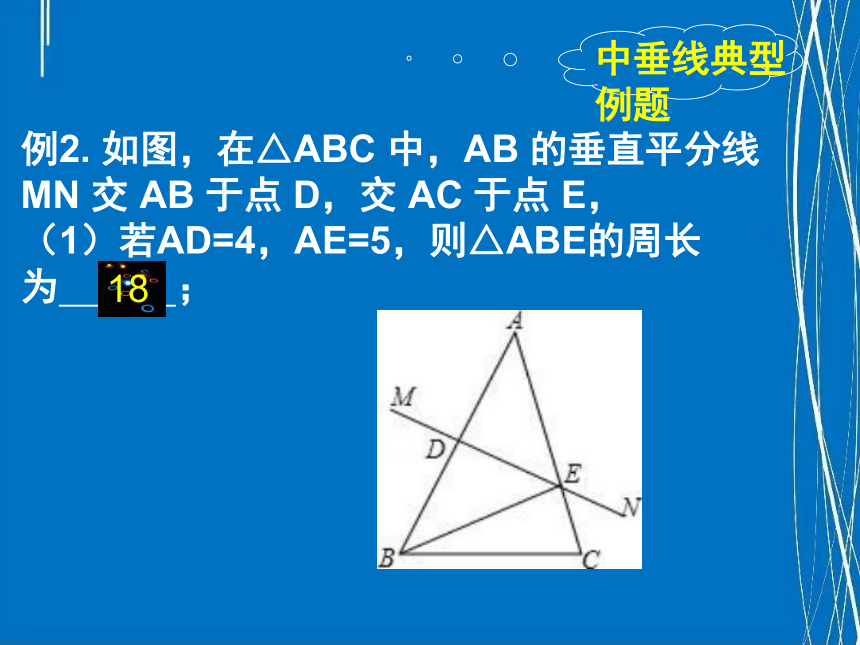
例2. 如图,在△ABC 中,AB 的垂直平分线 MN 交 AB 于点 D,交 AC 于点 E,
(1)若AD=4,AE=5,则△ABE的周长为 ;
18
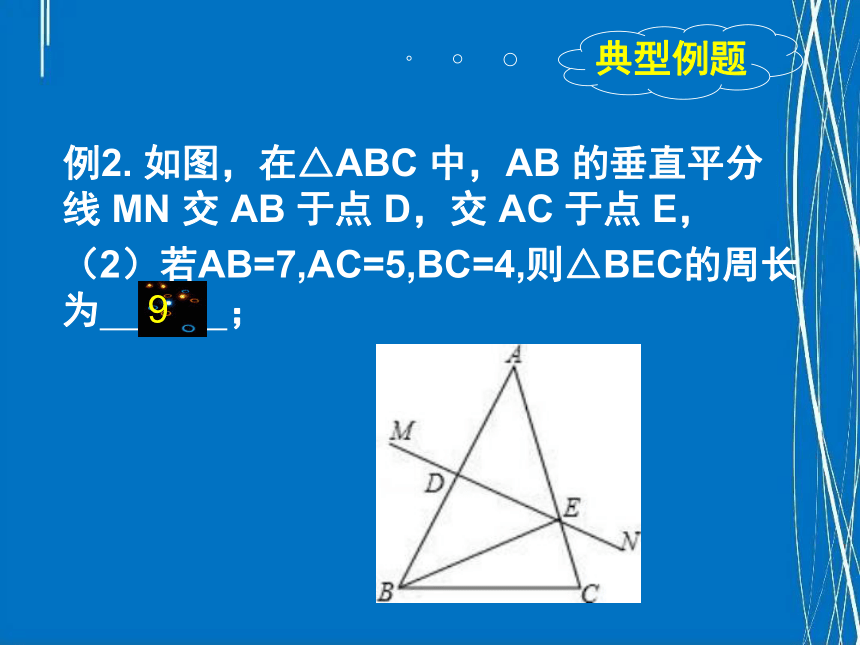
(2)若AB=7,AC=5,BC=4,则△BEC的周长
为 ;
例2. 如图,在△ABC 中,AB 的垂直平分
线 MN 交 AB 于点 D,交 AC 于点 E,
典型例题
9
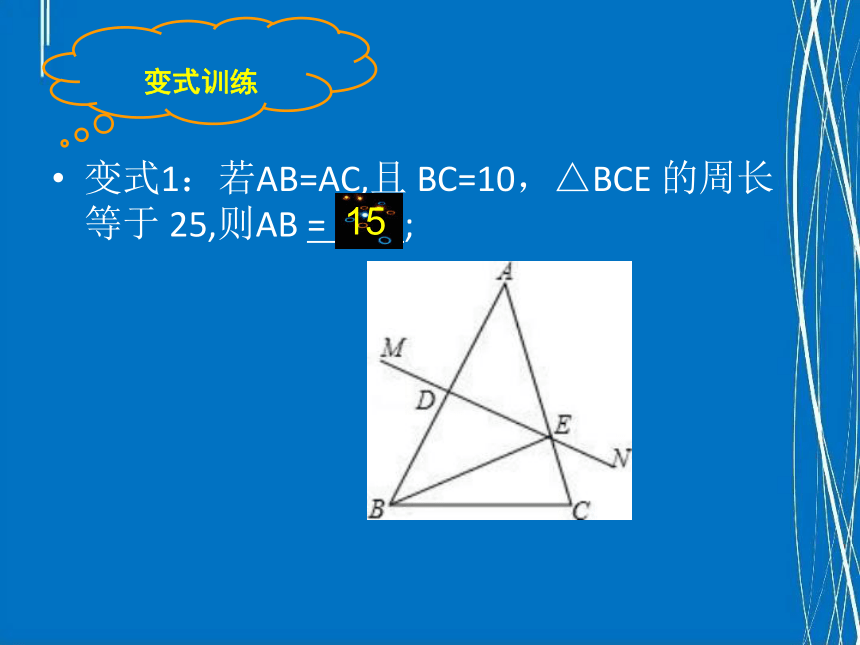
变式1:若AB=AC,且 BC=10,△BCE 的周长等于 25,则AB = ;
变式训练
15
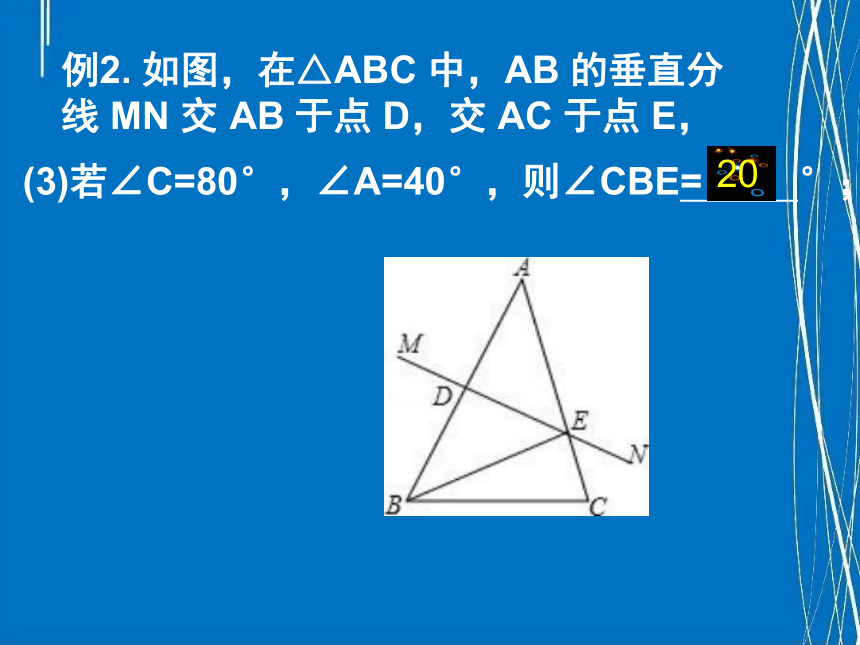
(3)若∠C=80°,∠A=40°,则∠CBE= °;
例2. 如图,在△ABC 中,AB 的垂直分
线 MN 交 AB 于点 D,交 AC 于点 E,
20
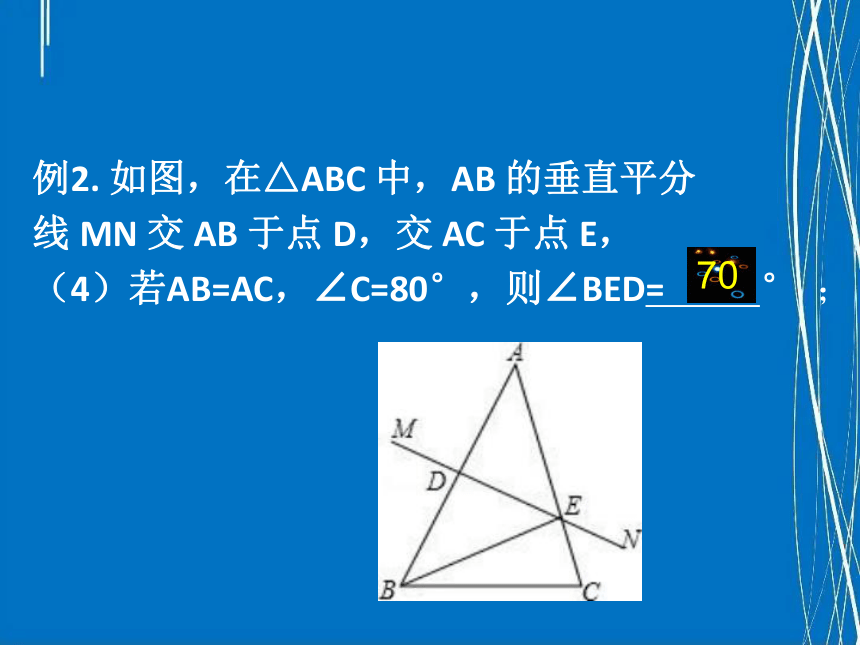
例2. 如图,在△ABC 中,AB 的垂直平分
线 MN 交 AB 于点 D,交 AC 于点 E,
(4)若AB=AC,∠C=80°,则∠BED= ° ;
70
变式2:
①如图,△ABC中,∠A=80°,AB与AC的垂直平分线相交于点P,
则∠PBC = °;
变式训练
A
B
C
P
10
②如图,△ABC中,∠A=80°,AB的垂直平分线分别交BC、AB于
点E和点F,AC的垂直平分线分别交BC、AC与点M和点N ,则
∠MAE= °;
变式训练
N
A
B
C
M
E
F
20
例3.如右图,在△ABC中∠C=90°,BD平
分∠ABC,交AC于点D,DE⊥AB,若AC=a,
AE=b,则△ADE的周= ;
A
B
C
D
E
角平分线典型例题
a+b
变式:如上图在△ABC中∠C=90°,BD平分∠ABC,交AC于点D,若DE垂直平分AB,BC=a,AC=b,AB=c,则△ADE的周长= ;∠A= °.
变式训练
A
B
C
D
E
b+c-a
30
例3 如右图,在△ABC中∠C=90°,BD平分∠ABC,交AC于点D,AD:DC=5:3,AC=8,AB=10,则△ABD的面积= ;
典型例题
A
C
B
D
15
变式:
如右图,在△ABC中∠ABC和∠ACB的角平分线相交于点P,
①若PD⊥BC于D,△ABC的周长为c,PD=h,则△ABC的面积为 ;
②若∠A=80°,则∠BPC= °
变式训练
A
B
C
P
D
1/2ch
130
例4 如图,点D为锐角∠ABC的平分线上一点,点M在边BA上,点N在边BC上,∠BMD+∠BND=180°.试判断DM与DN的数量关系?
典型例题
E
F
变式 :已知∠AOB=90°,OM是∠AOB的角平分线,将三角板的的直角顶点在射线OM上滑动,两直角边分别与OA,OB所在直线交于点C、D,
①如图(1)若点C和点D在射线OA、OB上时,PC和PD有怎样的数量关系?说明理由。
②如图(2)若点C仍在射线OA上,此时点D在射线OB的反向延长线上,则上面的数量关系还成立吗?
变式训练
A
B
O
M
P
C
D
A
B
C
D
M
P
1.你学会了哪些方法?
2.你认为应注意哪些问题?
3.你还有哪些困惑?
思考题
1、如图,∠ABC=90°,且BA=BC,AD∥BC,点E为AB中点,且CE⊥BD,
①求证:BE=AD;
②求证:AC垂直平分ED;
③△BCD是等腰三角形吗?说明理由。
A
B
C
D
E
M
能力过关
2、如图,在△ABC中,AB=AC,过点C作CN∥AB且CN=AC,连接AN交BC于点M.
试说明BC与AN互相垂直平分。
3.(提高题)如图: 点B、C、D、E、F在∠MAN的边上, ∠A=15o, AB=BC=CD=DE=EF,求∠MEF的度数。
A
B
C
D
E
F
M
N
春天不播种,
夏天就不生长,
秋天不能收获,
冬天就不能品尝。
北师大版七年级数学下册
第五章 生活中的轴对称
复习题
一、基础过关
典型例题分析
例1. (1)等腰三角形的一个角是80°,则它的底角 °
80或50
变式1:如果等腰三角形的两个内角的度数之比为1∶4,那么这个三角形的底角
是 °;
变式2:已知等腰三角形一腰上的高与另一
腰的夹角为45°,求其顶角度数为 ;
变式训练
°
80或30
45或135
中垂线典型例题
例2. 如图,在△ABC 中,AB 的垂直平分线 MN 交 AB 于点 D,交 AC 于点 E,
(1)若AD=4,AE=5,则△ABE的周长为 ;
18
(2)若AB=7,AC=5,BC=4,则△BEC的周长
为 ;
例2. 如图,在△ABC 中,AB 的垂直平分
线 MN 交 AB 于点 D,交 AC 于点 E,
典型例题
9
变式1:若AB=AC,且 BC=10,△BCE 的周长等于 25,则AB = ;
变式训练
15
(3)若∠C=80°,∠A=40°,则∠CBE= °;
例2. 如图,在△ABC 中,AB 的垂直分
线 MN 交 AB 于点 D,交 AC 于点 E,
20
例2. 如图,在△ABC 中,AB 的垂直平分
线 MN 交 AB 于点 D,交 AC 于点 E,
(4)若AB=AC,∠C=80°,则∠BED= ° ;
70
变式2:
①如图,△ABC中,∠A=80°,AB与AC的垂直平分线相交于点P,
则∠PBC = °;
变式训练
A
B
C
P
10
②如图,△ABC中,∠A=80°,AB的垂直平分线分别交BC、AB于
点E和点F,AC的垂直平分线分别交BC、AC与点M和点N ,则
∠MAE= °;
变式训练
N
A
B
C
M
E
F
20
例3.如右图,在△ABC中∠C=90°,BD平
分∠ABC,交AC于点D,DE⊥AB,若AC=a,
AE=b,则△ADE的周= ;
A
B
C
D
E
角平分线典型例题
a+b
变式:如上图在△ABC中∠C=90°,BD平分∠ABC,交AC于点D,若DE垂直平分AB,BC=a,AC=b,AB=c,则△ADE的周长= ;∠A= °.
变式训练
A
B
C
D
E
b+c-a
30
例3 如右图,在△ABC中∠C=90°,BD平分∠ABC,交AC于点D,AD:DC=5:3,AC=8,AB=10,则△ABD的面积= ;
典型例题
A
C
B
D
15
变式:
如右图,在△ABC中∠ABC和∠ACB的角平分线相交于点P,
①若PD⊥BC于D,△ABC的周长为c,PD=h,则△ABC的面积为 ;
②若∠A=80°,则∠BPC= °
变式训练
A
B
C
P
D
1/2ch
130
例4 如图,点D为锐角∠ABC的平分线上一点,点M在边BA上,点N在边BC上,∠BMD+∠BND=180°.试判断DM与DN的数量关系?
典型例题
E
F
变式 :已知∠AOB=90°,OM是∠AOB的角平分线,将三角板的的直角顶点在射线OM上滑动,两直角边分别与OA,OB所在直线交于点C、D,
①如图(1)若点C和点D在射线OA、OB上时,PC和PD有怎样的数量关系?说明理由。
②如图(2)若点C仍在射线OA上,此时点D在射线OB的反向延长线上,则上面的数量关系还成立吗?
变式训练
A
B
O
M
P
C
D
A
B
C
D
M
P
1.你学会了哪些方法?
2.你认为应注意哪些问题?
3.你还有哪些困惑?
思考题
1、如图,∠ABC=90°,且BA=BC,AD∥BC,点E为AB中点,且CE⊥BD,
①求证:BE=AD;
②求证:AC垂直平分ED;
③△BCD是等腰三角形吗?说明理由。
A
B
C
D
E
M
能力过关
2、如图,在△ABC中,AB=AC,过点C作CN∥AB且CN=AC,连接AN交BC于点M.
试说明BC与AN互相垂直平分。
3.(提高题)如图: 点B、C、D、E、F在∠MAN的边上, ∠A=15o, AB=BC=CD=DE=EF,求∠MEF的度数。
A
B
C
D
E
F
M
N
春天不播种,
夏天就不生长,
秋天不能收获,
冬天就不能品尝。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
