七年级数学苏科版下册10.1 二元一次方程 课件(共23张PPT)
文档属性
| 名称 | 七年级数学苏科版下册10.1 二元一次方程 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 909.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-05 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
根据篮球比赛规则:赢一场得2分,输一场得1分.在某次中学生篮球联赛中,一支球队,赢了若干场后积20分,问该球队赢了多少场 输了多少场
想一想:
10.1 二元一次方程
教学目标:
1、掌握二元一次方程、二元一次方程的解的含义,并会检验一对数是不是某个二元一次方程的解;
2、通过练习和讨论,进一步提高观察、比较、分析问题的能力.
根据篮球比赛规则:赢一场得2分,输一场得1分.在某次中学生篮球联赛中,一支球队,赢了若干场后积20分,问该球队赢了多少场 输了多少场
如果设该队赢了x场,输了y场,那么请你填写下表:
场 数 每场得分 积 分
赢
输
这些量存在什么样的相等关系
可以用什么式子表达问题中的相等的量
2x+y=20
x
2
2x
y
1
y
某球员在一场篮球比赛中共得35分(其中罚球得10分).问:他分别投中了多少个两分球和三分球
考考你
设他投中了x个两分球、y个三分球,那么
2x+3y=35-10,
即 2x+3y=25.
问题古今
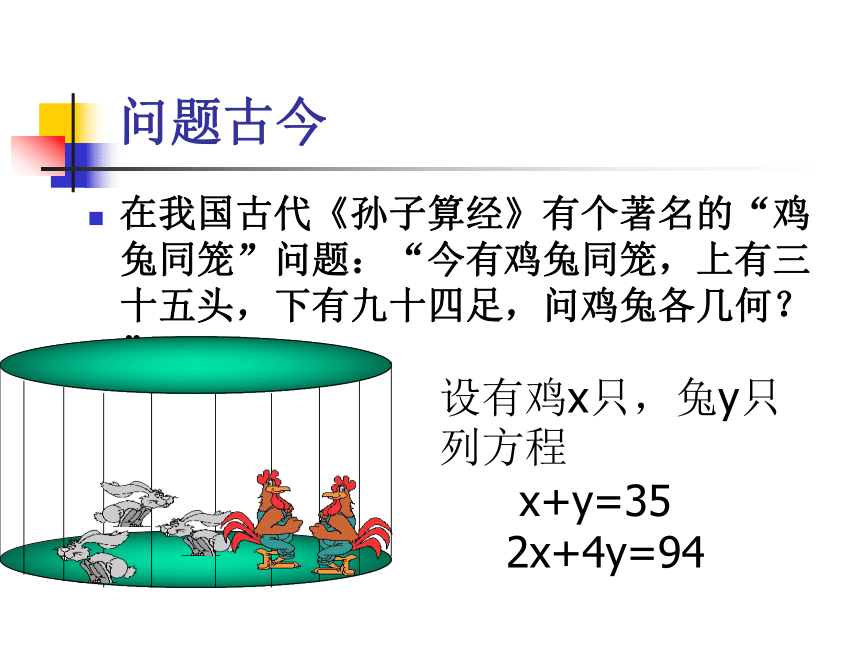
在我国古代《孙子算经》有个著名的“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
设有鸡x只,兔y只
列方程
x+y=35
2x+4y=94
议一议:
2x+y=20 2x+3y=25
x+y=35 2x+4y=94
观察上面四个方程,是否为一元一次方程
如果不是,那么这四个方程有什么共同特点
一元一次方
程的概念:
只含有一个未知数(元)且
未知数的指数是1(次) ,这样的
整式方程叫做一元一次方程。
温故知新:
二元一次方
程的概念:
①含有两个未知数(元)并且
②所含未知数的项的次数都为1
③这样的整式方程叫做二元一次方程。
2x+y=20 2x+3y=25
x+y=35 2x+4y=94
含有两个未知数,并且含未知数的项的次数为1的整式方程叫二元一次方程。
判断:下列哪些是二元一次方程,哪些不是?
(1)
(2)
(3)
(4)
(5)
(6)
(8)
不是
是
不是
不是
不是
不是
不是
是
(7) π+y=4
含有两个未知数,并且含未知数的项的次数为1的整式方程叫二元一次方程。
例1、若2x2m+3+3yn-1=0是二元一次方程,
求m、 n值
解:根据题意得,
2m+3=1 n-1=1
m=-1 n=2
含有两个未知数,并且含未知数的项的次数为1的整式方程叫二元一次方程。
练一练
已知:5x3m+7-2y2n-1=4是二元一次方程,求m、n的值
学以致用
已知: 是二元一次方程。
求 。
解:
根据题意得
认真思考
根据下列语句,分别设适当的未知数,列出二元一次方程:
1.甲数比乙数大3.设甲数为x,乙数为y;
2.一个长方形的周长是20cm.设这个长方形的长是xcm,宽是ycm;
3.甲、乙两人各工作5天,共生产零件80件.设甲每天生产零件x件,乙每天生产零件y件.
x-y=3
2x+2y=20
5x+5y=80
你能编拟一个所列方程为:2x+y=5
的实际问题吗?
自由发挥
(1)用关于x的代数式表示y .
(2)用关于y的代数式表示x .
温故知新:
二元一次方程
解的概念:
使二元一次方程两边相等一对未知数的值,叫做二元一次方程的解。
x=a
y=b
如x=8,y=3就是方程2x+3y=25的一个解,记作
一般一个二
元一次方程有
无数组解
一元一次方程
解的概念:
使一元一次方程两边相等的未知数的值,叫做一元一次方程的解。
解的表示方法:
使二元一次方程左右两边的值相等的一对未知数的值叫二元一次方程的解。
例如: 是方程 的一个解
记作:
判断: 四对数值中,哪几对
是二元一次方程 的解?
当 时,左边= =右边
∴ 是二元一次方程 的解
使二元一次方程左右两边的值相等
的一对未知数的值叫二元一次方程的解
思考:对于方程 ,给你一个x的值,你可以求出y的值吗?
当x=-3时,y= , 当y=1时,x= 。
x可以取无数个值,因此,方程 有 对解。
一般地,二元一次方程的解有无数对。
使二元一次方程左右两边的值相等的
一对未知数的值叫二元一次方程的解
对于方程 ,当它的一组解中的x、y的值都是
正整数时,称这组解是方程的正整数解。
求方程 的正整数解。
考考你
使二元一次方程左右两边的值相等的
一对未知数的值叫二元一次方程的解
是方程 的一个解,求 。
解:把 代入方程得
巩固新知:
变式
是方程 的一个解,求 。
尝试解决:
这节课,我的收获是---
小结与回顾
课堂小结:
1、二元一次方程:2个未知数;含未知数的项次数为1;整式方程
2、二元一次方程的解
3、通过列表可以求某些二元一次方程的正整数解(非负整数解、非正整数解)。
书 P95 1.2.3.
作业:
根据篮球比赛规则:赢一场得2分,输一场得1分.在某次中学生篮球联赛中,一支球队,赢了若干场后积20分,问该球队赢了多少场 输了多少场
想一想:
10.1 二元一次方程
教学目标:
1、掌握二元一次方程、二元一次方程的解的含义,并会检验一对数是不是某个二元一次方程的解;
2、通过练习和讨论,进一步提高观察、比较、分析问题的能力.
根据篮球比赛规则:赢一场得2分,输一场得1分.在某次中学生篮球联赛中,一支球队,赢了若干场后积20分,问该球队赢了多少场 输了多少场
如果设该队赢了x场,输了y场,那么请你填写下表:
场 数 每场得分 积 分
赢
输
这些量存在什么样的相等关系
可以用什么式子表达问题中的相等的量
2x+y=20
x
2
2x
y
1
y
某球员在一场篮球比赛中共得35分(其中罚球得10分).问:他分别投中了多少个两分球和三分球
考考你
设他投中了x个两分球、y个三分球,那么
2x+3y=35-10,
即 2x+3y=25.
问题古今
在我国古代《孙子算经》有个著名的“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”
设有鸡x只,兔y只
列方程
x+y=35
2x+4y=94
议一议:
2x+y=20 2x+3y=25
x+y=35 2x+4y=94
观察上面四个方程,是否为一元一次方程
如果不是,那么这四个方程有什么共同特点
一元一次方
程的概念:
只含有一个未知数(元)且
未知数的指数是1(次) ,这样的
整式方程叫做一元一次方程。
温故知新:
二元一次方
程的概念:
①含有两个未知数(元)并且
②所含未知数的项的次数都为1
③这样的整式方程叫做二元一次方程。
2x+y=20 2x+3y=25
x+y=35 2x+4y=94
含有两个未知数,并且含未知数的项的次数为1的整式方程叫二元一次方程。
判断:下列哪些是二元一次方程,哪些不是?
(1)
(2)
(3)
(4)
(5)
(6)
(8)
不是
是
不是
不是
不是
不是
不是
是
(7) π+y=4
含有两个未知数,并且含未知数的项的次数为1的整式方程叫二元一次方程。
例1、若2x2m+3+3yn-1=0是二元一次方程,
求m、 n值
解:根据题意得,
2m+3=1 n-1=1
m=-1 n=2
含有两个未知数,并且含未知数的项的次数为1的整式方程叫二元一次方程。
练一练
已知:5x3m+7-2y2n-1=4是二元一次方程,求m、n的值
学以致用
已知: 是二元一次方程。
求 。
解:
根据题意得
认真思考
根据下列语句,分别设适当的未知数,列出二元一次方程:
1.甲数比乙数大3.设甲数为x,乙数为y;
2.一个长方形的周长是20cm.设这个长方形的长是xcm,宽是ycm;
3.甲、乙两人各工作5天,共生产零件80件.设甲每天生产零件x件,乙每天生产零件y件.
x-y=3
2x+2y=20
5x+5y=80
你能编拟一个所列方程为:2x+y=5
的实际问题吗?
自由发挥
(1)用关于x的代数式表示y .
(2)用关于y的代数式表示x .
温故知新:
二元一次方程
解的概念:
使二元一次方程两边相等一对未知数的值,叫做二元一次方程的解。
x=a
y=b
如x=8,y=3就是方程2x+3y=25的一个解,记作
一般一个二
元一次方程有
无数组解
一元一次方程
解的概念:
使一元一次方程两边相等的未知数的值,叫做一元一次方程的解。
解的表示方法:
使二元一次方程左右两边的值相等的一对未知数的值叫二元一次方程的解。
例如: 是方程 的一个解
记作:
判断: 四对数值中,哪几对
是二元一次方程 的解?
当 时,左边= =右边
∴ 是二元一次方程 的解
使二元一次方程左右两边的值相等
的一对未知数的值叫二元一次方程的解
思考:对于方程 ,给你一个x的值,你可以求出y的值吗?
当x=-3时,y= , 当y=1时,x= 。
x可以取无数个值,因此,方程 有 对解。
一般地,二元一次方程的解有无数对。
使二元一次方程左右两边的值相等的
一对未知数的值叫二元一次方程的解
对于方程 ,当它的一组解中的x、y的值都是
正整数时,称这组解是方程的正整数解。
求方程 的正整数解。
考考你
使二元一次方程左右两边的值相等的
一对未知数的值叫二元一次方程的解
是方程 的一个解,求 。
解:把 代入方程得
巩固新知:
变式
是方程 的一个解,求 。
尝试解决:
这节课,我的收获是---
小结与回顾
课堂小结:
1、二元一次方程:2个未知数;含未知数的项次数为1;整式方程
2、二元一次方程的解
3、通过列表可以求某些二元一次方程的正整数解(非负整数解、非正整数解)。
书 P95 1.2.3.
作业:
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
