5.1.1变化率问题 课件(共27张PPT)
文档属性
| 名称 | 5.1.1变化率问题 课件(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 08:11:10 | ||
图片预览








文档简介
(共27张PPT)
5.1导数的概念及其意义
5.1.1变化率问题
在必修第一册中,我们研究了函数的单调性,并利用函数单调性等知识定性地研究了一次函数、指数函数、对数函数增长速度的差异,知道“对数增长”是越来越慢的,“指数爆炸”比“直线上升”快得多.进一步地,能否精确定量地刻画变化速度的快慢呢?下面我们就来研究这个问题.
在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系
如何描述运动员从起跳到入水的过程中运动的快慢程度呢?
直觉告诉我们,运动员从起跳到入水的过程中,在上升阶段运动得越来越慢,在下降阶段运动得越来越快.
我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度 近似地描述他的运动状态
问题1 高台跳水
在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系
问题1 高台跳水
答: (1)不是。先上升,后下降。
(2)平均速度只能粗略的描述运动员的运动状态,它并不能反映某一刻的运动状态。
(1)运动员在这段时间里是静止的吗?
0m/s
(2)你认为用平均速度描述运动员的
运动状态有什么问题?
探究
我们把物体在某一时刻的速度称为瞬时速度.
探究
瞬时速度与平均速度有什么关系?你能利用这种关系求运动员在t=1s时的瞬时速度吗?
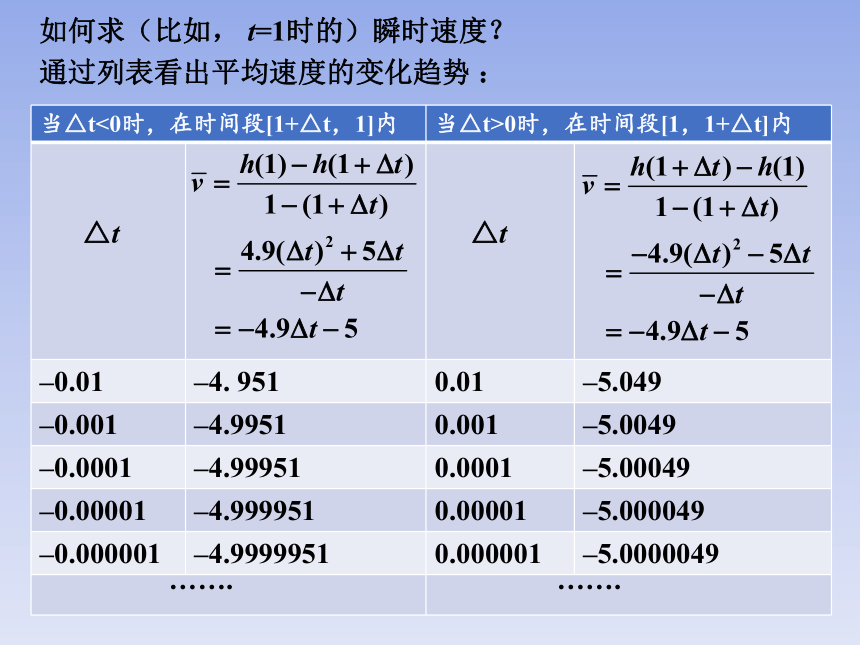
当△t<0时,在时间段[1+△t,1]内 当△t>0时,在时间段[1,1+△t]内
△t
△t
–0.01 –4. 951 0.01 –5.049
–0.001 –4.9951 0.001 –5.0049
–0.0001 –4.99951 0.0001 –5.00049
–0.00001 –4.999951 0.00001 –5.000049
–0.000001 –4.9999951 0.000001 –5.0000049
…….
…….
如何求(比如, t=1时的)瞬时速度?
通过列表看出平均速度的变化趋势 :
观察
思考
问题2 抛物线的切线的斜率
探究
设曲线C是函数 y=f(x) 的图象,
在曲线C上取一点 P0及P0点邻近的任一点
P(x0+△x,y0+△y) , 过P0,P两点作割线,
则直线P0P的斜率为
上面我们研究了切线的斜率问题,
可以将以上的过程概括如下:
–0.01 1.99 0.01 2.01
–0.001 1.999 0.001 2.001
–0.0001 1.9999 0.0001 2.0002
–0.00001 1.99999 0.00001 2.00001
–0.000001 1.999999 0.000001 2.000001
……. …….
观察
思考
P
相切
相交
再来一次
P
P0
P
P
T
再来一次
当直线P0P转动时, P逐渐向P0靠近,
也即△x 变小
当△x→0时, P0P无限靠近P0 T
因此:
一般地,
函数y=f(x)在x=x0处的瞬时变化率是
上式称为函数y=f(x)在x=x0处的导数
记作: 或
即
注意:
1、函数应在点的附近有定义,
否则导数不存在。
2、在定义导数的极限式中,△x趋近于0
可正、可负,但不为0,而△y可能为0。
3、导数是一个局部概念,它只与函数在x0
及其附近的函数值有关,与△x无关。
4、若极限 不存在,则称
函数在点x0处不可导。
物体的运动方程 s=s(t)在t0处的导数
即在t0处的瞬时速度vt0
函数y=f(x)在x0处的导数
即曲线在x0处的切线斜率.
导数可以描述任何事物的瞬时变化率.
瞬时变化率除了瞬时速度,切线的斜率
还有:点密度,国内生产总值(GDP)的增
长率,经济学上讲的一切边际量
等.
课堂练习
课堂练习
Thank you for watching !
5.1导数的概念及其意义
5.1.1变化率问题
在必修第一册中,我们研究了函数的单调性,并利用函数单调性等知识定性地研究了一次函数、指数函数、对数函数增长速度的差异,知道“对数增长”是越来越慢的,“指数爆炸”比“直线上升”快得多.进一步地,能否精确定量地刻画变化速度的快慢呢?下面我们就来研究这个问题.
在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系
如何描述运动员从起跳到入水的过程中运动的快慢程度呢?
直觉告诉我们,运动员从起跳到入水的过程中,在上升阶段运动得越来越慢,在下降阶段运动得越来越快.
我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度 近似地描述他的运动状态
问题1 高台跳水
在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系
问题1 高台跳水
答: (1)不是。先上升,后下降。
(2)平均速度只能粗略的描述运动员的运动状态,它并不能反映某一刻的运动状态。
(1)运动员在这段时间里是静止的吗?
0m/s
(2)你认为用平均速度描述运动员的
运动状态有什么问题?
探究
我们把物体在某一时刻的速度称为瞬时速度.
探究
瞬时速度与平均速度有什么关系?你能利用这种关系求运动员在t=1s时的瞬时速度吗?
当△t<0时,在时间段[1+△t,1]内 当△t>0时,在时间段[1,1+△t]内
△t
△t
–0.01 –4. 951 0.01 –5.049
–0.001 –4.9951 0.001 –5.0049
–0.0001 –4.99951 0.0001 –5.00049
–0.00001 –4.999951 0.00001 –5.000049
–0.000001 –4.9999951 0.000001 –5.0000049
…….
…….
如何求(比如, t=1时的)瞬时速度?
通过列表看出平均速度的变化趋势 :
观察
思考
问题2 抛物线的切线的斜率
探究
设曲线C是函数 y=f(x) 的图象,
在曲线C上取一点 P0及P0点邻近的任一点
P(x0+△x,y0+△y) , 过P0,P两点作割线,
则直线P0P的斜率为
上面我们研究了切线的斜率问题,
可以将以上的过程概括如下:
–0.01 1.99 0.01 2.01
–0.001 1.999 0.001 2.001
–0.0001 1.9999 0.0001 2.0002
–0.00001 1.99999 0.00001 2.00001
–0.000001 1.999999 0.000001 2.000001
……. …….
观察
思考
P
相切
相交
再来一次
P
P0
P
P
T
再来一次
当直线P0P转动时, P逐渐向P0靠近,
也即△x 变小
当△x→0时, P0P无限靠近P0 T
因此:
一般地,
函数y=f(x)在x=x0处的瞬时变化率是
上式称为函数y=f(x)在x=x0处的导数
记作: 或
即
注意:
1、函数应在点的附近有定义,
否则导数不存在。
2、在定义导数的极限式中,△x趋近于0
可正、可负,但不为0,而△y可能为0。
3、导数是一个局部概念,它只与函数在x0
及其附近的函数值有关,与△x无关。
4、若极限 不存在,则称
函数在点x0处不可导。
物体的运动方程 s=s(t)在t0处的导数
即在t0处的瞬时速度vt0
函数y=f(x)在x0处的导数
即曲线在x0处的切线斜率.
导数可以描述任何事物的瞬时变化率.
瞬时变化率除了瞬时速度,切线的斜率
还有:点密度,国内生产总值(GDP)的增
长率,经济学上讲的一切边际量
等.
课堂练习
课堂练习
Thank you for watching !
