5.2.1基本初等函数的导数 课件(共29张PPT)
文档属性
| 名称 | 5.2.1基本初等函数的导数 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 921.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 08:41:40 | ||
图片预览








文档简介
(共29张PPT)
5.2 导数的运算
5.2.1 基本初等函数的导数
一、复习
导数的几何意义
导数的物理物理意义
2.求函数的导数的方法是:
说明:上面的方法中把x换x0即为求函数在点x0处的 导数.
二、几种常见函数的导数
根据导数的定义可以得出一些常见函数的导数公式.
1.函数 y = f (x) =c 的导数
y=c
y
x
O
y =0表示函数y=x图象上每一点处的切线的斜率都为0.
若y=c表示路程关于时间的函数,则y =0则为某物体的瞬时速度始终为0,即一直处于静止状态.
从几何的角度理解:
从物理的角度理解:
2.函数 y= f (x)=x 的导数
y=x
y
x
O
y =1表示函数y=x图象上每一点处的切线斜率都为1.
若y=x表示路程关于时间的函数,则y =1可以解释为某物体做瞬时速度为1的匀速运动.
从几何的角度理解:
从物理的角度理解:
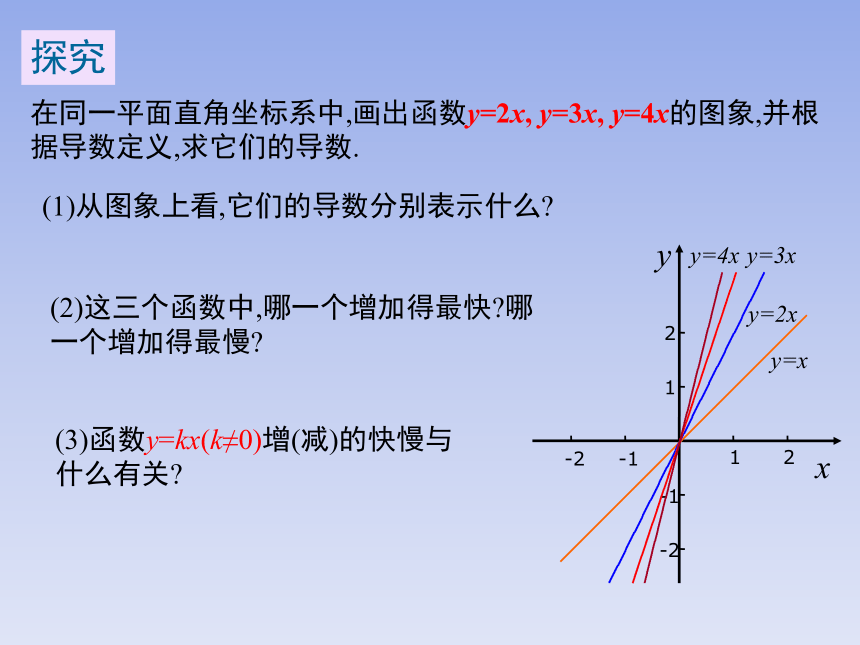
在同一平面直角坐标系中,画出函数y=2x, y=3x, y=4x的图象,并根据导数定义,求它们的导数.
(1)从图象上看,它们的导数分别表示什么
(2)这三个函数中,哪一个增加得最快 哪一个增加得最慢
(3)函数y=kx(k≠0)增(减)的快慢与什么有关
2
1
-1
-2
-2
-1
1
2
x
y
y=x
y=2x
y=3x
y=4x
探究
函数 y= f (x)= kx 的导数
3.函数 y = f (x) = x2 的导数
y=x2
y
x
O
y =2x表示函数y=x2图象上点(x,y)处切线的斜率为2x,说明随着x的变化,切线的斜率也在变化.
从导数作为函数在一点的瞬时变化率来看,y =2x表明: 当x<0时,随着x的增加, | y |越来越小, y=x2减少得越来越慢; 当x>0时,随着x的增加, | y |越来越大, y=x2增加得越来越快.
从几何的角度理解:
从物理的角度理解:
若y=x2表示路程关于时间的函数,则y =2x可以解释为某物体作变速运动,它在时刻x的瞬时速度为2x.
由函数y=x ,y=x2 ,y=x3的导数为
你猜测 y = xn 导数是什么
y' =nxn-1
1,2x,3x2
P
l
能否将圆的切线的概念推广为一般曲线的切线:直线与曲线有唯一公共点时,直线叫曲线过该点的切线?如果能,请说明理由;如果不能,请举出反例。
不能
x
y
o
直线与圆有惟一公共点时,
直线叫做圆的切线。
所以,不能用直线与曲线的公共点的个数来定义曲线的切线。
圆的切线定义并不适用于一般的曲线。
通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
2
1
-1
-2
-2
-1
1
2
x
y
探究
小结
推广:
例1 求下列函数的导数:
解:根据基本初等函数的导数公式表,有
所以,在第10个年头,这种商品的价格约以0.08元/年的速度上涨.
例2、y=|x|(x∈R)有没有导函数,试求之。
解: (1)当x>0时,y=x, 则y' =1
(2)当x<0时,y=-x,不难求得y' =-1
(3)当x=0时,y=0,求其导数如下:
当△x>0时,比值为1,从而极限为1
当△x<0时,比值为-1,从而极限为-1
从而当x=0时,极限不存在。
故y=|x|(x∈R)没有导函数。
课堂练习
1.求下列函数的导数:
课堂练习
2.求下列函数在给定点的导数:
四、小结:
知识点:
基本初等函数的导数公式、导数的运算法则
能力要求:
(1)熟记这些公式、法则;
(2)会求简单函数的导数;
(3)会求曲线在某点处的切线方程。
课后思考:
如何求函数 的导数
Thank you for watching !
导数的运算法则:
法则1:两个函数的和(差)的导数,等于这两个函数的导数的
和(差),即:
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:
法则3:两个函数的积的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:
例. 求函数y=x3-2x2+3的导数.
推论:
5.2 导数的运算
5.2.1 基本初等函数的导数
一、复习
导数的几何意义
导数的物理物理意义
2.求函数的导数的方法是:
说明:上面的方法中把x换x0即为求函数在点x0处的 导数.
二、几种常见函数的导数
根据导数的定义可以得出一些常见函数的导数公式.
1.函数 y = f (x) =c 的导数
y=c
y
x
O
y =0表示函数y=x图象上每一点处的切线的斜率都为0.
若y=c表示路程关于时间的函数,则y =0则为某物体的瞬时速度始终为0,即一直处于静止状态.
从几何的角度理解:
从物理的角度理解:
2.函数 y= f (x)=x 的导数
y=x
y
x
O
y =1表示函数y=x图象上每一点处的切线斜率都为1.
若y=x表示路程关于时间的函数,则y =1可以解释为某物体做瞬时速度为1的匀速运动.
从几何的角度理解:
从物理的角度理解:
在同一平面直角坐标系中,画出函数y=2x, y=3x, y=4x的图象,并根据导数定义,求它们的导数.
(1)从图象上看,它们的导数分别表示什么
(2)这三个函数中,哪一个增加得最快 哪一个增加得最慢
(3)函数y=kx(k≠0)增(减)的快慢与什么有关
2
1
-1
-2
-2
-1
1
2
x
y
y=x
y=2x
y=3x
y=4x
探究
函数 y= f (x)= kx 的导数
3.函数 y = f (x) = x2 的导数
y=x2
y
x
O
y =2x表示函数y=x2图象上点(x,y)处切线的斜率为2x,说明随着x的变化,切线的斜率也在变化.
从导数作为函数在一点的瞬时变化率来看,y =2x表明: 当x<0时,随着x的增加, | y |越来越小, y=x2减少得越来越慢; 当x>0时,随着x的增加, | y |越来越大, y=x2增加得越来越快.
从几何的角度理解:
从物理的角度理解:
若y=x2表示路程关于时间的函数,则y =2x可以解释为某物体作变速运动,它在时刻x的瞬时速度为2x.
由函数y=x ,y=x2 ,y=x3的导数为
你猜测 y = xn 导数是什么
y' =nxn-1
1,2x,3x2
P
l
能否将圆的切线的概念推广为一般曲线的切线:直线与曲线有唯一公共点时,直线叫曲线过该点的切线?如果能,请说明理由;如果不能,请举出反例。
不能
x
y
o
直线与圆有惟一公共点时,
直线叫做圆的切线。
所以,不能用直线与曲线的公共点的个数来定义曲线的切线。
圆的切线定义并不适用于一般的曲线。
通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
2
1
-1
-2
-2
-1
1
2
x
y
探究
小结
推广:
例1 求下列函数的导数:
解:根据基本初等函数的导数公式表,有
所以,在第10个年头,这种商品的价格约以0.08元/年的速度上涨.
例2、y=|x|(x∈R)有没有导函数,试求之。
解: (1)当x>0时,y=x, 则y' =1
(2)当x<0时,y=-x,不难求得y' =-1
(3)当x=0时,y=0,求其导数如下:
当△x>0时,比值为1,从而极限为1
当△x<0时,比值为-1,从而极限为-1
从而当x=0时,极限不存在。
故y=|x|(x∈R)没有导函数。
课堂练习
1.求下列函数的导数:
课堂练习
2.求下列函数在给定点的导数:
四、小结:
知识点:
基本初等函数的导数公式、导数的运算法则
能力要求:
(1)熟记这些公式、法则;
(2)会求简单函数的导数;
(3)会求曲线在某点处的切线方程。
课后思考:
如何求函数 的导数
Thank you for watching !
导数的运算法则:
法则1:两个函数的和(差)的导数,等于这两个函数的导数的
和(差),即:
法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:
法则3:两个函数的积的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:
例. 求函数y=x3-2x2+3的导数.
推论:
