5.3.1函数的单调性与导数 课件(共24张PPT)
文档属性
| 名称 | 5.3.1函数的单调性与导数 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 08:51:26 | ||
图片预览


文档简介
(共24张PPT)
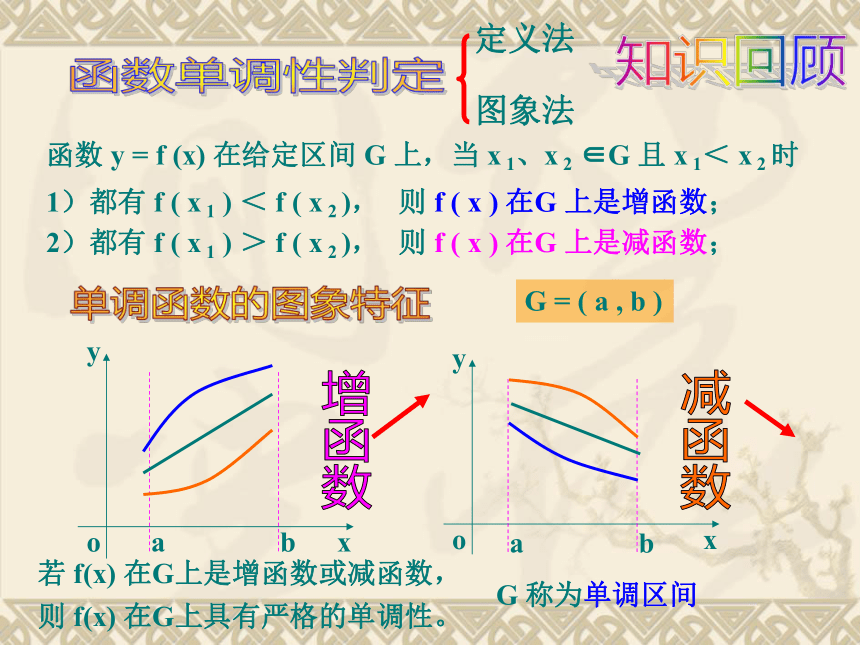
函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时
y
x
o
a
b
y
x
o
a
b
1)都有 f ( x 1 ) < f ( x 2 ),
则 f ( x ) 在G 上是增函数;
2)都有 f ( x 1 ) > f ( x 2 ),
则 f ( x ) 在G 上是减函数;
若 f(x) 在G上是增函数或减函数,
则 f(x) 在G上具有严格的单调性。
G 称为单调区间
G = ( a , b )
定义法
图象法
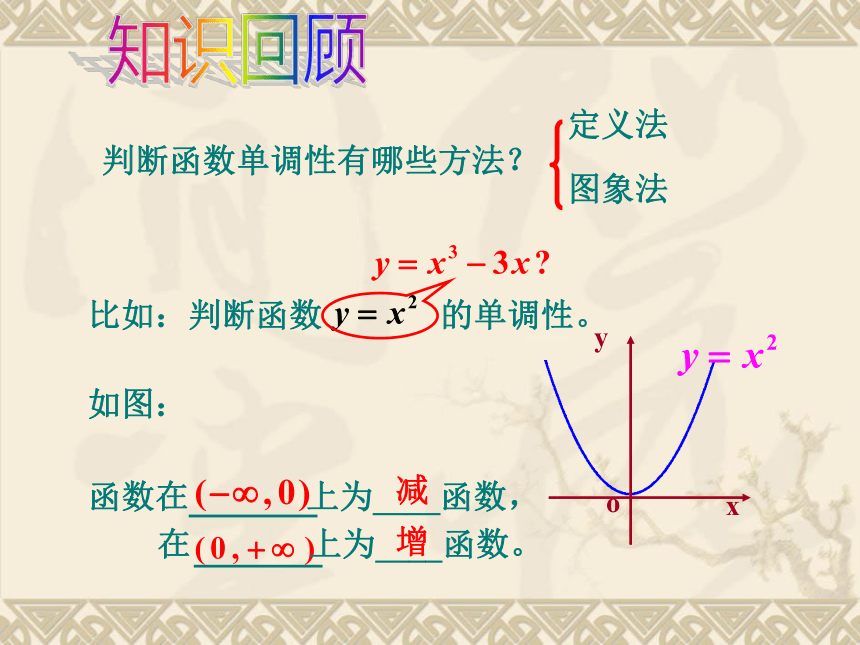
判断函数单调性有哪些方法?
比如:判断函数 的单调性。
x
y
o
函数在 上为____函数,
在 上为____函数。
图象法
定义法
减
增
如图:
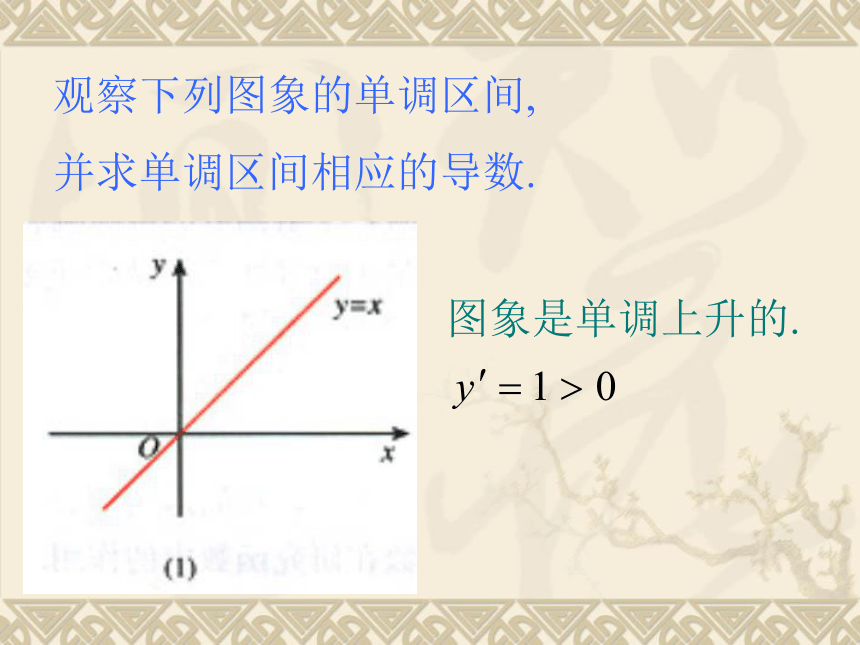
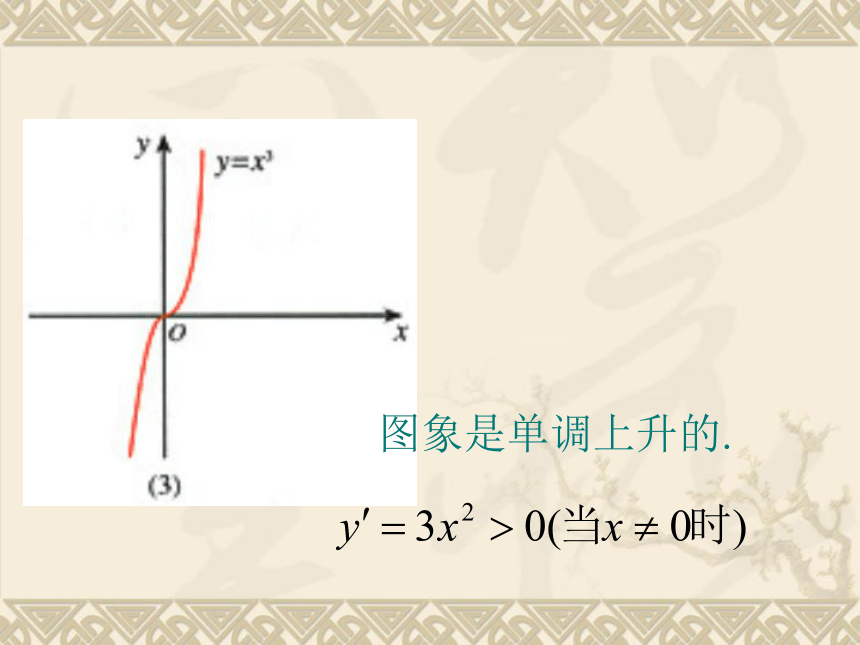
图象是单调上升的.
观察下列图象的单调区间,
并求单调区间相应的导数.
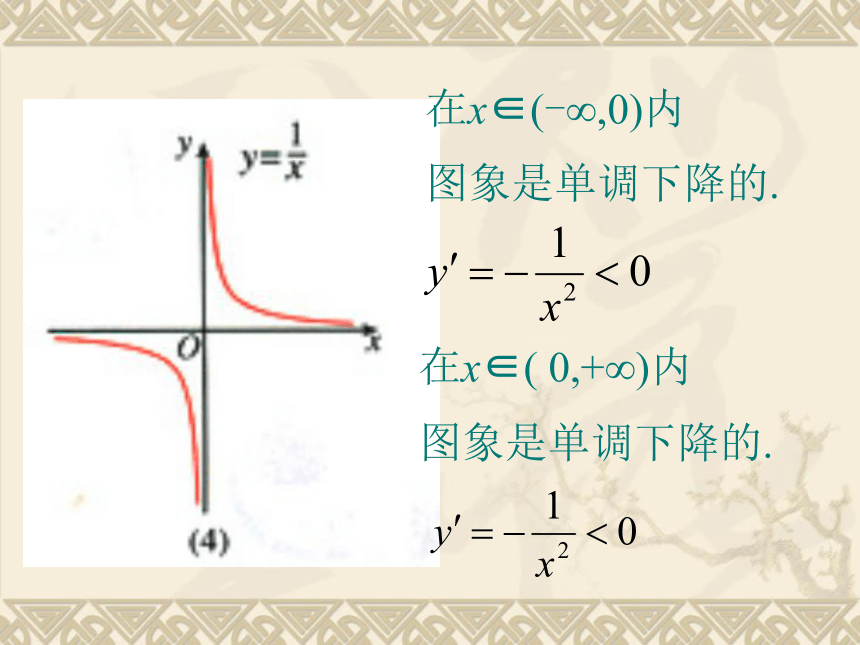
图象是单调下降的.
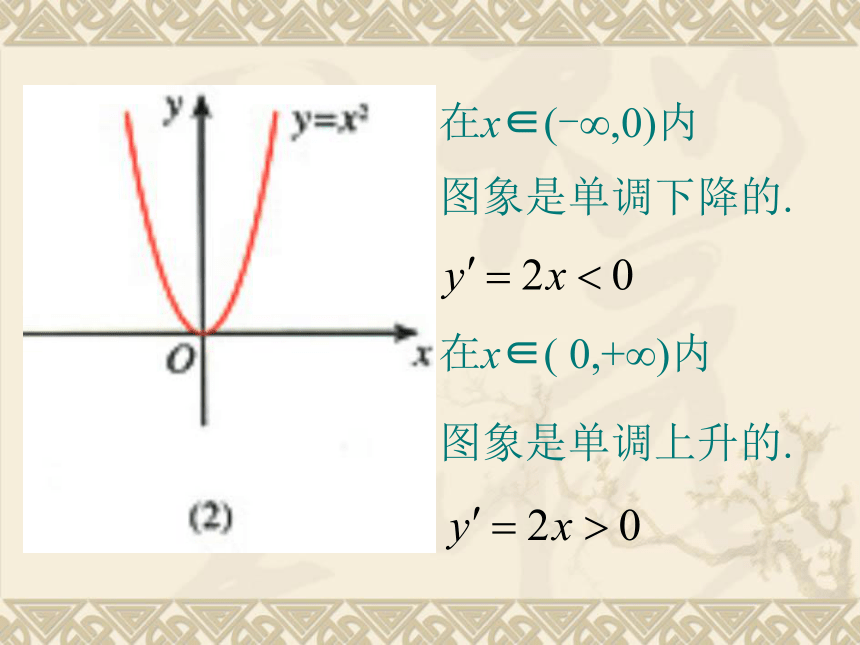
在x∈(-∞,0)内
图象是单调上升的.
在x∈( 0,+∞)内
图象是单调上升的.
图象是单调下降的.
在x∈(-∞,0)内
图象是单调下降的.
在x∈( 0,+∞)内
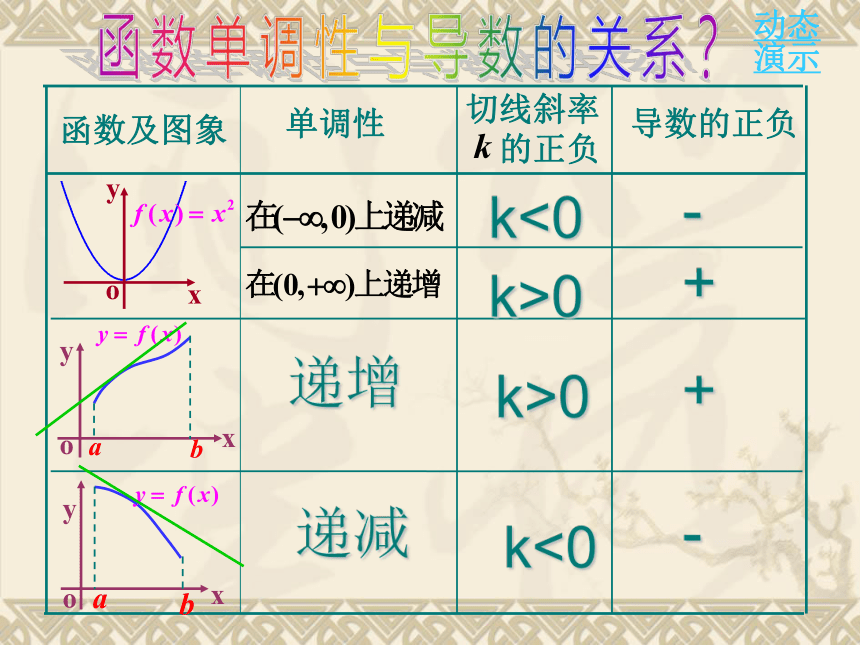
函数的单调性与其导函数正负的关系:
当函数y=f (x)在某个区间内可导时,
如果 , 则f (x)为增函数;
如果 , 则f (x)为减函数。
动态
演示
单调性
导数的正负
函数及图象
x
y
o
x
y
o
切线斜率
的正负
x
y
o
k>0
k>0
k<0
k<0
+
+
-
-
递增
递减
注意:
应正确理解 “ 某个区间 ” 的含义, 它必是定义域内的某个区间。
如果在某个区间内恒有 =0 ,则f(x)为常数函数.
例1、已知导函数 的下列信息:
当10
当x>4,或x<1时, <0
当x=4,或x=1时, =0
试画出函数f(x)图象的大致形状。
4
1
解:由题意可知
当1f(x)为增函数
当x>4,或x<1时,
f(x)为减函数
当x=4,或x=1时,
两点为“临界点”
其图象的大致形状如图。
例2、判断下列函数的单调性,并求出
单调区间:
(1) f(x)=x3+3x ;
解: =3x2+3=3(x2+1)>0
从而函数f(x)=x3+3x
在x∈R上单调递增,
见右图。
(2) f(x)=x2-2x-3 ;
解: =2x-2=2(x-1)>0
图象见右图。
当 >0,即x>1时,函数单调递增;
当 <0,即x<1时,
函数单调递减;
(3) f(x)=sinx-x ; x∈(0,p)
解: =cosx-1<0
从而函数f(x)=sinx-x
在x∈(0, )单调递减,
见右图。
(4) f(x)=2x3+3x2-24x+1 ;
解: =6x2+6x-24=6(x2+x-4)>0
当 >0,
即 时,
函数单调递增;
图象见右图。
当 <0,
即 时,
函数单调递减;
例3 如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.
(A)
(B)
(C)
(D)
h
t
O
h
t
O
h
t
O
h
t
O
(1)
(2)
(3)
(4)
(1)→(B),(2)→(A),(3)→(D),(4)→(C)
总结: 当遇到三次或三次以上的,或图象很难
画出的函数求单调性问题时,应考虑导数法。
①求定义域
②求
③令
④做出结论
1°什么情况下,用“导数法” 求函数单调性、
单调区间较简便?
2°试总结用“导数法” 求单调区间的步骤?
(04年全国理)
B
x
y
o
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
2
(A)
(B)
(C)
(D)
C
设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( )
通过这堂课的研究,你明确了 ,
你的收获与感受是 ,
你存在的疑惑之处有 。
(课本) P97 1,2
A
函数 y = f (x) 在给定区间 G 上,当 x 1、x 2 ∈G 且 x 1< x 2 时
y
x
o
a
b
y
x
o
a
b
1)都有 f ( x 1 ) < f ( x 2 ),
则 f ( x ) 在G 上是增函数;
2)都有 f ( x 1 ) > f ( x 2 ),
则 f ( x ) 在G 上是减函数;
若 f(x) 在G上是增函数或减函数,
则 f(x) 在G上具有严格的单调性。
G 称为单调区间
G = ( a , b )
定义法
图象法
判断函数单调性有哪些方法?
比如:判断函数 的单调性。
x
y
o
函数在 上为____函数,
在 上为____函数。
图象法
定义法
减
增
如图:
图象是单调上升的.
观察下列图象的单调区间,
并求单调区间相应的导数.
图象是单调下降的.
在x∈(-∞,0)内
图象是单调上升的.
在x∈( 0,+∞)内
图象是单调上升的.
图象是单调下降的.
在x∈(-∞,0)内
图象是单调下降的.
在x∈( 0,+∞)内
函数的单调性与其导函数正负的关系:
当函数y=f (x)在某个区间内可导时,
如果 , 则f (x)为增函数;
如果 , 则f (x)为减函数。
动态
演示
单调性
导数的正负
函数及图象
x
y
o
x
y
o
切线斜率
的正负
x
y
o
k>0
k>0
k<0
k<0
+
+
-
-
递增
递减
注意:
应正确理解 “ 某个区间 ” 的含义, 它必是定义域内的某个区间。
如果在某个区间内恒有 =0 ,则f(x)为常数函数.
例1、已知导函数 的下列信息:
当1
当x>4,或x<1时, <0
当x=4,或x=1时, =0
试画出函数f(x)图象的大致形状。
4
1
解:由题意可知
当1
当x>4,或x<1时,
f(x)为减函数
当x=4,或x=1时,
两点为“临界点”
其图象的大致形状如图。
例2、判断下列函数的单调性,并求出
单调区间:
(1) f(x)=x3+3x ;
解: =3x2+3=3(x2+1)>0
从而函数f(x)=x3+3x
在x∈R上单调递增,
见右图。
(2) f(x)=x2-2x-3 ;
解: =2x-2=2(x-1)>0
图象见右图。
当 >0,即x>1时,函数单调递增;
当 <0,即x<1时,
函数单调递减;
(3) f(x)=sinx-x ; x∈(0,p)
解: =cosx-1<0
从而函数f(x)=sinx-x
在x∈(0, )单调递减,
见右图。
(4) f(x)=2x3+3x2-24x+1 ;
解: =6x2+6x-24=6(x2+x-4)>0
当 >0,
即 时,
函数单调递增;
图象见右图。
当 <0,
即 时,
函数单调递减;
例3 如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.
(A)
(B)
(C)
(D)
h
t
O
h
t
O
h
t
O
h
t
O
(1)
(2)
(3)
(4)
(1)→(B),(2)→(A),(3)→(D),(4)→(C)
总结: 当遇到三次或三次以上的,或图象很难
画出的函数求单调性问题时,应考虑导数法。
①求定义域
②求
③令
④做出结论
1°什么情况下,用“导数法” 求函数单调性、
单调区间较简便?
2°试总结用“导数法” 求单调区间的步骤?
(04年全国理)
B
x
y
o
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
2
(A)
(B)
(C)
(D)
C
设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( )
通过这堂课的研究,你明确了 ,
你的收获与感受是 ,
你存在的疑惑之处有 。
(课本) P97 1,2
A
