5.3.1函数的单调性 课件(共58张PPT)
文档属性
| 名称 | 5.3.1函数的单调性 课件(共58张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 08:52:10 | ||
图片预览









文档简介
(共58张PPT)
1.函数f(x)的单调性与导函数f(x)正负之间的关系
在某个区间(a,b)上的函数y=f(x):
(x)的正负
f(x)的单调性
f(x)>0
函数f(x)在(a,b)上单调递增
f(x)<0
函数f(x)在(a,b)上单调递减
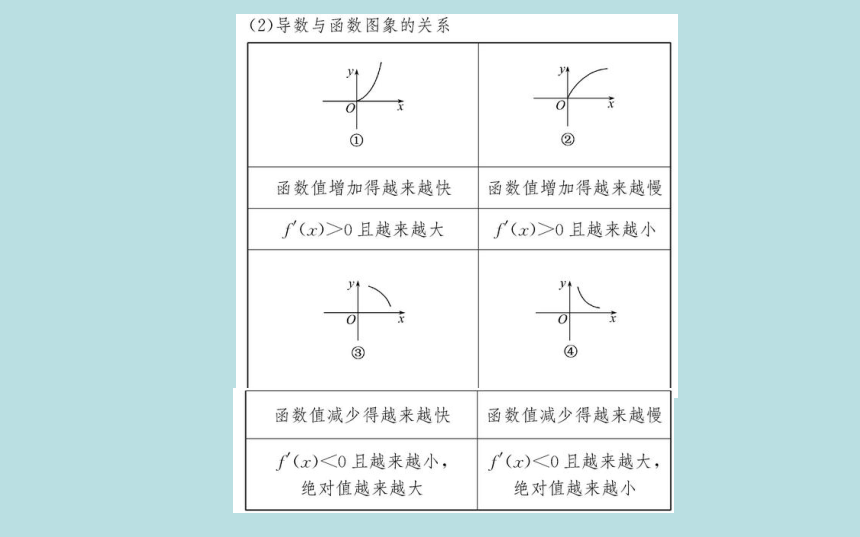
2.函数图象的变化趋势与导数值大小的关系
一个函数f(x)在某一范围内导数的绝对值为f(x)|,则
If()
函数值的变化
函数的图象
比较“陡峭”
越大
在这一范围内变化得较快
(向上或向下)
越小
在这一范围内变化得较慢
比较“平缓”
之素养小测
1.思维辨析(对的打“、/”,错的打“×”)
(1)因为()/=-之<0恒成立,所以函数y=
(一∞,十∞)上单调递减,
(2)因为(x-)=1+是>0,所以函数y=x-在
(一∞,十∞)上单调递增,
(3)函数f(x)=x2+2x一3的导数f(x)=2x+2是增
函数,所以函数f(x)=x2+2x一3在(一∞,十∞)上是
提示:(1)X.因为函数y=的定义域为(-∞,0)U(0,
+∞),)/=-是<0恒成立,
所以函数y=二在(-∞,0)和(0,十∞)上单调递减.
(2)X.因为函数y=x-1的定义域为(-∞,0)U(0,
十∞),由(x-)/=1+之>0恒成立,所以函数y=x
-1在(-∞,0)和(0,十∞)上单调递增.
类型一导数与函数图象的关系
【典例1】(1)已知函数y=f(x)的图象是下列
四个图象之一,且其导函数y-f(x)的图
象如图所示,则该函数的图象是
A
D
A.
B.
D.
y=fx)
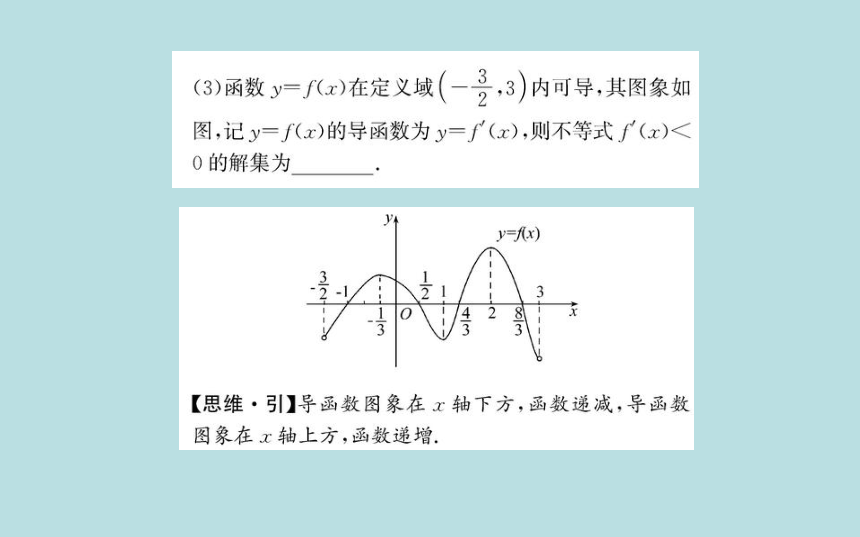
【思维·引】导函数图象在x轴下方,函数递减,导函数
图象在x轴上方,函数递增
【解析】(1)选B.在区间(一1,1)上,f(x)>0,因此函数
y=f(x)在区间(一1,1)上为增函数,易知四个选项都符
合.在区间(一1,0)上,f(x)单调递增,故y=f(x)在区
间(一1,0)上增加得越来越快,函数图象应为指数增长
的模式;在区间(0,1)上,f(x)单调递减,故y=(x)在
区间(0,1)上增加得越来越慢,函数图象应为对数增长
的模式
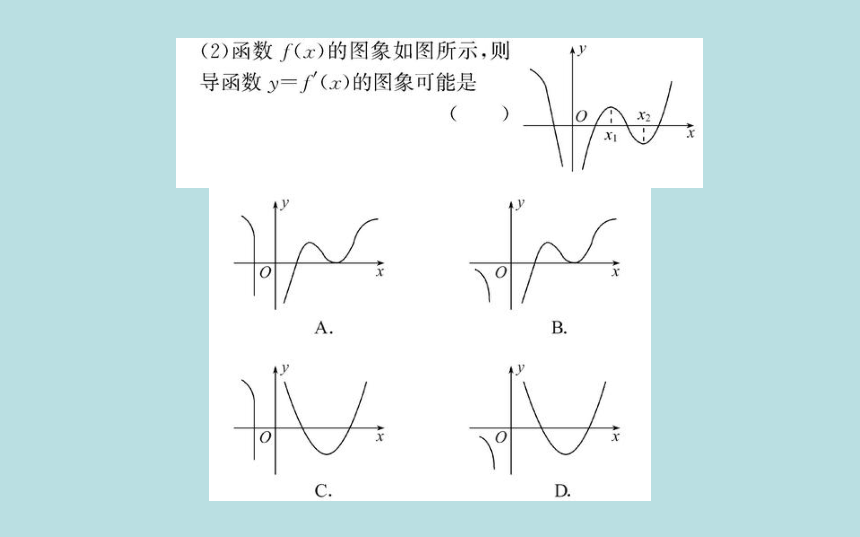
(2)选D.从函数y=f(x)的图象可以看出,其在区间
(一∞,0)上是减函数,f(x)<0;在区间(0,x1)上是增
函数,f(x)>0;在区间(x1,x2)上是减函数,f(x)<0;
在区间(x2,十∞)上是增函数,f(x)>0.结合选项可
知,只有D项满足
1.函数f(x)的单调性与导函数f(x)正负之间的关系
在某个区间(a,b)上的函数y=f(x):
(x)的正负
f(x)的单调性
f(x)>0
函数f(x)在(a,b)上单调递增
f(x)<0
函数f(x)在(a,b)上单调递减
2.函数图象的变化趋势与导数值大小的关系
一个函数f(x)在某一范围内导数的绝对值为f(x)|,则
If()
函数值的变化
函数的图象
比较“陡峭”
越大
在这一范围内变化得较快
(向上或向下)
越小
在这一范围内变化得较慢
比较“平缓”
之素养小测
1.思维辨析(对的打“、/”,错的打“×”)
(1)因为()/=-之<0恒成立,所以函数y=
(一∞,十∞)上单调递减,
(2)因为(x-)=1+是>0,所以函数y=x-在
(一∞,十∞)上单调递增,
(3)函数f(x)=x2+2x一3的导数f(x)=2x+2是增
函数,所以函数f(x)=x2+2x一3在(一∞,十∞)上是
提示:(1)X.因为函数y=的定义域为(-∞,0)U(0,
+∞),)/=-是<0恒成立,
所以函数y=二在(-∞,0)和(0,十∞)上单调递减.
(2)X.因为函数y=x-1的定义域为(-∞,0)U(0,
十∞),由(x-)/=1+之>0恒成立,所以函数y=x
-1在(-∞,0)和(0,十∞)上单调递增.
类型一导数与函数图象的关系
【典例1】(1)已知函数y=f(x)的图象是下列
四个图象之一,且其导函数y-f(x)的图
象如图所示,则该函数的图象是
A
D
A.
B.
D.
y=fx)
【思维·引】导函数图象在x轴下方,函数递减,导函数
图象在x轴上方,函数递增
【解析】(1)选B.在区间(一1,1)上,f(x)>0,因此函数
y=f(x)在区间(一1,1)上为增函数,易知四个选项都符
合.在区间(一1,0)上,f(x)单调递增,故y=f(x)在区
间(一1,0)上增加得越来越快,函数图象应为指数增长
的模式;在区间(0,1)上,f(x)单调递减,故y=(x)在
区间(0,1)上增加得越来越慢,函数图象应为对数增长
的模式
(2)选D.从函数y=f(x)的图象可以看出,其在区间
(一∞,0)上是减函数,f(x)<0;在区间(0,x1)上是增
函数,f(x)>0;在区间(x1,x2)上是减函数,f(x)<0;
在区间(x2,十∞)上是增函数,f(x)>0.结合选项可
知,只有D项满足
