5.1.2 导数的几何意义 第2课时 课件(共26张PPT)
文档属性
| 名称 | 5.1.2 导数的几何意义 第2课时 课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 09:00:52 | ||
图片预览






文档简介
(共26张PPT)
导数的几何意义
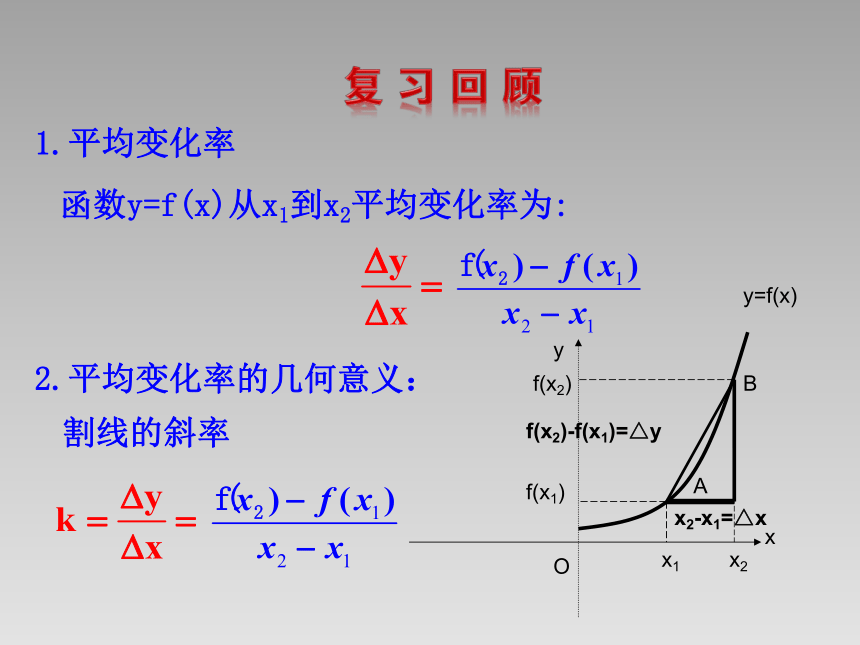
1.平均变化率
函数y=f(x)从x1到x2平均变化率为:
2.平均变化率的几何意义:
O
A
B
x
y
y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
割线的斜率
3.导数的概念
函数 y = f (x) 在 x = x0 处的瞬时变化率
称为函数 y = f (x) 在 x = x0 处的导数, 记作
或 , 即
4.求函数y=f(x)在x=x0处的导数的一般步骤是:
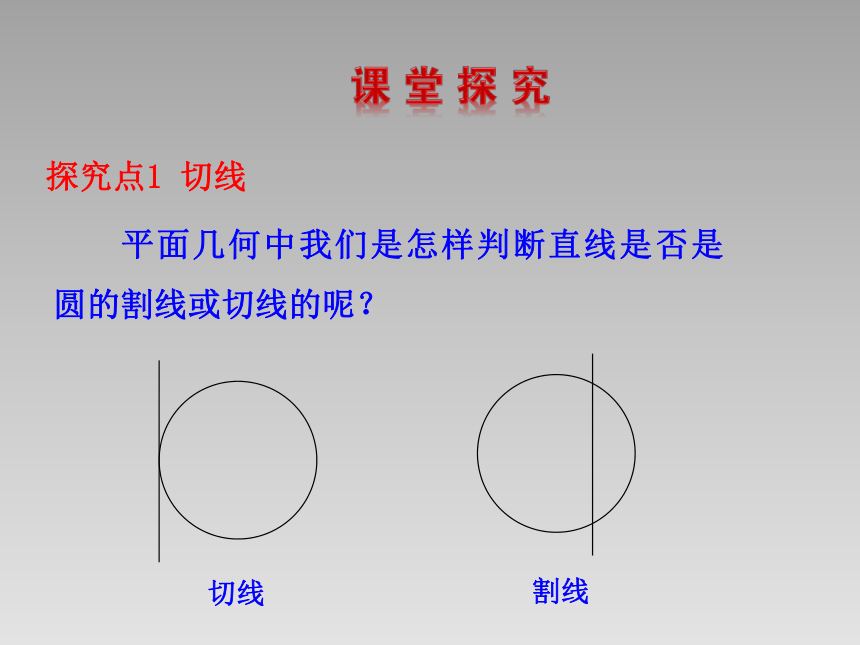
平面几何中我们是怎样判断直线是否是圆的割线或切线的呢?
探究点1 切线
切线
割线
如图直线l1是曲线C的切线吗 l2呢
l2
l1
A
B
0
x
y
l1不是曲线C的切线,l2是曲线C的切线.
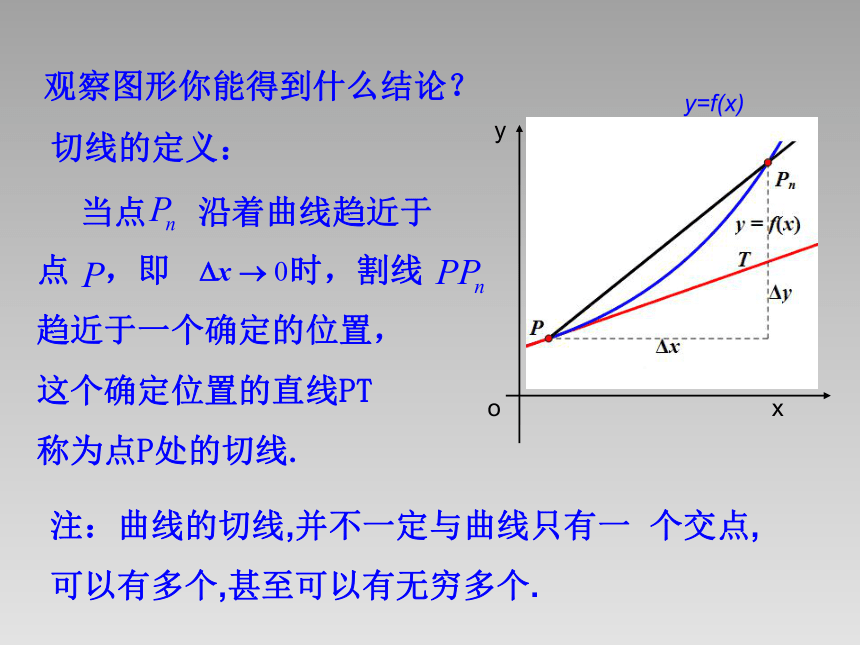
观察图形你能得到什么结论?
切线的定义:
当点 沿着曲线趋近于
点 ,即 时,割线
趋近于一个确定的位置,
这个确定位置的直线PT
称为点P处的切线.
注:曲线的切线,并不一定与曲线只有一 个交点,
可以有多个,甚至可以有无穷多个.
x
y
o
y=f(x)
在上面的研究过程中,某点的割线斜率和切线
斜率与某点附近的平均变化率和某点的瞬时变化率
有何联系?
平均变化率
割线的斜率
瞬时变化率(导数)
切线的斜率
探究点2 导数的几何意义
函数 在 处的导数就是曲线
在点(x0,f(x0))处的切线的斜率 , 即:
曲线在点(x0,f(x0))处的切线的方程为:
导数的几何意义
例1 求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.
Q
P
y
=
x
2
+1
x
y
-
1
1
1
O
j
M
D
y
D
x
因此,切线方程为y-2=2(x-1),
即y=2x.
解:
【总结提升】
求曲线在某点处的切线方程的基本步骤:
①求出切点P的坐标;
②求切线的斜率,即函数y=f(x)在x=x0处的导数;
③利用点斜式求切线方程.
例2 如图, 它表示跳水运动中高度随时间变化的函数
的图象. 根据图象, 请描述、
比较曲线 在 附近的变化情况.
t
o
h
t0
t1
t2
l0
l1
l2
t4
t3
解:可用曲线 h(t) 在t0 , t1 , t2处的切线刻画曲线h(t)在上述三个时刻附近的变化情况.
(1)当t = t0时, 曲线 h(t) 在
t0 处的切线 l0 平行于 t 轴.
故在t = t0 附近曲线比较平坦, 几乎没有升降.
t
o
h
l0
t0
t1
l1
t2
l2
t4
t3
(2)当 t = t1 时, 曲线 h(t) 在 t1 处的切线 l1 的斜率 h (t1) <0 .故在t = t1 附近曲线下降,即函数 h(t) 在 t = t1 附近单调递减.
t
o
h
l0
t0
t1
l1
t2
l2
t4
t3
从图可以看出,直线 l1 的倾斜程度小于直线 l2 的倾斜程度,这说明曲线h(t) 在 t1 附近比在t2 附近下降得缓慢.
(3)当 t = t2 时, 曲线 h(t) 在 t2处的切线 l2 的斜率 h (t2) <0 .故在 t = t2 附近曲线下降,即函数 h(t) 在t = t2 附近也单调递减.
【总结提升】
通过观察跳水问题中导数的变化情况,你得到了哪些结论
(1)以直代曲:大多数函数就一小段范围看,大致
可以看作直线,某点附近的曲线可以用过该点的
切线近似代替;
(2)函数的单调性与其导函数正负的关系;
(3)曲线的变化快慢及切线的倾斜角的内在联系.
例3 如图表示人体血管中的药物浓度c=f(t)(单位:mg/ml)随时间t(单位:min)变化的函数图象,根据图象,估计 t=0.2,0.4,0.6,0.8 min时,血管中 药物浓度的瞬时变化率,把数据用表格的形式列出。(精确到0.1)
解:血管中药物浓度的瞬时变化率,
就是药物浓度
从图象上看,它表示曲线在该点处的切线的斜率.
函数f(t)在此时刻的导数,
(数形结合,以直代曲)
以简单对象刻画复杂的对象
t 0.2 0.4 0.6 0.8
药物浓度的
瞬时变化率
0.4
- 0.7
一、选择题
1.曲线y=-2x2+1在点(0,1)处的切线的斜率是
( )
A.-4 B.0
C.4 D.不存在
B
B
3.若曲线y=h(x)在点P(a,h(a))处的切线方程为2x+y+1=0,那么 ( )
A.h′(a)=0 B.h′(a)<0
C.h′(a)>0 D.h′(a)不确定
B
4.曲线y=x3在点P处的切线斜率为3,则点P的坐标为 ( )
A.(-2,-8) B.(1,1),(-1,-1)
C. ( 2 , 8) D.
B
y=2x-1
2.函数 在 处的导数 的几何意义,就是函数 的图象在点 处的切线的斜率(数形结合)
=切线 的斜率k
1.曲线的切线定义
4.导函数(简称导数)
3.利用导数的几何意义解释实际生活问题,体会
“数形结合”,“以直代曲”的数学思想方法.
以简单对象刻画复杂的对象
导数的几何意义
1.平均变化率
函数y=f(x)从x1到x2平均变化率为:
2.平均变化率的几何意义:
O
A
B
x
y
y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
割线的斜率
3.导数的概念
函数 y = f (x) 在 x = x0 处的瞬时变化率
称为函数 y = f (x) 在 x = x0 处的导数, 记作
或 , 即
4.求函数y=f(x)在x=x0处的导数的一般步骤是:
平面几何中我们是怎样判断直线是否是圆的割线或切线的呢?
探究点1 切线
切线
割线
如图直线l1是曲线C的切线吗 l2呢
l2
l1
A
B
0
x
y
l1不是曲线C的切线,l2是曲线C的切线.
观察图形你能得到什么结论?
切线的定义:
当点 沿着曲线趋近于
点 ,即 时,割线
趋近于一个确定的位置,
这个确定位置的直线PT
称为点P处的切线.
注:曲线的切线,并不一定与曲线只有一 个交点,
可以有多个,甚至可以有无穷多个.
x
y
o
y=f(x)
在上面的研究过程中,某点的割线斜率和切线
斜率与某点附近的平均变化率和某点的瞬时变化率
有何联系?
平均变化率
割线的斜率
瞬时变化率(导数)
切线的斜率
探究点2 导数的几何意义
函数 在 处的导数就是曲线
在点(x0,f(x0))处的切线的斜率 , 即:
曲线在点(x0,f(x0))处的切线的方程为:
导数的几何意义
例1 求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.
Q
P
y
=
x
2
+1
x
y
-
1
1
1
O
j
M
D
y
D
x
因此,切线方程为y-2=2(x-1),
即y=2x.
解:
【总结提升】
求曲线在某点处的切线方程的基本步骤:
①求出切点P的坐标;
②求切线的斜率,即函数y=f(x)在x=x0处的导数;
③利用点斜式求切线方程.
例2 如图, 它表示跳水运动中高度随时间变化的函数
的图象. 根据图象, 请描述、
比较曲线 在 附近的变化情况.
t
o
h
t0
t1
t2
l0
l1
l2
t4
t3
解:可用曲线 h(t) 在t0 , t1 , t2处的切线刻画曲线h(t)在上述三个时刻附近的变化情况.
(1)当t = t0时, 曲线 h(t) 在
t0 处的切线 l0 平行于 t 轴.
故在t = t0 附近曲线比较平坦, 几乎没有升降.
t
o
h
l0
t0
t1
l1
t2
l2
t4
t3
(2)当 t = t1 时, 曲线 h(t) 在 t1 处的切线 l1 的斜率 h (t1) <0 .故在t = t1 附近曲线下降,即函数 h(t) 在 t = t1 附近单调递减.
t
o
h
l0
t0
t1
l1
t2
l2
t4
t3
从图可以看出,直线 l1 的倾斜程度小于直线 l2 的倾斜程度,这说明曲线h(t) 在 t1 附近比在t2 附近下降得缓慢.
(3)当 t = t2 时, 曲线 h(t) 在 t2处的切线 l2 的斜率 h (t2) <0 .故在 t = t2 附近曲线下降,即函数 h(t) 在t = t2 附近也单调递减.
【总结提升】
通过观察跳水问题中导数的变化情况,你得到了哪些结论
(1)以直代曲:大多数函数就一小段范围看,大致
可以看作直线,某点附近的曲线可以用过该点的
切线近似代替;
(2)函数的单调性与其导函数正负的关系;
(3)曲线的变化快慢及切线的倾斜角的内在联系.
例3 如图表示人体血管中的药物浓度c=f(t)(单位:mg/ml)随时间t(单位:min)变化的函数图象,根据图象,估计 t=0.2,0.4,0.6,0.8 min时,血管中 药物浓度的瞬时变化率,把数据用表格的形式列出。(精确到0.1)
解:血管中药物浓度的瞬时变化率,
就是药物浓度
从图象上看,它表示曲线在该点处的切线的斜率.
函数f(t)在此时刻的导数,
(数形结合,以直代曲)
以简单对象刻画复杂的对象
t 0.2 0.4 0.6 0.8
药物浓度的
瞬时变化率
0.4
- 0.7
一、选择题
1.曲线y=-2x2+1在点(0,1)处的切线的斜率是
( )
A.-4 B.0
C.4 D.不存在
B
B
3.若曲线y=h(x)在点P(a,h(a))处的切线方程为2x+y+1=0,那么 ( )
A.h′(a)=0 B.h′(a)<0
C.h′(a)>0 D.h′(a)不确定
B
4.曲线y=x3在点P处的切线斜率为3,则点P的坐标为 ( )
A.(-2,-8) B.(1,1),(-1,-1)
C. ( 2 , 8) D.
B
y=2x-1
2.函数 在 处的导数 的几何意义,就是函数 的图象在点 处的切线的斜率(数形结合)
=切线 的斜率k
1.曲线的切线定义
4.导函数(简称导数)
3.利用导数的几何意义解释实际生活问题,体会
“数形结合”,“以直代曲”的数学思想方法.
以简单对象刻画复杂的对象
