5.1函数的单调性与导数(共22张PPT)
文档属性
| 名称 | 5.1函数的单调性与导数(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 19:31:35 | ||
图片预览





文档简介
(共22张PPT)
导数在研究函数中的应用
函数的单调性与导数
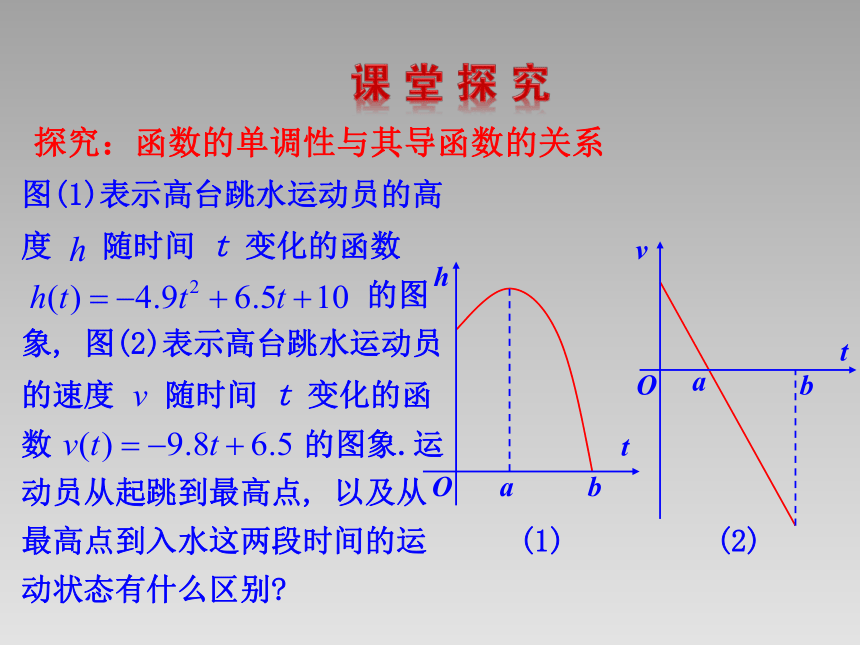
图(1)表示高台跳水运动员的高
度 随时间 t 变化的函数
的图
象, 图(2)表示高台跳水运动员
的速度 随时间 t 变化的函
数 的图象.运
动员从起跳到最高点, 以及从
最高点到入水这两段时间的运
动状态有什么区别
a
a
b
b
t
t
v
h
O
O
(1)
(2)
探究:函数的单调性与其导函数的关系
a
a
b
b
t
t
v
h
O
O
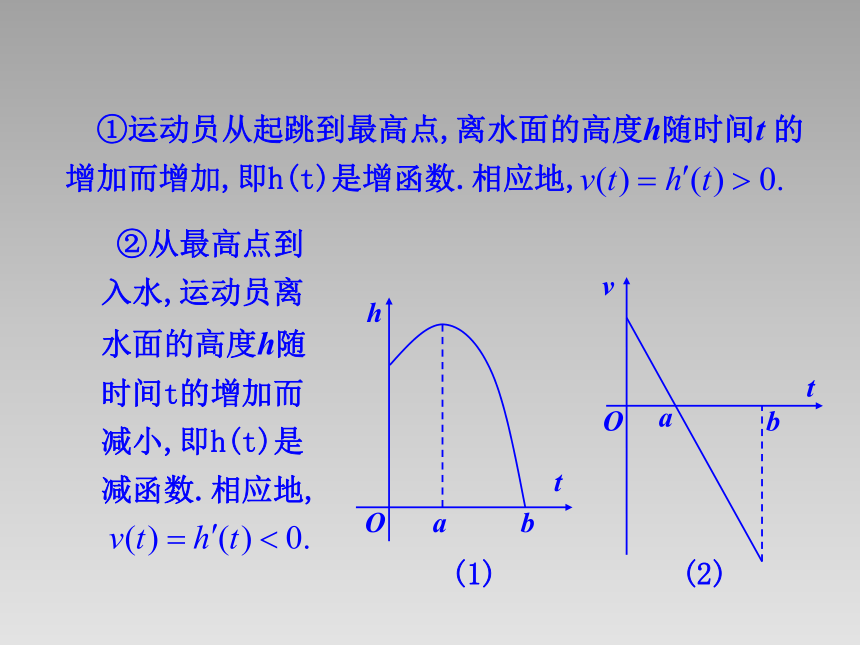
①运动员从起跳到最高点,离水面的高度h随时间t 的增加而增加,即h(t)是增函数.相应地,
②从最高点到入水,运动员离水面的高度h随时间t的增加而减小,即h(t)是减函数.相应地,
(1)
(2)
O
O
O
O
例1 已知导函数 的下列信息:
当1 < x < 4 时,
当 x > 4 , 或 x < 1时,
当 x = 4 , 或 x = 1时,
试画出函数f(x)图象的大致形状.
解:
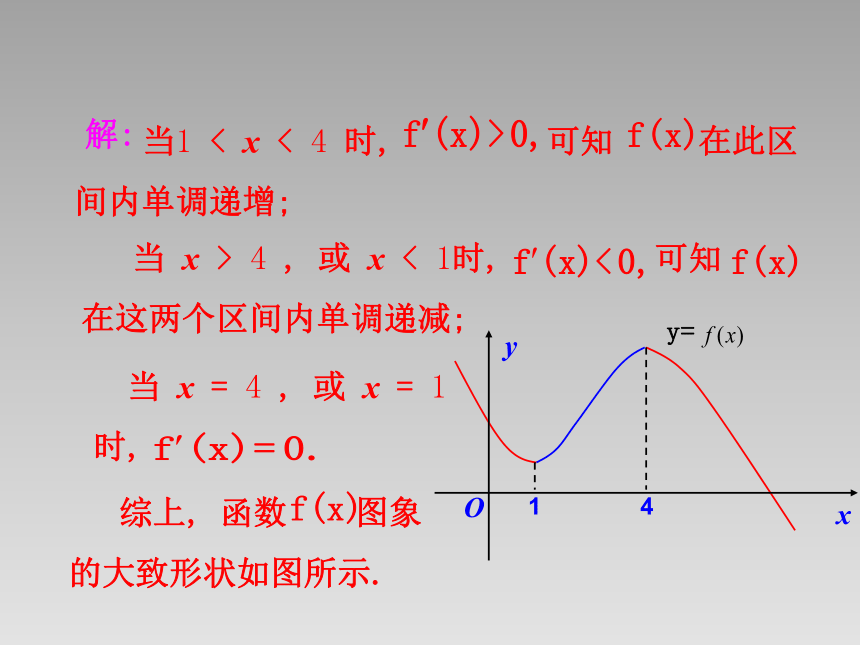
当1 < x < 4 时, 可知 在此区间内单调递增;
当 x > 4 , 或 x < 1时, 可知 在这两个区间内单调递减;
当 x = 4 , 或 x = 1时,
综上, 函数 图象的大致形状如图所示.
x
y
O
1
4
y=
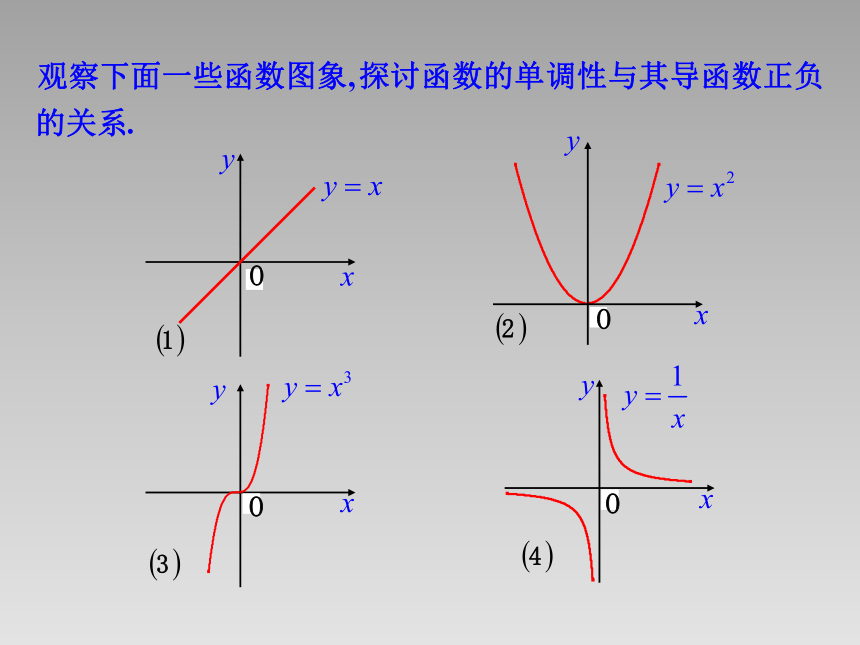
例2 判断下列函数的单调性, 并求出单调区间:
解:
(1) 因为 , 所以
因此, 函数 在
上单调递增.如图(1)所示
单调递减
单调递增
单调递减
根据导数确定函数的单调性步骤:
1.确定函数f(x)的定义域.
2.求出函数的导数.
3.解不等式f (x)>0,得函数单调增区间;
解不等式f (x)<0,得函数单调减区间.
总结提升
1.函数y=3x-x3的单调增区间是( )
A. (0,+∞) B. (-∞,-1)
C. (-1,1) D. (1,+∞)
C
2.设f(x)=x+ (x<0),则f(x)的单调增区间是
( )
A. (-∞,-2)
B. (-2,0)
C. (-∞,- )
D. (- ,0)
C
3.函数y=xlnx在区间(0,1)上是 ( )
A.单调增函数
B.单调减函数
C. 在(0, )上是减函数,在( , 1)上是
增函数
D. 在( , 1)上是减函数,在(0, )上是
增函数
C
4.函数y=x2(x+3)的单调递减区间是 ,
单调递增区间是 .
(-2,0)
(-∞,-2)及(0,+∞)
5.函数f(x)=cos2x的单调递减区间是
.
(kπ, kπ+ ), k∈Z
1.求可导函数f(x)单调区间的步骤:
(1)求
(2)解不等式 >0(或 <0)
(3)确认并指出递增区间(或递减区间)
2.证明可导函数f(x)在(a,b)内的单调性的方法:
(1)求
(2)确认 在(a,b)内的符号
(3)作出结论
导数在研究函数中的应用
函数的单调性与导数
图(1)表示高台跳水运动员的高
度 随时间 t 变化的函数
的图
象, 图(2)表示高台跳水运动员
的速度 随时间 t 变化的函
数 的图象.运
动员从起跳到最高点, 以及从
最高点到入水这两段时间的运
动状态有什么区别
a
a
b
b
t
t
v
h
O
O
(1)
(2)
探究:函数的单调性与其导函数的关系
a
a
b
b
t
t
v
h
O
O
①运动员从起跳到最高点,离水面的高度h随时间t 的增加而增加,即h(t)是增函数.相应地,
②从最高点到入水,运动员离水面的高度h随时间t的增加而减小,即h(t)是减函数.相应地,
(1)
(2)
O
O
O
O
例1 已知导函数 的下列信息:
当1 < x < 4 时,
当 x > 4 , 或 x < 1时,
当 x = 4 , 或 x = 1时,
试画出函数f(x)图象的大致形状.
解:
当1 < x < 4 时, 可知 在此区间内单调递增;
当 x > 4 , 或 x < 1时, 可知 在这两个区间内单调递减;
当 x = 4 , 或 x = 1时,
综上, 函数 图象的大致形状如图所示.
x
y
O
1
4
y=
例2 判断下列函数的单调性, 并求出单调区间:
解:
(1) 因为 , 所以
因此, 函数 在
上单调递增.如图(1)所示
单调递减
单调递增
单调递减
根据导数确定函数的单调性步骤:
1.确定函数f(x)的定义域.
2.求出函数的导数.
3.解不等式f (x)>0,得函数单调增区间;
解不等式f (x)<0,得函数单调减区间.
总结提升
1.函数y=3x-x3的单调增区间是( )
A. (0,+∞) B. (-∞,-1)
C. (-1,1) D. (1,+∞)
C
2.设f(x)=x+ (x<0),则f(x)的单调增区间是
( )
A. (-∞,-2)
B. (-2,0)
C. (-∞,- )
D. (- ,0)
C
3.函数y=xlnx在区间(0,1)上是 ( )
A.单调增函数
B.单调减函数
C. 在(0, )上是减函数,在( , 1)上是
增函数
D. 在( , 1)上是减函数,在(0, )上是
增函数
C
4.函数y=x2(x+3)的单调递减区间是 ,
单调递增区间是 .
(-2,0)
(-∞,-2)及(0,+∞)
5.函数f(x)=cos2x的单调递减区间是
.
(kπ, kπ+ ), k∈Z
1.求可导函数f(x)单调区间的步骤:
(1)求
(2)解不等式 >0(或 <0)
(3)确认并指出递增区间(或递减区间)
2.证明可导函数f(x)在(a,b)内的单调性的方法:
(1)求
(2)确认 在(a,b)内的符号
(3)作出结论
