5.1.1变化率问题 课件(共16张PPT)
文档属性
| 名称 | 5.1.1变化率问题 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 09:01:35 | ||
图片预览






文档简介
(共16张PPT)
1.瞬时速度
我们把物体在某一时刻的速度称为瞬时速度.
2.极限
对于-h十)-hC1=一4.9△-5,我们把-5叫
(1+△t)-1
做“当△无限趋近于0时,0=h1+)一h的极
△t
限”,记为li
h(1+△t)-h(1)
-5.
△*0
△t
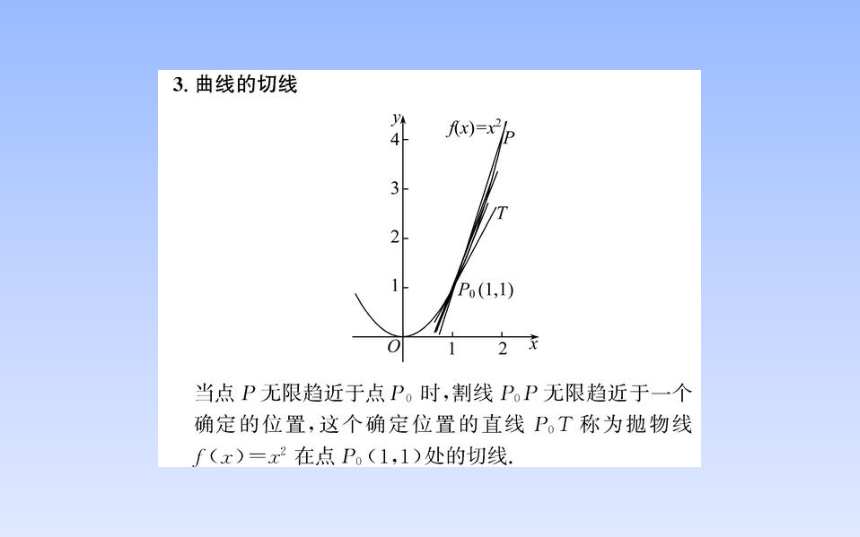
3.曲线的切线
fx)=x'lp
Po(1,1)
2
当点P无限趋近于点P。时,割线P。P无限趋近于一个
确定的位置,这个确定位置的直线P。T称为抛物线
f(x)=x2在点P。(1,1)处的切线.
2.某物体的位移公式为s=s(t),从t。到to+△t这段时间
内下列理解正确的是
A.(to十△t)一to称为函数值增量
B.to称为函数值增量
C.△s=s(to十△t)一s(to)称为函数值增量
会称为函数值增量
D.
【解析】选C.由自变量的变化量、函数值的变化量、平均
变化率的概念易得C正确.
S2
甲
S1
to
A.在0到to范围内甲的平均速度大于乙的平均速度
B.在0到to范围内甲的平均速度小于乙的平均速度
C.在t到t1范围内甲的平均速度大于乙的平均速度
类型二求瞬时速度
【典例2】(1)质点M按规律s=2t+3做直线运动(位移单
位:m,时间单位:s),则质点M在t=2s时的瞬时速度
是
A.2 m/s
B.6 m/s
C.4 m/s
D.8 m/s
(2)一质点运动的方程为s=5一3t,若该质点在t=1
到t=1+△t这段时间内的平均速度为一3△t一6,则该
质点在t=1时的瞬时速度是
A.-3
B.3
C.6
D.-6
【思维·引】关键是求位移改变量
【解析(1)选D.o=im
(2+△t)2+3-(2×22+3)
△y*0
△t
-lim
△1*0
8+2(△)2=lim(8+2△r)=8(m/s).
△t
△0
(2)选D.v=lim(-3△t-6)=-6.
△*0
2.已知函数y=ax2+b在点(1,3)处的切线斜率为2,则。=
【解析】li
a(1+△x)2+b-(a+b
2=lim(2a+a△x)=
△x0
△x
△0
2a=2,
解得a=1,把切,点(1,3)代入函数y=a.x2十b,
得3=a十b,所以b=3-a=2,故b=2.
答案:2
角度2求切点坐标
【典例4】已知曲线y=2x2一7在点P处的切线方程为8x
一y一15=0,则切点P的坐标为
A.(-2,1)
B.(0,-7)
C.(2,1)
D.(3,11)
【思维·引】求出切点的横坐标,进而求出切点坐标
【解析】选C.设P点坐标为(xo,2x一7),
则lim
f(xo+△x)-f(xo)
△x0
△x
lim
2[x6+2xo△x+(△x)2]-7-2x号+7
△x*0
△x
=lim(4xo+2△x)=4xo.
所以4xo=8,解得xo=2.
所以P的坐标为(2,1).
1.瞬时速度
我们把物体在某一时刻的速度称为瞬时速度.
2.极限
对于-h十)-hC1=一4.9△-5,我们把-5叫
(1+△t)-1
做“当△无限趋近于0时,0=h1+)一h的极
△t
限”,记为li
h(1+△t)-h(1)
-5.
△*0
△t
3.曲线的切线
fx)=x'lp
Po(1,1)
2
当点P无限趋近于点P。时,割线P。P无限趋近于一个
确定的位置,这个确定位置的直线P。T称为抛物线
f(x)=x2在点P。(1,1)处的切线.
2.某物体的位移公式为s=s(t),从t。到to+△t这段时间
内下列理解正确的是
A.(to十△t)一to称为函数值增量
B.to称为函数值增量
C.△s=s(to十△t)一s(to)称为函数值增量
会称为函数值增量
D.
【解析】选C.由自变量的变化量、函数值的变化量、平均
变化率的概念易得C正确.
S2
甲
S1
to
A.在0到to范围内甲的平均速度大于乙的平均速度
B.在0到to范围内甲的平均速度小于乙的平均速度
C.在t到t1范围内甲的平均速度大于乙的平均速度
类型二求瞬时速度
【典例2】(1)质点M按规律s=2t+3做直线运动(位移单
位:m,时间单位:s),则质点M在t=2s时的瞬时速度
是
A.2 m/s
B.6 m/s
C.4 m/s
D.8 m/s
(2)一质点运动的方程为s=5一3t,若该质点在t=1
到t=1+△t这段时间内的平均速度为一3△t一6,则该
质点在t=1时的瞬时速度是
A.-3
B.3
C.6
D.-6
【思维·引】关键是求位移改变量
【解析(1)选D.o=im
(2+△t)2+3-(2×22+3)
△y*0
△t
-lim
△1*0
8+2(△)2=lim(8+2△r)=8(m/s).
△t
△0
(2)选D.v=lim(-3△t-6)=-6.
△*0
2.已知函数y=ax2+b在点(1,3)处的切线斜率为2,则。=
【解析】li
a(1+△x)2+b-(a+b
2=lim(2a+a△x)=
△x0
△x
△0
2a=2,
解得a=1,把切,点(1,3)代入函数y=a.x2十b,
得3=a十b,所以b=3-a=2,故b=2.
答案:2
角度2求切点坐标
【典例4】已知曲线y=2x2一7在点P处的切线方程为8x
一y一15=0,则切点P的坐标为
A.(-2,1)
B.(0,-7)
C.(2,1)
D.(3,11)
【思维·引】求出切点的横坐标,进而求出切点坐标
【解析】选C.设P点坐标为(xo,2x一7),
则lim
f(xo+△x)-f(xo)
△x0
△x
lim
2[x6+2xo△x+(△x)2]-7-2x号+7
△x*0
△x
=lim(4xo+2△x)=4xo.
所以4xo=8,解得xo=2.
所以P的坐标为(2,1).
