北师大新版七年级(下)《第4章 三角形》单元测试卷(2)(含答案)
文档属性
| 名称 | 北师大新版七年级(下)《第4章 三角形》单元测试卷(2)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 367.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 10:30:39 | ||
图片预览


文档简介
北师大新版七年级(下)《第4章 三角形》单元测试卷(2)
一、选择题(共10小题)
1.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
2.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
3.如图,BP是△ABC中∠ABC的平分线,CP是△ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )
A.70° B.80° C.90° D.100°
4.如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
A.三边高的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三边中线的交点
5.如图,小明书上的三角形被墨迹遮挡了一部分,但他很快想到办法在作业本上画了一样的三角形,那么这两个三角形完全一样的依据是( )
A.AAS B.ASA C.SSS D.SAS
6.已知锐角三角形的边长是2,3,x,那么第三边x的取值范围是( )
A.1<x< B. C. D.
7.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
8.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是( )
A.m+n>b+c B.m+n<b+c C.m+n=b+c D.无法确定
9.如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为( )
A.27° B.59° C.69° D.79°
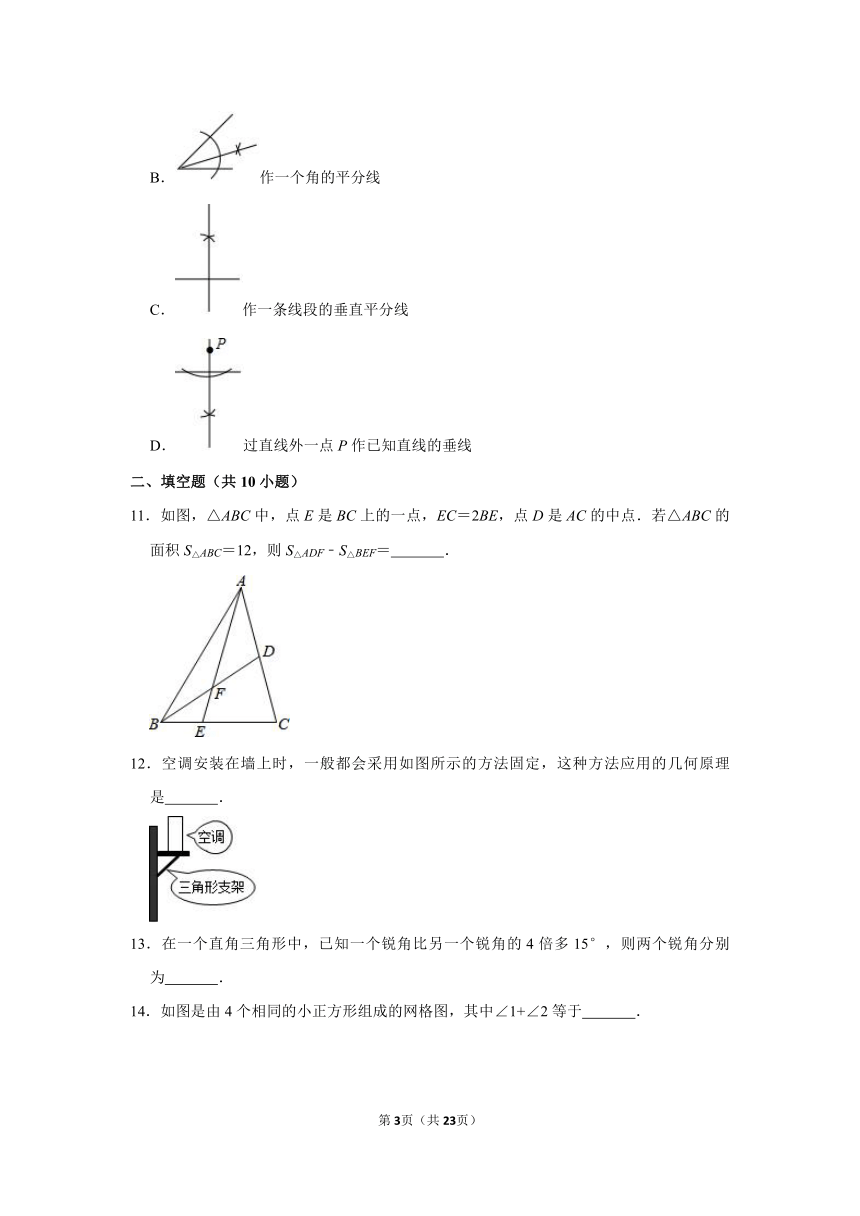
10.下列四种基本尺规作图分别表示,则对应选项中作法错误的是( )
A.作一个角等于已知角
B.作一个角的平分线
C.作一条线段的垂直平分线
D.过直线外一点P作已知直线的垂线
二、填空题(共10小题)
11.如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF﹣S△BEF= .
12.空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是 .
13.在一个直角三角形中,已知一个锐角比另一个锐角的4倍多15°,则两个锐角分别为 .
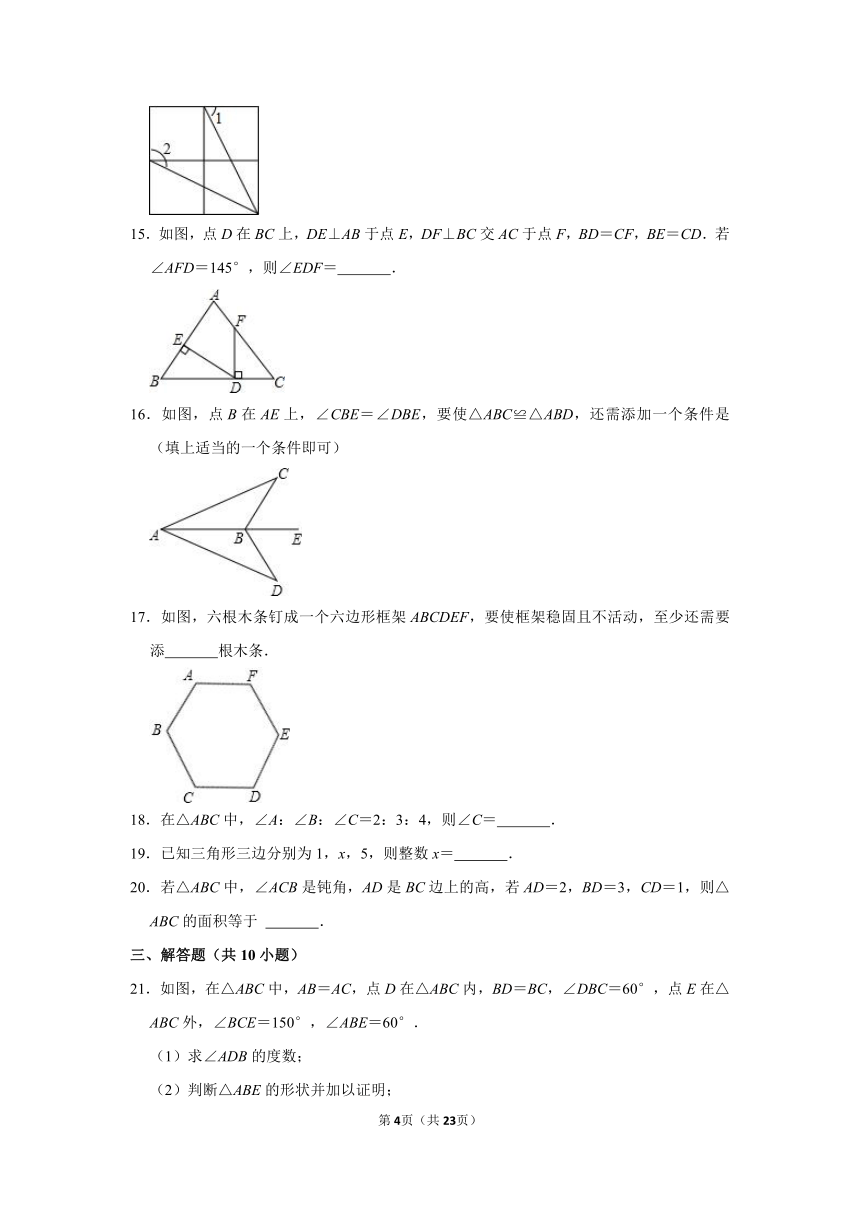
14.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于 .
15.如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF= .
16.如图,点B在AE上,∠CBE=∠DBE,要使△ABC≌△ABD,还需添加一个条件是 (填上适当的一个条件即可)
17.如图,六根木条钉成一个六边形框架ABCDEF,要使框架稳固且不活动,至少还需要添 根木条.
18.在△ABC中,∠A:∠B:∠C=2:3:4,则∠C= .
19.已知三角形三边分别为1,x,5,则整数x= .
20.若△ABC中,∠ACB是钝角,AD是BC边上的高,若AD=2,BD=3,CD=1,则△ABC的面积等于 .
三、解答题(共10小题)
21.如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.
(1)求∠ADB的度数;
(2)判断△ABE的形状并加以证明;
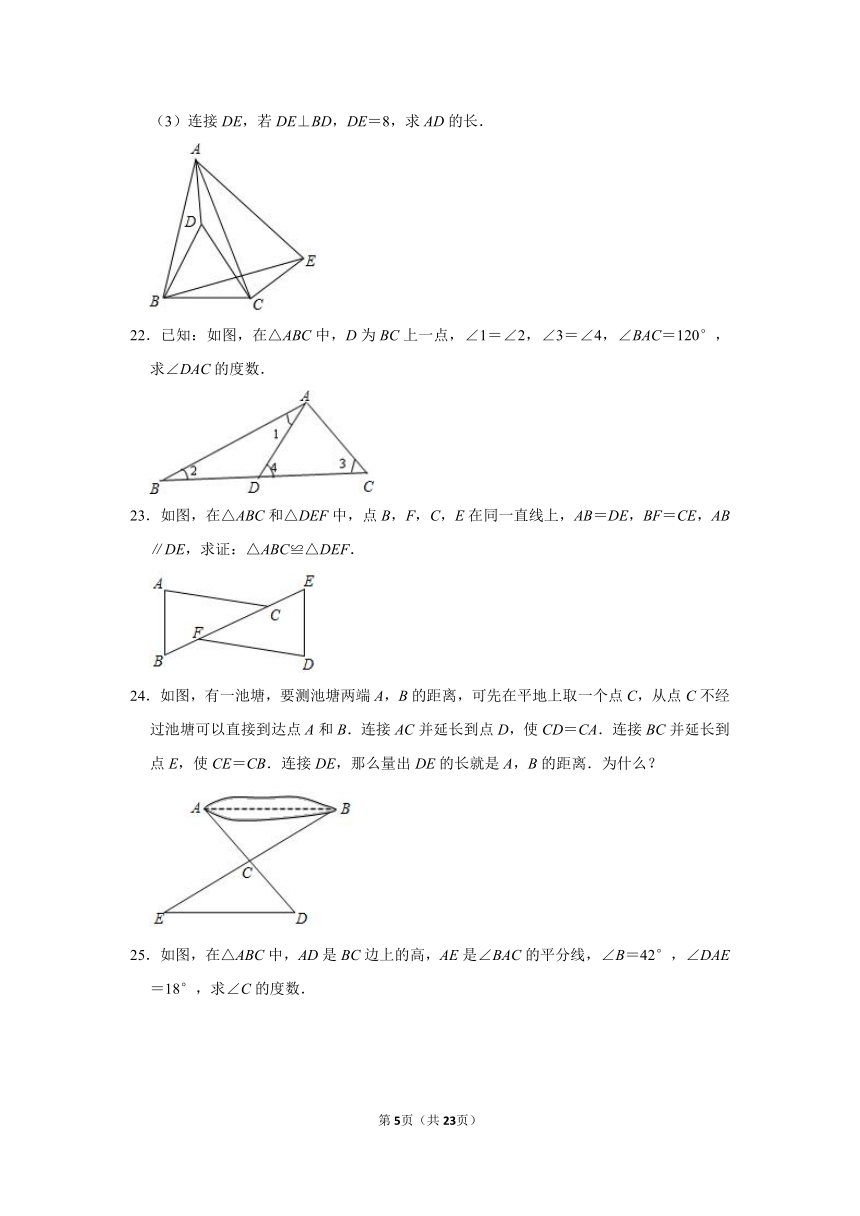
(3)连接DE,若DE⊥BD,DE=8,求AD的长.
22.已知:如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.
23.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,AB=DE,BF=CE,AB∥DE,求证:△ABC≌△DEF.
24.如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离.为什么?
25.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=42°,∠DAE=18°,求∠C的度数.
26.如图,点C是线段AB外一点,用没有刻度直尺和圆规画图:
(1)画射线CB;
(2)画直线AC;
(3)①延长线段AB到E,使AE=3AB;
②在①的条件下,如果AB=2cm,那么BE= cm.
27.如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC中边BC上的高AD;
(2)画出△ABC中边AC上的中线BE;
(3)直接写出△ABE的面积为 .
28.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BED=55°,求∠BAD的度数;
(2)作△BED的边BD边上的高;
(3)若△ABC的面积为20,BD=2.5,求△BDE中BD边上的高.
29.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
30.已知a、b、c为三角形三边的长,化简:|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|.
北师大新版七年级(下)《第4章 三角形》单元测试卷(2)
参考答案与试题解析
一、选择题(共10小题)
1.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
【解答】解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
2.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
【解答】解:∵AB=AC,∠BAE=∠CAD,
∴当添加AE=AD时,可根据“SAS”判断△ABE≌△ACD;
当添加∠B=∠C时,可根据“ASA”判断△ABE≌△ACD;
当添加∠AEB=∠ADC时,可根据“AAS”判断△ABE≌△ACD.
故选:C.
3.如图,BP是△ABC中∠ABC的平分线,CP是△ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )
A.70° B.80° C.90° D.100°
【解答】解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∵∠ABP=20°,∠ACP=50°,
∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,
∴∠A=∠ACM﹣∠ABC=60°,
∠ACB=180°﹣∠ACM=80°,
∴∠BCP=∠ACB+∠ACP=130°,
∵∠PBC=20°,
∴∠P=180°﹣∠PBC﹣∠BCP=30°,
∴∠A+∠P=90°,
故选:C.
4.如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
A.三边高的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三边中线的交点
【解答】解:∵支撑点应是三角形的重心,
∴三角形的重心是三角形三边中线的交点,
故选:D.
5.如图,小明书上的三角形被墨迹遮挡了一部分,但他很快想到办法在作业本上画了一样的三角形,那么这两个三角形完全一样的依据是( )
A.AAS B.ASA C.SSS D.SAS
【解答】解:由图可知,三角形两角及夹边可以作出,
所以,依据是ASA.
故选:B.
6.已知锐角三角形的边长是2,3,x,那么第三边x的取值范围是( )
A.1<x< B. C. D.
【解答】解:首先要能组成三角形,易得 1<x<5
下面求该三角形为直角三角形的边长情况(此为临界情况),显然长度为2的边对应的角必为锐角(2<3,短边对小角)则只要考虑3或者x为斜边的情况.
3为斜边时,由勾股定理,22+x2=32,得x=√5 作出图形,固定2边,旋转3边易知当1<x<√5 时,该三角形是以3为最大边的钝角三角形;
x 为斜边时,由勾股定理,22+32=x2,得x=√13,同样作图可得 当√13<x<5时,该三角形是以x为最大边的钝角三角形.
综上可知,当√5<x<√13 时,原三角形为锐角三角形.
故选:B.
7.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
【解答】解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,直角三角形沿虚线剪开即可得到一个直角三角形和一个钝角三角形.
因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.
综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.
故选:C.
8.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是( )
A.m+n>b+c B.m+n<b+c C.m+n=b+c D.无法确定
【解答】解:在BA的延长线上取点E,使AE=AC,连接EP,
∵AD是∠BAC的外角平分线,
∴∠CAD=∠EAD,
在△ACP和△AEP中,,
∴△ACP≌△AEP(SAS),
∴PE=PC,
在△PBE中,PB+PE>AB+AE,
∵PB=m,PC=n,AB=c,AC=b,
∴m+n>b+c.
故选:A.
9.如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为( )
A.27° B.59° C.69° D.79°
【解答】解如图,∵△ABC沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,
∴∠1=∠2,∠2=∠3,∠CDB=∠C′DB=74°,
∴∠1=∠2=∠3,
∴∠ABC=3∠3,
在△BCD中,∠3+∠C+∠CDB=180°,
∴∠3+∠C=180°﹣74°=106°,
在△ABC中,
∵∠A+∠ABC+∠C=180°,
∴20°+2∠3+(∠3+∠C)=180°,
即20°+2∠3+106°=180°,
∴∠3=27°,
∴∠C=106°﹣27°=79°,
故选:D.
10.下列四种基本尺规作图分别表示,则对应选项中作法错误的是( )
A.作一个角等于已知角
B.作一个角的平分线
C.作一条线段的垂直平分线
D.过直线外一点P作已知直线的垂线
【解答】解:①作一个角等于已知角的方法正确;
②作一个角的平分线的作法正确;
③作一条线段的垂直平分线缺少另一个交点,作法错误;
④过直线外一点P作已知直线的垂线的作法正确.
故选:C.
二、填空题(共10小题)
11.如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF﹣S△BEF= 2 .
【解答】解:∵点D是AC的中点,
∴AD=AC,
∵S△ABC=12,
∴S△ABD=S△ABC=×12=6.
∵EC=2BE,S△ABC=12,
∴S△ABE=S△ABC=×12=4,
∵S△ABD﹣S△ABE=(S△ADF+S△ABF)﹣(S△ABF+S△BEF)=S△ADF﹣S△BEF,
即S△ADF﹣S△BEF=S△ABD﹣S△ABE=6﹣4=2.
故答案为:2.
12.空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是 三角形具有稳定性 .
【解答】解:这种方法应用的数学知识是:三角形的稳定性,
故答案为:三角形具有稳定性.
13.在一个直角三角形中,已知一个锐角比另一个锐角的4倍多15°,则两个锐角分别为 75°、15° .
【解答】解:设另一个锐角是x,则这个锐角是4x+15°,
根据题意得,x+4x+15°=90°,
解得x=15°,
4x+15°=4×15°+15°=75°,
所以,这两个锐角分别为75°、15°.
故答案为:75°、15°.
14.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于 180° .
【解答】解:由题意得:AB=DB,AC=ED,∠A=∠D=90°,
∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),
∴∠1=∠ACB,
∵∠ACB+∠2=180°,
∴∠1+∠2=180°,
故答案为:180°.
15.如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF= 55° .
【解答】解:如图,∵∠DFC+∠AFD=180°,∠AFD=145°,
∴∠CFD=35°.
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,
,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∴∠EDF+∠BDE=∠EDF+∠CFD=90°,
∴∠EDF=55°.
故答案是:55°.
16.如图,点B在AE上,∠CBE=∠DBE,要使△ABC≌△ABD,还需添加一个条件是 BC=BD (填上适当的一个条件即可)
【解答】解:BC=BD,
理由是:∵∠CBE=∠DBE,∠CBE+∠ABC=180°,∠DBE+∠ABD=180°,
∴∠ABC=∠ABD,
在△ABC和△ABD中
∴△ABC≌△ABD,
故答案为:BC=BD.
17.如图,六根木条钉成一个六边形框架ABCDEF,要使框架稳固且不活动,至少还需要添 3 根木条.
【解答】解:根据三角形的稳定性,得
如图:从图中可以看出,要使框架稳固且不活动,至少还需要添3根木条.
18.在△ABC中,∠A:∠B:∠C=2:3:4,则∠C= 80° .
【解答】解:∵∠A:∠B:∠C=2:3:4,
∴设∠A=2x°,∠B=3x°,∠C=4x°,
由三角形内角和定理可得:2x+3x+4x=180,
解得x=20,
∴∠C=4x°=80°,
故答案为:80°.
19.已知三角形三边分别为1,x,5,则整数x= 5 .
【解答】解:根据三角形的三边关系定理可得:5﹣1<x<5+1,
解得:4<x<6,
∵x为整数,
∴x=5,
故答案为:5.
20.若△ABC中,∠ACB是钝角,AD是BC边上的高,若AD=2,BD=3,CD=1,则△ABC的面积等于 2 .
【解答】解:如图.
∵BD=3,CD=1,
∴BC=BD﹣CD=2,
又∵AD是BC边上的高,AD=2,
∴△ABC的面积=BC AD=×2×2=2.
故答案为2.
三、解答题(共10小题)
21.如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.
(1)求∠ADB的度数;
(2)判断△ABE的形状并加以证明;
(3)连接DE,若DE⊥BD,DE=8,求AD的长.
【解答】(1)解:∵BD=BC,∠DBC=60°,
∴△DBC是等边三角形,
∴DB=DC,∠BDC=∠DBC=∠DCB=60°,
在△ADB和△ADC中,
,
∴△ADB≌△ADC(AAS),
∴∠ADB=∠ADC,
∴∠ADB=(360°﹣60°)=150°.
(2)解:结论:△ABE是等边三角形.
理由:∵∠ABE=∠DBC=60°,
∴∠ABD=∠CBE,
在△ABD和△EBC中,
,
∴△ABD≌△EBC,
∴AB=BE,∵∠ABE=60°,
∴△ABE是等边三角形.
(3)解:连接DE.
∵∠BCE=150°,∠DCB=60°,
∴∠DCE=90°,
∵∠EDB=90°,∠BDC=60°,
∴∠EDC=30°,
∴EC=DE=4,
∵△ABD≌△EBC,
∴AD=EC=4.
22.已知:如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.
【解答】解:∵∠BAC=120°,
∴∠2+∠3=60°①
∵∠1=∠2,
∴∠4=∠3=∠1+∠2=2∠2②
把②代入①得:3∠2=60°,
∠2=20°.
∴∠DAC=120°﹣20°=100°.
23.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,AB=DE,BF=CE,AB∥DE,求证:△ABC≌△DEF.
【解答】证明:∵BF=CE,
∴BF+FC=CE+FC,即BC=EF.
∵AB∥DE,
∴∠B=∠E.
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
24.如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离.为什么?
【解答】解:量出DE的长就等于AB的长,理由如下:
在△ABC和△DEC中,,
∴△ABC≌△DEC(SAS),
∴AB=DE.
25.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=42°,∠DAE=18°,求∠C的度数.
【解答】解:∵AD是BC边上的高,∠B=42°,
∴∠BAD=48°,
∵∠DAE=18°,
∴∠BAE=∠BAD﹣∠DAE=30°,
∵AE是∠BAC的平分线,
∴∠BAC=2∠BAE=60°,
∴∠C=180°﹣∠B﹣∠BAC=78°.
26.如图,点C是线段AB外一点,用没有刻度直尺和圆规画图:
(1)画射线CB;
(2)画直线AC;
(3)①延长线段AB到E,使AE=3AB;
②在①的条件下,如果AB=2cm,那么BE= 4 cm.
【解答】解:(1)如图所示,射线CB即为所求;
(2)如图所示,直线AC即为所求;
(3)①如图所示,线段AE即为所求;
②∵AB=2cm,AE=3AB,
∴AE=6cm.
则BE=AE﹣AB=4cm.
故答案为:4.
27.如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC中边BC上的高AD;
(2)画出△ABC中边AC上的中线BE;
(3)直接写出△ABE的面积为 4 .
【解答】解:(1)如图所示,线段AD即为所求;
(2)如图所示,线段BE即为所求;
(3)S△ABC=BC AD=4×4=8.
∴△ABE的面积=S△ABC=4,
故答案为:4.
28.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BED=55°,求∠BAD的度数;
(2)作△BED的边BD边上的高;
(3)若△ABC的面积为20,BD=2.5,求△BDE中BD边上的高.
【解答】解:(1)∵∠BED=∠ABE+∠BAD,∠ABE=15°,∠BED=55°,
∴∠BAD=∠BED﹣∠ABE=55°﹣15°=40°.
(2)如图,作EF⊥BC于F,则EF为BD边上的高;
(3)∵AD为△ABC的中线,
∴S△ABD=S△ACD=S△ABC,
∵BE为△ABD的中线,
∴S△ABE=S△BED=S△ABD,
∵S△ABC=20,
∴S△BED=BD EF=5,
∵BD=2.5,
∴EF=4
∴△BDE中BD边上的高为4.
29.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
【解答】解:在Rt△ABF中,∠A=70°,CE,BF是两条高,
∴∠EBF=20°,∠ECA=20°,
又∵∠BCE=30°,
∴∠ACB=50°,
∴在Rt△BCF中∠FBC=40°.
30.已知a、b、c为三角形三边的长,化简:|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|.
【解答】解:∵a、b、c为三角形三边的长,
∴a+b>c,a+c>b,b+c>a,
∴原式=|a﹣(b+c)|+|b﹣(c+a)|+|c﹣(a+b)|
=b+c﹣a+a+c﹣b+a+b﹣c
=a+b+c.
第1页(共1页)
一、选择题(共10小题)
1.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
2.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
3.如图,BP是△ABC中∠ABC的平分线,CP是△ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )
A.70° B.80° C.90° D.100°
4.如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
A.三边高的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三边中线的交点
5.如图,小明书上的三角形被墨迹遮挡了一部分,但他很快想到办法在作业本上画了一样的三角形,那么这两个三角形完全一样的依据是( )
A.AAS B.ASA C.SSS D.SAS
6.已知锐角三角形的边长是2,3,x,那么第三边x的取值范围是( )
A.1<x< B. C. D.
7.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
8.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是( )
A.m+n>b+c B.m+n<b+c C.m+n=b+c D.无法确定
9.如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为( )
A.27° B.59° C.69° D.79°
10.下列四种基本尺规作图分别表示,则对应选项中作法错误的是( )
A.作一个角等于已知角
B.作一个角的平分线
C.作一条线段的垂直平分线
D.过直线外一点P作已知直线的垂线
二、填空题(共10小题)
11.如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF﹣S△BEF= .
12.空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是 .
13.在一个直角三角形中,已知一个锐角比另一个锐角的4倍多15°,则两个锐角分别为 .
14.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于 .
15.如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF= .
16.如图,点B在AE上,∠CBE=∠DBE,要使△ABC≌△ABD,还需添加一个条件是 (填上适当的一个条件即可)
17.如图,六根木条钉成一个六边形框架ABCDEF,要使框架稳固且不活动,至少还需要添 根木条.
18.在△ABC中,∠A:∠B:∠C=2:3:4,则∠C= .
19.已知三角形三边分别为1,x,5,则整数x= .
20.若△ABC中,∠ACB是钝角,AD是BC边上的高,若AD=2,BD=3,CD=1,则△ABC的面积等于 .
三、解答题(共10小题)
21.如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.
(1)求∠ADB的度数;
(2)判断△ABE的形状并加以证明;
(3)连接DE,若DE⊥BD,DE=8,求AD的长.
22.已知:如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.
23.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,AB=DE,BF=CE,AB∥DE,求证:△ABC≌△DEF.
24.如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离.为什么?
25.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=42°,∠DAE=18°,求∠C的度数.
26.如图,点C是线段AB外一点,用没有刻度直尺和圆规画图:
(1)画射线CB;
(2)画直线AC;
(3)①延长线段AB到E,使AE=3AB;
②在①的条件下,如果AB=2cm,那么BE= cm.
27.如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC中边BC上的高AD;
(2)画出△ABC中边AC上的中线BE;
(3)直接写出△ABE的面积为 .
28.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BED=55°,求∠BAD的度数;
(2)作△BED的边BD边上的高;
(3)若△ABC的面积为20,BD=2.5,求△BDE中BD边上的高.
29.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
30.已知a、b、c为三角形三边的长,化简:|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|.
北师大新版七年级(下)《第4章 三角形》单元测试卷(2)
参考答案与试题解析
一、选择题(共10小题)
1.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
【解答】解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
2.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
【解答】解:∵AB=AC,∠BAE=∠CAD,
∴当添加AE=AD时,可根据“SAS”判断△ABE≌△ACD;
当添加∠B=∠C时,可根据“ASA”判断△ABE≌△ACD;
当添加∠AEB=∠ADC时,可根据“AAS”判断△ABE≌△ACD.
故选:C.
3.如图,BP是△ABC中∠ABC的平分线,CP是△ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )
A.70° B.80° C.90° D.100°
【解答】解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∵∠ABP=20°,∠ACP=50°,
∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,
∴∠A=∠ACM﹣∠ABC=60°,
∠ACB=180°﹣∠ACM=80°,
∴∠BCP=∠ACB+∠ACP=130°,
∵∠PBC=20°,
∴∠P=180°﹣∠PBC﹣∠BCP=30°,
∴∠A+∠P=90°,
故选:C.
4.如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
A.三边高的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三边中线的交点
【解答】解:∵支撑点应是三角形的重心,
∴三角形的重心是三角形三边中线的交点,
故选:D.
5.如图,小明书上的三角形被墨迹遮挡了一部分,但他很快想到办法在作业本上画了一样的三角形,那么这两个三角形完全一样的依据是( )
A.AAS B.ASA C.SSS D.SAS
【解答】解:由图可知,三角形两角及夹边可以作出,
所以,依据是ASA.
故选:B.
6.已知锐角三角形的边长是2,3,x,那么第三边x的取值范围是( )
A.1<x< B. C. D.
【解答】解:首先要能组成三角形,易得 1<x<5
下面求该三角形为直角三角形的边长情况(此为临界情况),显然长度为2的边对应的角必为锐角(2<3,短边对小角)则只要考虑3或者x为斜边的情况.
3为斜边时,由勾股定理,22+x2=32,得x=√5 作出图形,固定2边,旋转3边易知当1<x<√5 时,该三角形是以3为最大边的钝角三角形;
x 为斜边时,由勾股定理,22+32=x2,得x=√13,同样作图可得 当√13<x<5时,该三角形是以x为最大边的钝角三角形.
综上可知,当√5<x<√13 时,原三角形为锐角三角形.
故选:B.
7.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
【解答】解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,直角三角形沿虚线剪开即可得到一个直角三角形和一个钝角三角形.
因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.
综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.
故选:C.
8.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是( )
A.m+n>b+c B.m+n<b+c C.m+n=b+c D.无法确定
【解答】解:在BA的延长线上取点E,使AE=AC,连接EP,
∵AD是∠BAC的外角平分线,
∴∠CAD=∠EAD,
在△ACP和△AEP中,,
∴△ACP≌△AEP(SAS),
∴PE=PC,
在△PBE中,PB+PE>AB+AE,
∵PB=m,PC=n,AB=c,AC=b,
∴m+n>b+c.
故选:A.
9.如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,此时∠C′DB=74°,则原三角形的∠C的度数为( )
A.27° B.59° C.69° D.79°
【解答】解如图,∵△ABC沿BE将此三角形对折,又沿BA′再一次对折,点C落在BE上的C′处,
∴∠1=∠2,∠2=∠3,∠CDB=∠C′DB=74°,
∴∠1=∠2=∠3,
∴∠ABC=3∠3,
在△BCD中,∠3+∠C+∠CDB=180°,
∴∠3+∠C=180°﹣74°=106°,
在△ABC中,
∵∠A+∠ABC+∠C=180°,
∴20°+2∠3+(∠3+∠C)=180°,
即20°+2∠3+106°=180°,
∴∠3=27°,
∴∠C=106°﹣27°=79°,
故选:D.
10.下列四种基本尺规作图分别表示,则对应选项中作法错误的是( )
A.作一个角等于已知角
B.作一个角的平分线
C.作一条线段的垂直平分线
D.过直线外一点P作已知直线的垂线
【解答】解:①作一个角等于已知角的方法正确;
②作一个角的平分线的作法正确;
③作一条线段的垂直平分线缺少另一个交点,作法错误;
④过直线外一点P作已知直线的垂线的作法正确.
故选:C.
二、填空题(共10小题)
11.如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF﹣S△BEF= 2 .
【解答】解:∵点D是AC的中点,
∴AD=AC,
∵S△ABC=12,
∴S△ABD=S△ABC=×12=6.
∵EC=2BE,S△ABC=12,
∴S△ABE=S△ABC=×12=4,
∵S△ABD﹣S△ABE=(S△ADF+S△ABF)﹣(S△ABF+S△BEF)=S△ADF﹣S△BEF,
即S△ADF﹣S△BEF=S△ABD﹣S△ABE=6﹣4=2.
故答案为:2.
12.空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是 三角形具有稳定性 .
【解答】解:这种方法应用的数学知识是:三角形的稳定性,
故答案为:三角形具有稳定性.
13.在一个直角三角形中,已知一个锐角比另一个锐角的4倍多15°,则两个锐角分别为 75°、15° .
【解答】解:设另一个锐角是x,则这个锐角是4x+15°,
根据题意得,x+4x+15°=90°,
解得x=15°,
4x+15°=4×15°+15°=75°,
所以,这两个锐角分别为75°、15°.
故答案为:75°、15°.
14.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于 180° .
【解答】解:由题意得:AB=DB,AC=ED,∠A=∠D=90°,
∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),
∴∠1=∠ACB,
∵∠ACB+∠2=180°,
∴∠1+∠2=180°,
故答案为:180°.
15.如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF= 55° .
【解答】解:如图,∵∠DFC+∠AFD=180°,∠AFD=145°,
∴∠CFD=35°.
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,
,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∴∠EDF+∠BDE=∠EDF+∠CFD=90°,
∴∠EDF=55°.
故答案是:55°.
16.如图,点B在AE上,∠CBE=∠DBE,要使△ABC≌△ABD,还需添加一个条件是 BC=BD (填上适当的一个条件即可)
【解答】解:BC=BD,
理由是:∵∠CBE=∠DBE,∠CBE+∠ABC=180°,∠DBE+∠ABD=180°,
∴∠ABC=∠ABD,
在△ABC和△ABD中
∴△ABC≌△ABD,
故答案为:BC=BD.
17.如图,六根木条钉成一个六边形框架ABCDEF,要使框架稳固且不活动,至少还需要添 3 根木条.
【解答】解:根据三角形的稳定性,得
如图:从图中可以看出,要使框架稳固且不活动,至少还需要添3根木条.
18.在△ABC中,∠A:∠B:∠C=2:3:4,则∠C= 80° .
【解答】解:∵∠A:∠B:∠C=2:3:4,
∴设∠A=2x°,∠B=3x°,∠C=4x°,
由三角形内角和定理可得:2x+3x+4x=180,
解得x=20,
∴∠C=4x°=80°,
故答案为:80°.
19.已知三角形三边分别为1,x,5,则整数x= 5 .
【解答】解:根据三角形的三边关系定理可得:5﹣1<x<5+1,
解得:4<x<6,
∵x为整数,
∴x=5,
故答案为:5.
20.若△ABC中,∠ACB是钝角,AD是BC边上的高,若AD=2,BD=3,CD=1,则△ABC的面积等于 2 .
【解答】解:如图.
∵BD=3,CD=1,
∴BC=BD﹣CD=2,
又∵AD是BC边上的高,AD=2,
∴△ABC的面积=BC AD=×2×2=2.
故答案为2.
三、解答题(共10小题)
21.如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.
(1)求∠ADB的度数;
(2)判断△ABE的形状并加以证明;
(3)连接DE,若DE⊥BD,DE=8,求AD的长.
【解答】(1)解:∵BD=BC,∠DBC=60°,
∴△DBC是等边三角形,
∴DB=DC,∠BDC=∠DBC=∠DCB=60°,
在△ADB和△ADC中,
,
∴△ADB≌△ADC(AAS),
∴∠ADB=∠ADC,
∴∠ADB=(360°﹣60°)=150°.
(2)解:结论:△ABE是等边三角形.
理由:∵∠ABE=∠DBC=60°,
∴∠ABD=∠CBE,
在△ABD和△EBC中,
,
∴△ABD≌△EBC,
∴AB=BE,∵∠ABE=60°,
∴△ABE是等边三角形.
(3)解:连接DE.
∵∠BCE=150°,∠DCB=60°,
∴∠DCE=90°,
∵∠EDB=90°,∠BDC=60°,
∴∠EDC=30°,
∴EC=DE=4,
∵△ABD≌△EBC,
∴AD=EC=4.
22.已知:如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.
【解答】解:∵∠BAC=120°,
∴∠2+∠3=60°①
∵∠1=∠2,
∴∠4=∠3=∠1+∠2=2∠2②
把②代入①得:3∠2=60°,
∠2=20°.
∴∠DAC=120°﹣20°=100°.
23.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,AB=DE,BF=CE,AB∥DE,求证:△ABC≌△DEF.
【解答】证明:∵BF=CE,
∴BF+FC=CE+FC,即BC=EF.
∵AB∥DE,
∴∠B=∠E.
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
24.如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离.为什么?
【解答】解:量出DE的长就等于AB的长,理由如下:
在△ABC和△DEC中,,
∴△ABC≌△DEC(SAS),
∴AB=DE.
25.如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=42°,∠DAE=18°,求∠C的度数.
【解答】解:∵AD是BC边上的高,∠B=42°,
∴∠BAD=48°,
∵∠DAE=18°,
∴∠BAE=∠BAD﹣∠DAE=30°,
∵AE是∠BAC的平分线,
∴∠BAC=2∠BAE=60°,
∴∠C=180°﹣∠B﹣∠BAC=78°.
26.如图,点C是线段AB外一点,用没有刻度直尺和圆规画图:
(1)画射线CB;
(2)画直线AC;
(3)①延长线段AB到E,使AE=3AB;
②在①的条件下,如果AB=2cm,那么BE= 4 cm.
【解答】解:(1)如图所示,射线CB即为所求;
(2)如图所示,直线AC即为所求;
(3)①如图所示,线段AE即为所求;
②∵AB=2cm,AE=3AB,
∴AE=6cm.
则BE=AE﹣AB=4cm.
故答案为:4.
27.如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC中边BC上的高AD;
(2)画出△ABC中边AC上的中线BE;
(3)直接写出△ABE的面积为 4 .
【解答】解:(1)如图所示,线段AD即为所求;
(2)如图所示,线段BE即为所求;
(3)S△ABC=BC AD=4×4=8.
∴△ABE的面积=S△ABC=4,
故答案为:4.
28.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BED=55°,求∠BAD的度数;
(2)作△BED的边BD边上的高;
(3)若△ABC的面积为20,BD=2.5,求△BDE中BD边上的高.
【解答】解:(1)∵∠BED=∠ABE+∠BAD,∠ABE=15°,∠BED=55°,
∴∠BAD=∠BED﹣∠ABE=55°﹣15°=40°.
(2)如图,作EF⊥BC于F,则EF为BD边上的高;
(3)∵AD为△ABC的中线,
∴S△ABD=S△ACD=S△ABC,
∵BE为△ABD的中线,
∴S△ABE=S△BED=S△ABD,
∵S△ABC=20,
∴S△BED=BD EF=5,
∵BD=2.5,
∴EF=4
∴△BDE中BD边上的高为4.
29.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
【解答】解:在Rt△ABF中,∠A=70°,CE,BF是两条高,
∴∠EBF=20°,∠ECA=20°,
又∵∠BCE=30°,
∴∠ACB=50°,
∴在Rt△BCF中∠FBC=40°.
30.已知a、b、c为三角形三边的长,化简:|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|.
【解答】解:∵a、b、c为三角形三边的长,
∴a+b>c,a+c>b,b+c>a,
∴原式=|a﹣(b+c)|+|b﹣(c+a)|+|c﹣(a+b)|
=b+c﹣a+a+c﹣b+a+b﹣c
=a+b+c.
第1页(共1页)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
