湖南省浏阳市第六中学2011-2012学年高二下学期期末考试数学(理)试题
文档属性
| 名称 | 湖南省浏阳市第六中学2011-2012学年高二下学期期末考试数学(理)试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 441.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-21 00:00:00 | ||
图片预览


文档简介
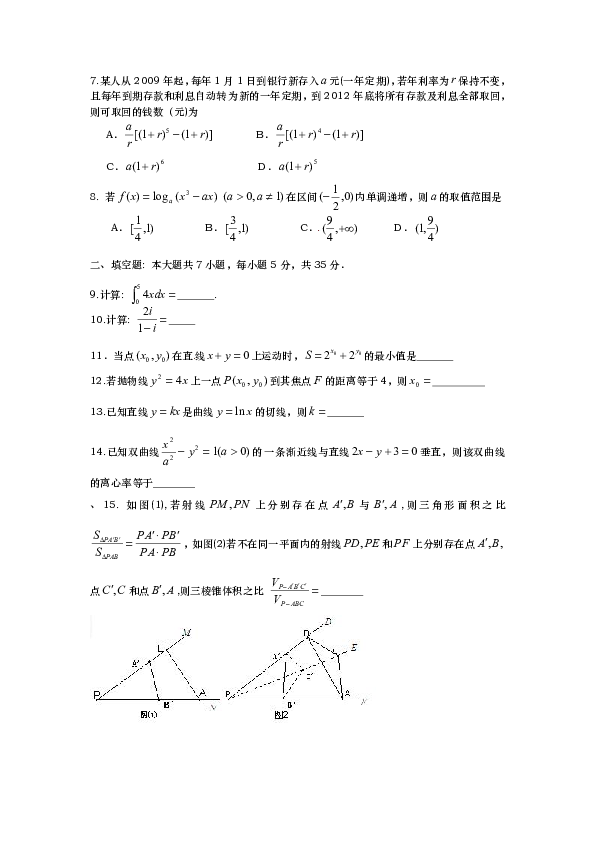
一、选择题:本大题共8小题,每小题5分,共40分.
1.不等式的解集是
A. B. C. D.
2.等差数列:1,4,7,……中,当时,序号等于
A.99 B.100 C.96 D.101
3.“” 是“”的
A.充分条件但不是必要条件 B.必要条件但不是充分条件
C.充要条件 D.既不充分也不必要
4. 在同一坐标系中,方程与 (>> 0 )的曲线大致是
5.全称命题:的否定是
A. B.
C. D.
6.函数在定义域内可导,其图像如图所示.记的导函数为
,则不等式的解集为
A. B.
C. D.
7.某人从2009年起,每年1月1日到银行新存入元(一年定期),若年利率为保持不变,且每年到期存款和利息自动转为新的一年定期,到2012年底将所有存款及利息全部取回,则可取回的钱数(元)为
A. B.
C. D.
8. 若在区间内单调递增,则的取值范围是
A. B. C. D.
二、填空题: 本大题共7小题,每小题5分,共35分.
9.计算: .
10.计算:
11.当点在直线上运动时,的最小值是
12.若抛物线上一点到其焦点的距离等于4,则
13.已知直线是曲线的切线,则
14.已知双曲线的一条渐近线与直线垂直,则该双曲线的离心率等于
、15. 如图(1),若射线上分别存在点与,则三角形面积之比 ,如图(2)若不在同一平面内的射线和上分别存在点点和点,则三棱锥体积之比
三、解答题: 本大题共6小题,满分75分.
16. (本题满分12分)
设是公差的等差数列,是各项都为正数的等比数列,且,
.
(1)求数列和的通项公式;
(2)设…),求数列的前项和.
17. (本题满分12分)
某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台,且冰箱至少生产20台.已知生产这些家电产品每台所需工时和每台产值如下表:
家电名称
空调器
彩电
冰箱
工时
产值/千元
4
3
2
问每周生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)
18. (本题满分12分)
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量(升)关于行驶速度(千米/小时)的函数解析式可以表示为:已知甲、乙两地相距100千米。
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
19. (本题满分13分)
已知四棱锥的底面为直角梯形,,底面,且,是的中点.
(1)求与所成的角余弦值;
(2)在线段上是否存在点,使得平面,若存在.指出点所在位置;若不存在,请说明理由.
20. (本题满分13分)
已知椭圆的长轴长是短轴长的2倍, 分别是它的左、右焦点,点是椭圆上一点, 的周长等于.
(1)求椭圆的方程;
(2)过定点作直线与椭圆交于不同的两点,且(其中为坐标原点),求直线的方程.
21. (本题满分13分)
设函数,且,其中是自然对数的底数.
(1)求与的关系;
(2)若在其定义域内为单调函数,求的取值范围;
(3)设,若在上至少存在一点,使得>成立,求实数的取值范围.
同课章节目录
