10.3频率与概率 同步练习(Word版含解析)
文档属性
| 名称 | 10.3频率与概率 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 333.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 00:00:00 | ||
图片预览




文档简介
人教A版(2019)必修第二册 10.3 频率与概率 同步练习
一、单选题
1.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是
A. B. C. D.
2.近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收垃圾和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾的分类投放情况,现随机抽取了该市三类垃圾箱中总计生活垃圾,经分拣以后统计数据如下表(单位:t).根据样本估计本市生活垃圾的分类投放情况,则下列说法正确的是( )
“厨余垃圾”箱 “可回收垃圾”箱 “其他垃圾”箱
厨余垃圾 400 100 100
可回收垃圾 30 240 30
其他垃圾 20 20 60
A.厨余垃圾投放错误的概率为
B.居民生活垃圾投放正确的概率为
C.该市三类垃圾中投放正确的概率最高的是其他垃圾
D.厨余垃圾在“厨余垃圾”箱、“可回收垃圾”箱、“其他垃圾”箱的投放量的方差为20000
3.下列说法正确的是( )
A.投掷一枚硬币1000次,一定有500次“正面朝上”
B.若甲组数据的方差是,乙组数据的方差是,则甲组数据比乙组数据稳定
C.为了解我国中学生的视力情况,应采取全面调查的方式
D.一组数据1 2 5 5 5 3 3的中位数和众数都是5
4.从数字中随机取两个不同的数,分别记为和,则为整数的概率是( )
A. B. C. D.
5.将一个容量为1000的样本分成若干组,已知某组的频率为0.4,则该组的频数是( )
A.4 B.40 C.250 D.400
6.气象台预报“本市明天降雨概率是70%”,下列说法正确的是( )
A.本市明天将有70%的地区降雨 B.本市有天将有70%的时间降雨
C.明天出行不带雨具淋雨的可能性很大 D.明天出行不带雨具肯定要淋雨
7.一个容量为20的样本数据,分组后组距为10,区间与频数分布如下:(10,20],2;(20,30],3;(30,40],4;(40,50],5;(50,60],4;(60,70],2.则样本在(10,50]上的频率为( )
A. B. C. D.
8.“不怕一万,就怕万一”这句民间谚语说明( ).
A.小概率事件虽很少发生,但也可能发生,需提防;
B.小概率事件很少发生,不用怕;
C.小概率事件就是不可能事件,不会发生;
D.大概率事件就是必然事件,一定发生.
9.若随机事件,互斥,,发生的概率均不等于0,且,,则实数的取值范围是
A. B. C. D.
10.某家庭准备晚上在餐馆吃饭,他们查看了两个网站关于四家餐馆的好评率,如下表所示,考虑每家餐馆的总好评率,他们应选择( )
网站①评价人数 网站①好评率 网站②评价人数 网站②好评率
餐馆甲 1000 95% 1000 85%
餐馆乙 1000 100% 2000 80%
餐馆丙 1000 90% 1000 90%
餐馆丁 2000 95% 1000 85%
A.餐馆甲 B.餐馆乙 C.餐馆丙 D.餐馆丁
11.已知某工厂生产的产品的合格率为90%现采用随机模拟的方法估计4件产品中至少有3件为合格品的概率:先由计算器产生0到9之间取整数值的随机数,指定0表示不是合格品,1,2,3,4,5,6,7,8,9表示是合格品;再以每4个随机数为一组,代表4件产品,经随机模拟产生了如下20组随机数:
7527 0293 7040 9857 0347 4373 8636 6947 1417 4698
0301 6233 2616 8045 6001 3661 9597 7424 7610 4001
掘此估计,4件产品中至少有3件合格品的概率为( )
A. B. C. D.
12.对于总数的一批零件,抽取一个容量为30的样本.若每个零件被抽到的可能性均为25%,则( )
A.120 B.150 C.200 D.240
二、填空题
13.容量为20的样本数据,分组后的频数如下表:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 2 3 4 5 4 2
则样本数据落在区间[10,40)的频率为________.
14.如图所示电路中,开关、、断开的概率分别是0.3、0.2、0.1,且开关、、断开是相互独立的,则此电路连通的概率为________
15.有三台车床加工同一型号的零件,第一台加工的次品率为0.06,第二三台加工的次品率均为0.05,加工出来的零件混放在一起.已知第一,二,三台车床加工的零件数分别占总数的0.25,0.3,0.45,任取一个零件,求它是次品的概率______.
16.在一次数学考试中,某班学生的及格率是,这里所说的“”是指___________.(填“频率”或“概率”)
17.从一堆苹果中任取10只,称得它们的质量(单位:g)如下.
125 120 122 105 130 114 116 95 120 134
则样本数据落在内的频率为______.
三、解答题
18.用抛掷1枚一元硬币和1枚五角硬币来模拟孟德尔的豌豆实验,设2枚硬币的正面对应DD,—元硬币的正面与五角硬币的反面对应Dd,一元硬币的反面与五角硬币的正面对应dD,2枚硬币的反面对应dd.抛掷这2枚硬币100次,记下出现DD,Dd,dD和dd的次数,考察你的结果是否基本符合的比例.
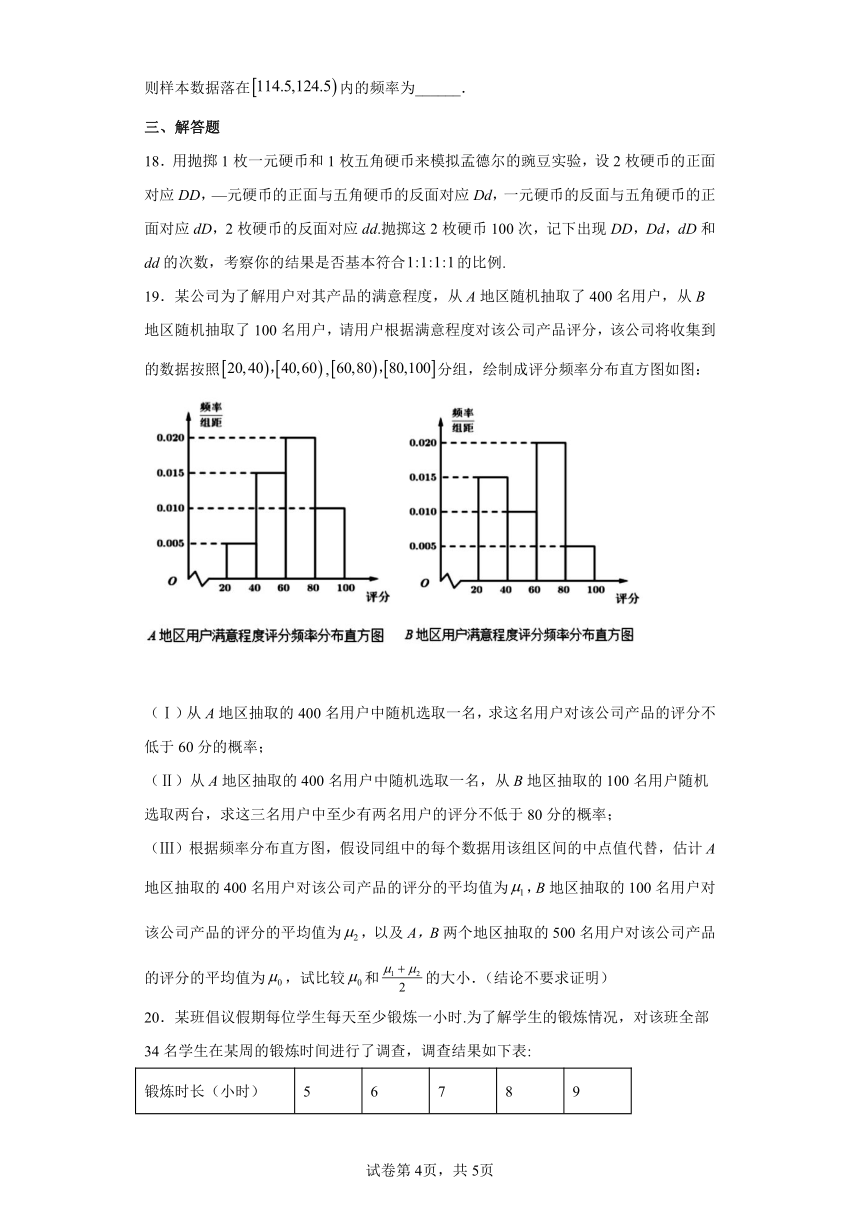
19.某公司为了解用户对其产品的满意程度,从A地区随机抽取了400名用户,从B地区随机抽取了100名用户,请用户根据满意程度对该公司产品评分,该公司将收集到的数据按照,分组,绘制成评分频率分布直方图如图:
(Ⅰ)从A地区抽取的400名用户中随机选取一名,求这名用户对该公司产品的评分不低于60分的概率;
(Ⅱ)从A地区抽取的400名用户中随机选取一名,从B地区抽取的100名用户随机选取两台,求这三名用户中至少有两名用户的评分不低于80分的概率;
(Ⅲ)根据频率分布直方图,假设同组中的每个数据用该组区间的中点值代替,估计A地区抽取的400名用户对该公司产品的评分的平均值为,B地区抽取的100名用户对该公司产品的评分的平均值为,以及A,B两个地区抽取的500名用户对该公司产品的评分的平均值为,试比较和的大小.(结论不要求证明)
20.某班倡议假期每位学生每天至少锻炼一小时.为了解学生的锻炼情况,对该班全部34名学生在某周的锻炼时间进行了调查,调查结果如下表:
锻炼时长(小时) 5 6 7 8 9
男生人数(人) 1 2 4 3 4
女生人数(人) 3 8 6 2 1
(Ⅰ)试根据上述数据,求这个班级女生在该周的平均锻炼时长;
(Ⅱ)若从锻炼8小时的学生中任选2人参加一项活动,求选到男生和女生各1人的概率;
(Ⅲ)试判断该班男生锻炼时长的方差与女生锻炼时长的方差的大小.(直接写出结果)
21.改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】
分析:先确定不超过30的素数,再确定两个不同的数的和等于30的取法,最后根据古典概型概率公式求概率.
详解:不超过30的素数有2,3,5,7,11,13,17,19,23,29,共10个,随机选取两个不同的数,共有种方法,因为,所以随机选取两个不同的数,其和等于30的有3种方法,故概率为,选C.
点睛:古典概型中基本事件数的探求方法: (1)列举法. (2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法. (3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化. (4)排列组合法:适用于限制条件较多且元素数目较多的题目.
2.D
对于A,利用表中的数据可得厨余垃圾投放错误的概率为;对于B,利用表中的数据可得居民生活垃圾投放正确的概率为;对于C,依次求出三类垃圾中投放正确的概率,再比较即可;对于D,利用方差公式求解即可
【详解】
解:对于A,厨余垃圾投放错误的概率为,所以A错误;
对于B,居民生活垃圾投放正确的概率为,所以B错误;
对于C,厨余垃圾投放正确的概率为,可回收垃圾投放正确的概率为,其他垃圾投放正确的概率为,
所以该市三类垃圾中投放正确的概率最高的是可回收垃圾,C错误;
对于D,计算平均数为,
方差为,
所以厨余垃圾在“厨余垃圾”箱、“可回收垃圾”箱、“其他垃圾”箱的投放量的方差为20000,D正确.
故选:D.
3.B
根据统计量,对各项分析判断即可得解.
【详解】
对于A,因为每次抛掷硬币都是随机事件,所以不一定有500次“正面朝上”,故A错误;
对于B,因为方差越小越稳定,故B正确;
对于C,为了解我国中学生的视力情况,应采取抽样调查的方式,故C错误;
对于D,数据1 2 5 5 5 3 3按从小到大排列后为1 2 3 3 5 5 5,
则其中位数为3,故D错误,
故选:B.
4.B
先计算出从数字中随机取两个不同的数,共有种情况,再求出满足为整数的情况,即可求出为整数的概率.
【详解】
解:从数字中随机取两个不同的数,
则有种选法,有种选法,共有种情况;
则满足为整数的情况如下:
当时,或有种情况;
当时,有种情况;
当或时,则不可能为整数,
故共有种情况,
故为整数的概率是:.
故选:B.
5.D
直接利用频率的定义求解即可.
【详解】
一个容量为1000的样本分成若干组,某组的频率为0.4,
该组的频数为:.
故选:.
本题考查频数的求法,解题时要认真审题,属于基础题.
6.C
根据概率的意义,可判断各选项.
【详解】
气象台预报“本市明天降雨概率是70%”,则本市明天降雨的可能性比较大.与降水地区面积和降水时间无关,所以A,B错误.
降水概率是事件发生的可能,不是一定会发生的事情,所以D错误.
而由降水概率是70%,可知降水概率较大,所以明天出行不带雨具淋雨的可能性很大,所以C正确.
故选:C.
本题考查了概率的概念和意义,属于基础题.
7.D
根据频率等于频数比样本容量求解.
【详解】
因为样本在(10,50]上的频数为14,样本容量为20,
所以样本在(10,50]上的频率为
故选:D
本题主要考查统计中频率的求法,属于基础题.
8.A
理解谚语的描述,应用数学概率知识改写即可.
【详解】
“不怕一万,就怕万一” 表示小概率事件很少发生,但也可能发生,需提防;
故选:A
9.D
由随机事件、互斥,、发生的概率均不等于0,知,由此能求出实数的取值范围.
【详解】
随机事件、互斥,、发生的概率均不等于0,
且,,
,即,
解得,即.
故选:D.
本题考查互斥事件的概率的应用,属于基础题.解题时要认真审题,仔细解答.
10.D
根据给定条件求出各餐馆总好评率,再比较大小作答.
【详解】
餐馆甲的总好评率为:,
餐馆乙的总好评率为:,
餐馆丙的好评率为:,
餐馆丁的好评率为:,
显然,所以餐馆丁的总好评率最高.
故选:D
11.D
0表示不是合格品,4件产品中至多出现一次0,根据概率计算公式即可求解.
【详解】
4件产品中至多出现一次0,共个,
所以4件产品中至少有3件合格品的概率为.
故选:D
12.A
根据每个个体被抽到的概率及样本容量,即可求得总体个数.
【详解】
∵对于总数为的一批零件,抽取一个容量为30的样本,每个零件被抽到的可能性均为25%,
∴,
解得.
故选:A.
本题考查了样本容量与抽样概率的关系,属于基础题.
13.0.45
用的频数除以求得的频率.
【详解】
数据落在区间[10,40)的频率为.
故答案为:
本小题主要考查频率的计算,属于基础题.
14.
由题可知当此电路连通时开关联通,至少有一个连通时线路是连通的,再利用分步原理计算即可.
【详解】
由题得当此电路连通时开关联通,至少有一个连通.
故概率为.
故答案为:
本题主要考查了概率的实际运用,需要根据题意分析到连通时满足的情况再求解,属于基础题.
15.
利用三台车床的次品率和零件数占比求得正确结论.
【详解】
依题意,任取一个零件,求它是次品的概率为
.
故答案为:
16.频率
根据频率与概率的概念即可得出答案.
【详解】
解析:在一次数学考试中,某班学生的及格率是,
这里所说的“”是指“频率”.
只有经过很多次考试得到的及格率都是,才能说是概率.
故答案为:频率.
17.0.4
根据频率的计算公式即可求解.
【详解】
解:因为样本数据落在内的有4个:120,122,116,120,
所以样本数据落在内的频率为,
故答案为:0.4.
18.符合
由题意,抛掷1枚一角硬币和1枚五分硬币,出现的可能是正正、正反、反正、反反,每一种情况的概率均为,即可得出结论.
【详解】
由题意,抛掷1枚一角硬币和1枚五分硬币,出现的可能是正正、正反、反正、反反.
每一种情况的概率均为,
抛掷这2枚硬币100次,记下出现,,和的次数,结果基本符合的比例.
19.(Ⅰ)0.6;(Ⅱ)0.036;(Ⅲ)
(Ⅰ)利用频率分布直方图计算评分不低于60分的频率,用频率估计概率即可;
(Ⅱ)先求出A地区随机选取一名,评分不低于80分的概率和B地区随机选取一名,评分不低于80分的概率,再分别求出这三名用户中恰有两名用户的评分不低于80分的概率和
这三名用户的评分都不低于80分的概率,即可求出;
(Ⅲ)利用频率分布直方图分别计算平均值和,再利用加权平均计算,比较即可.
【详解】
(Ⅰ)从A地区抽取的400名用户中随机选取一名,这名用户对该公司产品的评分不低于60分的频率为,
利用频率估计概率可得这名用户对该公司产品的评分不低于60分的概率为0.6;
(Ⅱ)由频率分布图可得A地区随机选取一名,评分不低于80分的概率为,
B地区随机选取一名,评分不低于80分的概率为,
这三名用户中恰有两名用户的评分不低于80分的概率为,
这三名用户的评分都不低于80分的概率为,
则这三名用户中至少有两名用户的评分不低于80分的概率;
(Ⅲ)由A地区用户满意程度评分频率分布直方图可知,
,
由B地区用户满意程度评分频率分布直方图可知,
,
则,
又A地区与B地区抽取用户人数比值为,故A地区抽取用户人数占总数的,B地区抽取用户人数占总数的,
故A,B两个地区抽取的500名用户对该公司产品的评分的平均值,
故.
关键点睛:解决本题的关键是正确利用频率分布直方图对数据进行估计,知道如何用频率估计概率,知道平均数的求解.
20.(Ⅰ)小时(Ⅱ)(Ⅲ)
(Ⅰ)由表中数据计算平均数即可;
(Ⅱ)列举出任选2人的所有情况,再由古典概型的概率公式计算即可;
(Ⅲ)根据数据的离散程度结合方差的性质得出
【详解】
(Ⅰ)这个班级女生在该周的平均锻炼时长为小时
(Ⅱ)由表中数据可知,锻炼8小时的学生中男生有人,记为,女生有人,记为
从中任选2人的所有情况为,,,共种,
其中选到男生和女生各1人的共有种
故选到男生和女生各1人的概率
(Ⅲ)
关键点睛:在第二问中,关键是利用列举法得出所有的情况,再结合古典概型的概率公式进行求解.
21.(Ⅰ)400人;
(Ⅱ);
(Ⅲ)见解析.
(Ⅰ)由题意利用频率近似概率可得满足题意的人数;
(Ⅱ)利用古典概型计算公式可得上个月支付金额大于2000元的概率;
(Ⅲ)结合概率统计相关定义给出结论即可.
【详解】
(Ⅰ)由图表可知仅使用A的人数有30人,仅使用B的人数有25人,
由题意知A,B两种支付方式都不使用的有5人,
所以样本中两种支付方式都使用的有,
所以全校学生中两种支付方式都使用的有(人).
(Ⅱ)因为样本中仅使用B的学生共有25人,只有1人支付金额大于2000元,
所以该学生上个月支付金额大于2000元的概率为.
(Ⅲ)由(Ⅱ)知支付金额大于2000元的概率为,
因为从仅使用B的学生中随机调查1人,发现他本月的支付金额大于2000元,
依据小概率事件它在一次试验中是几乎不可能发生的,所以可以认为仅使用B的学生中本月支付金额大于2000元的人数有变化,且比上个月多.
本题主要考查古典概型概率公式及其应用,概率的定义与应用等知识,意在考查学生的转化能力和计算求解能力.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是
A. B. C. D.
2.近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收垃圾和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾的分类投放情况,现随机抽取了该市三类垃圾箱中总计生活垃圾,经分拣以后统计数据如下表(单位:t).根据样本估计本市生活垃圾的分类投放情况,则下列说法正确的是( )
“厨余垃圾”箱 “可回收垃圾”箱 “其他垃圾”箱
厨余垃圾 400 100 100
可回收垃圾 30 240 30
其他垃圾 20 20 60
A.厨余垃圾投放错误的概率为
B.居民生活垃圾投放正确的概率为
C.该市三类垃圾中投放正确的概率最高的是其他垃圾
D.厨余垃圾在“厨余垃圾”箱、“可回收垃圾”箱、“其他垃圾”箱的投放量的方差为20000
3.下列说法正确的是( )
A.投掷一枚硬币1000次,一定有500次“正面朝上”
B.若甲组数据的方差是,乙组数据的方差是,则甲组数据比乙组数据稳定
C.为了解我国中学生的视力情况,应采取全面调查的方式
D.一组数据1 2 5 5 5 3 3的中位数和众数都是5
4.从数字中随机取两个不同的数,分别记为和,则为整数的概率是( )
A. B. C. D.
5.将一个容量为1000的样本分成若干组,已知某组的频率为0.4,则该组的频数是( )
A.4 B.40 C.250 D.400
6.气象台预报“本市明天降雨概率是70%”,下列说法正确的是( )
A.本市明天将有70%的地区降雨 B.本市有天将有70%的时间降雨
C.明天出行不带雨具淋雨的可能性很大 D.明天出行不带雨具肯定要淋雨
7.一个容量为20的样本数据,分组后组距为10,区间与频数分布如下:(10,20],2;(20,30],3;(30,40],4;(40,50],5;(50,60],4;(60,70],2.则样本在(10,50]上的频率为( )
A. B. C. D.
8.“不怕一万,就怕万一”这句民间谚语说明( ).
A.小概率事件虽很少发生,但也可能发生,需提防;
B.小概率事件很少发生,不用怕;
C.小概率事件就是不可能事件,不会发生;
D.大概率事件就是必然事件,一定发生.
9.若随机事件,互斥,,发生的概率均不等于0,且,,则实数的取值范围是
A. B. C. D.
10.某家庭准备晚上在餐馆吃饭,他们查看了两个网站关于四家餐馆的好评率,如下表所示,考虑每家餐馆的总好评率,他们应选择( )
网站①评价人数 网站①好评率 网站②评价人数 网站②好评率
餐馆甲 1000 95% 1000 85%
餐馆乙 1000 100% 2000 80%
餐馆丙 1000 90% 1000 90%
餐馆丁 2000 95% 1000 85%
A.餐馆甲 B.餐馆乙 C.餐馆丙 D.餐馆丁
11.已知某工厂生产的产品的合格率为90%现采用随机模拟的方法估计4件产品中至少有3件为合格品的概率:先由计算器产生0到9之间取整数值的随机数,指定0表示不是合格品,1,2,3,4,5,6,7,8,9表示是合格品;再以每4个随机数为一组,代表4件产品,经随机模拟产生了如下20组随机数:
7527 0293 7040 9857 0347 4373 8636 6947 1417 4698
0301 6233 2616 8045 6001 3661 9597 7424 7610 4001
掘此估计,4件产品中至少有3件合格品的概率为( )
A. B. C. D.
12.对于总数的一批零件,抽取一个容量为30的样本.若每个零件被抽到的可能性均为25%,则( )
A.120 B.150 C.200 D.240
二、填空题
13.容量为20的样本数据,分组后的频数如下表:
分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
频数 2 3 4 5 4 2
则样本数据落在区间[10,40)的频率为________.
14.如图所示电路中,开关、、断开的概率分别是0.3、0.2、0.1,且开关、、断开是相互独立的,则此电路连通的概率为________
15.有三台车床加工同一型号的零件,第一台加工的次品率为0.06,第二三台加工的次品率均为0.05,加工出来的零件混放在一起.已知第一,二,三台车床加工的零件数分别占总数的0.25,0.3,0.45,任取一个零件,求它是次品的概率______.
16.在一次数学考试中,某班学生的及格率是,这里所说的“”是指___________.(填“频率”或“概率”)
17.从一堆苹果中任取10只,称得它们的质量(单位:g)如下.
125 120 122 105 130 114 116 95 120 134
则样本数据落在内的频率为______.
三、解答题
18.用抛掷1枚一元硬币和1枚五角硬币来模拟孟德尔的豌豆实验,设2枚硬币的正面对应DD,—元硬币的正面与五角硬币的反面对应Dd,一元硬币的反面与五角硬币的正面对应dD,2枚硬币的反面对应dd.抛掷这2枚硬币100次,记下出现DD,Dd,dD和dd的次数,考察你的结果是否基本符合的比例.
19.某公司为了解用户对其产品的满意程度,从A地区随机抽取了400名用户,从B地区随机抽取了100名用户,请用户根据满意程度对该公司产品评分,该公司将收集到的数据按照,分组,绘制成评分频率分布直方图如图:
(Ⅰ)从A地区抽取的400名用户中随机选取一名,求这名用户对该公司产品的评分不低于60分的概率;
(Ⅱ)从A地区抽取的400名用户中随机选取一名,从B地区抽取的100名用户随机选取两台,求这三名用户中至少有两名用户的评分不低于80分的概率;
(Ⅲ)根据频率分布直方图,假设同组中的每个数据用该组区间的中点值代替,估计A地区抽取的400名用户对该公司产品的评分的平均值为,B地区抽取的100名用户对该公司产品的评分的平均值为,以及A,B两个地区抽取的500名用户对该公司产品的评分的平均值为,试比较和的大小.(结论不要求证明)
20.某班倡议假期每位学生每天至少锻炼一小时.为了解学生的锻炼情况,对该班全部34名学生在某周的锻炼时间进行了调查,调查结果如下表:
锻炼时长(小时) 5 6 7 8 9
男生人数(人) 1 2 4 3 4
女生人数(人) 3 8 6 2 1
(Ⅰ)试根据上述数据,求这个班级女生在该周的平均锻炼时长;
(Ⅱ)若从锻炼8小时的学生中任选2人参加一项活动,求选到男生和女生各1人的概率;
(Ⅲ)试判断该班男生锻炼时长的方差与女生锻炼时长的方差的大小.(直接写出结果)
21.改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】
分析:先确定不超过30的素数,再确定两个不同的数的和等于30的取法,最后根据古典概型概率公式求概率.
详解:不超过30的素数有2,3,5,7,11,13,17,19,23,29,共10个,随机选取两个不同的数,共有种方法,因为,所以随机选取两个不同的数,其和等于30的有3种方法,故概率为,选C.
点睛:古典概型中基本事件数的探求方法: (1)列举法. (2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法. (3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化. (4)排列组合法:适用于限制条件较多且元素数目较多的题目.
2.D
对于A,利用表中的数据可得厨余垃圾投放错误的概率为;对于B,利用表中的数据可得居民生活垃圾投放正确的概率为;对于C,依次求出三类垃圾中投放正确的概率,再比较即可;对于D,利用方差公式求解即可
【详解】
解:对于A,厨余垃圾投放错误的概率为,所以A错误;
对于B,居民生活垃圾投放正确的概率为,所以B错误;
对于C,厨余垃圾投放正确的概率为,可回收垃圾投放正确的概率为,其他垃圾投放正确的概率为,
所以该市三类垃圾中投放正确的概率最高的是可回收垃圾,C错误;
对于D,计算平均数为,
方差为,
所以厨余垃圾在“厨余垃圾”箱、“可回收垃圾”箱、“其他垃圾”箱的投放量的方差为20000,D正确.
故选:D.
3.B
根据统计量,对各项分析判断即可得解.
【详解】
对于A,因为每次抛掷硬币都是随机事件,所以不一定有500次“正面朝上”,故A错误;
对于B,因为方差越小越稳定,故B正确;
对于C,为了解我国中学生的视力情况,应采取抽样调查的方式,故C错误;
对于D,数据1 2 5 5 5 3 3按从小到大排列后为1 2 3 3 5 5 5,
则其中位数为3,故D错误,
故选:B.
4.B
先计算出从数字中随机取两个不同的数,共有种情况,再求出满足为整数的情况,即可求出为整数的概率.
【详解】
解:从数字中随机取两个不同的数,
则有种选法,有种选法,共有种情况;
则满足为整数的情况如下:
当时,或有种情况;
当时,有种情况;
当或时,则不可能为整数,
故共有种情况,
故为整数的概率是:.
故选:B.
5.D
直接利用频率的定义求解即可.
【详解】
一个容量为1000的样本分成若干组,某组的频率为0.4,
该组的频数为:.
故选:.
本题考查频数的求法,解题时要认真审题,属于基础题.
6.C
根据概率的意义,可判断各选项.
【详解】
气象台预报“本市明天降雨概率是70%”,则本市明天降雨的可能性比较大.与降水地区面积和降水时间无关,所以A,B错误.
降水概率是事件发生的可能,不是一定会发生的事情,所以D错误.
而由降水概率是70%,可知降水概率较大,所以明天出行不带雨具淋雨的可能性很大,所以C正确.
故选:C.
本题考查了概率的概念和意义,属于基础题.
7.D
根据频率等于频数比样本容量求解.
【详解】
因为样本在(10,50]上的频数为14,样本容量为20,
所以样本在(10,50]上的频率为
故选:D
本题主要考查统计中频率的求法,属于基础题.
8.A
理解谚语的描述,应用数学概率知识改写即可.
【详解】
“不怕一万,就怕万一” 表示小概率事件很少发生,但也可能发生,需提防;
故选:A
9.D
由随机事件、互斥,、发生的概率均不等于0,知,由此能求出实数的取值范围.
【详解】
随机事件、互斥,、发生的概率均不等于0,
且,,
,即,
解得,即.
故选:D.
本题考查互斥事件的概率的应用,属于基础题.解题时要认真审题,仔细解答.
10.D
根据给定条件求出各餐馆总好评率,再比较大小作答.
【详解】
餐馆甲的总好评率为:,
餐馆乙的总好评率为:,
餐馆丙的好评率为:,
餐馆丁的好评率为:,
显然,所以餐馆丁的总好评率最高.
故选:D
11.D
0表示不是合格品,4件产品中至多出现一次0,根据概率计算公式即可求解.
【详解】
4件产品中至多出现一次0,共个,
所以4件产品中至少有3件合格品的概率为.
故选:D
12.A
根据每个个体被抽到的概率及样本容量,即可求得总体个数.
【详解】
∵对于总数为的一批零件,抽取一个容量为30的样本,每个零件被抽到的可能性均为25%,
∴,
解得.
故选:A.
本题考查了样本容量与抽样概率的关系,属于基础题.
13.0.45
用的频数除以求得的频率.
【详解】
数据落在区间[10,40)的频率为.
故答案为:
本小题主要考查频率的计算,属于基础题.
14.
由题可知当此电路连通时开关联通,至少有一个连通时线路是连通的,再利用分步原理计算即可.
【详解】
由题得当此电路连通时开关联通,至少有一个连通.
故概率为.
故答案为:
本题主要考查了概率的实际运用,需要根据题意分析到连通时满足的情况再求解,属于基础题.
15.
利用三台车床的次品率和零件数占比求得正确结论.
【详解】
依题意,任取一个零件,求它是次品的概率为
.
故答案为:
16.频率
根据频率与概率的概念即可得出答案.
【详解】
解析:在一次数学考试中,某班学生的及格率是,
这里所说的“”是指“频率”.
只有经过很多次考试得到的及格率都是,才能说是概率.
故答案为:频率.
17.0.4
根据频率的计算公式即可求解.
【详解】
解:因为样本数据落在内的有4个:120,122,116,120,
所以样本数据落在内的频率为,
故答案为:0.4.
18.符合
由题意,抛掷1枚一角硬币和1枚五分硬币,出现的可能是正正、正反、反正、反反,每一种情况的概率均为,即可得出结论.
【详解】
由题意,抛掷1枚一角硬币和1枚五分硬币,出现的可能是正正、正反、反正、反反.
每一种情况的概率均为,
抛掷这2枚硬币100次,记下出现,,和的次数,结果基本符合的比例.
19.(Ⅰ)0.6;(Ⅱ)0.036;(Ⅲ)
(Ⅰ)利用频率分布直方图计算评分不低于60分的频率,用频率估计概率即可;
(Ⅱ)先求出A地区随机选取一名,评分不低于80分的概率和B地区随机选取一名,评分不低于80分的概率,再分别求出这三名用户中恰有两名用户的评分不低于80分的概率和
这三名用户的评分都不低于80分的概率,即可求出;
(Ⅲ)利用频率分布直方图分别计算平均值和,再利用加权平均计算,比较即可.
【详解】
(Ⅰ)从A地区抽取的400名用户中随机选取一名,这名用户对该公司产品的评分不低于60分的频率为,
利用频率估计概率可得这名用户对该公司产品的评分不低于60分的概率为0.6;
(Ⅱ)由频率分布图可得A地区随机选取一名,评分不低于80分的概率为,
B地区随机选取一名,评分不低于80分的概率为,
这三名用户中恰有两名用户的评分不低于80分的概率为,
这三名用户的评分都不低于80分的概率为,
则这三名用户中至少有两名用户的评分不低于80分的概率;
(Ⅲ)由A地区用户满意程度评分频率分布直方图可知,
,
由B地区用户满意程度评分频率分布直方图可知,
,
则,
又A地区与B地区抽取用户人数比值为,故A地区抽取用户人数占总数的,B地区抽取用户人数占总数的,
故A,B两个地区抽取的500名用户对该公司产品的评分的平均值,
故.
关键点睛:解决本题的关键是正确利用频率分布直方图对数据进行估计,知道如何用频率估计概率,知道平均数的求解.
20.(Ⅰ)小时(Ⅱ)(Ⅲ)
(Ⅰ)由表中数据计算平均数即可;
(Ⅱ)列举出任选2人的所有情况,再由古典概型的概率公式计算即可;
(Ⅲ)根据数据的离散程度结合方差的性质得出
【详解】
(Ⅰ)这个班级女生在该周的平均锻炼时长为小时
(Ⅱ)由表中数据可知,锻炼8小时的学生中男生有人,记为,女生有人,记为
从中任选2人的所有情况为,,,共种,
其中选到男生和女生各1人的共有种
故选到男生和女生各1人的概率
(Ⅲ)
关键点睛:在第二问中,关键是利用列举法得出所有的情况,再结合古典概型的概率公式进行求解.
21.(Ⅰ)400人;
(Ⅱ);
(Ⅲ)见解析.
(Ⅰ)由题意利用频率近似概率可得满足题意的人数;
(Ⅱ)利用古典概型计算公式可得上个月支付金额大于2000元的概率;
(Ⅲ)结合概率统计相关定义给出结论即可.
【详解】
(Ⅰ)由图表可知仅使用A的人数有30人,仅使用B的人数有25人,
由题意知A,B两种支付方式都不使用的有5人,
所以样本中两种支付方式都使用的有,
所以全校学生中两种支付方式都使用的有(人).
(Ⅱ)因为样本中仅使用B的学生共有25人,只有1人支付金额大于2000元,
所以该学生上个月支付金额大于2000元的概率为.
(Ⅲ)由(Ⅱ)知支付金额大于2000元的概率为,
因为从仅使用B的学生中随机调查1人,发现他本月的支付金额大于2000元,
依据小概率事件它在一次试验中是几乎不可能发生的,所以可以认为仅使用B的学生中本月支付金额大于2000元的人数有变化,且比上个月多.
本题主要考查古典概型概率公式及其应用,概率的定义与应用等知识,意在考查学生的转化能力和计算求解能力.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
