第九章 统计 单元练习(Word版含解析)
文档属性
| 名称 | 第九章 统计 单元练习(Word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 540.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 00:00:00 | ||
图片预览




文档简介
人教A版(2019)必修第二册 第九章 统计 同步练习
一、单选题
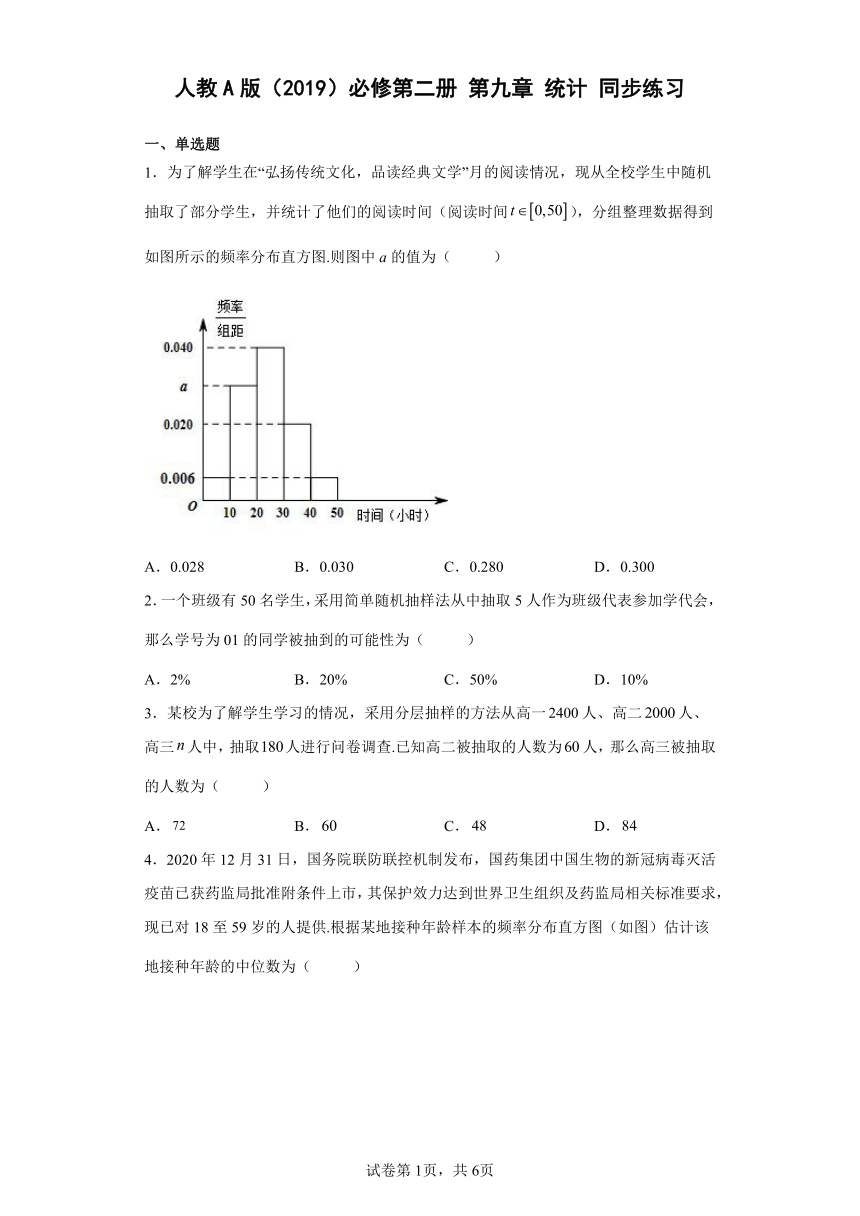
1.为了解学生在“弘扬传统文化,品读经典文学”月的阅读情况,现从全校学生中随机抽取了部分学生,并统计了他们的阅读时间(阅读时间),分组整理数据得到如图所示的频率分布直方图.则图中a的值为( )
A.0.028 B.0.030 C.0.280 D.0.300
2.一个班级有50名学生,采用简单随机抽样法从中抽取5人作为班级代表参加学代会,那么学号为01的同学被抽到的可能性为( )
A.2% B.20% C.50% D.10%
3.某校为了解学生学习的情况,采用分层抽样的方法从高一人、高二人、高三人中,抽取人进行问卷调查.已知高二被抽取的人数为人,那么高三被抽取的人数为( )
A. B. C. D.
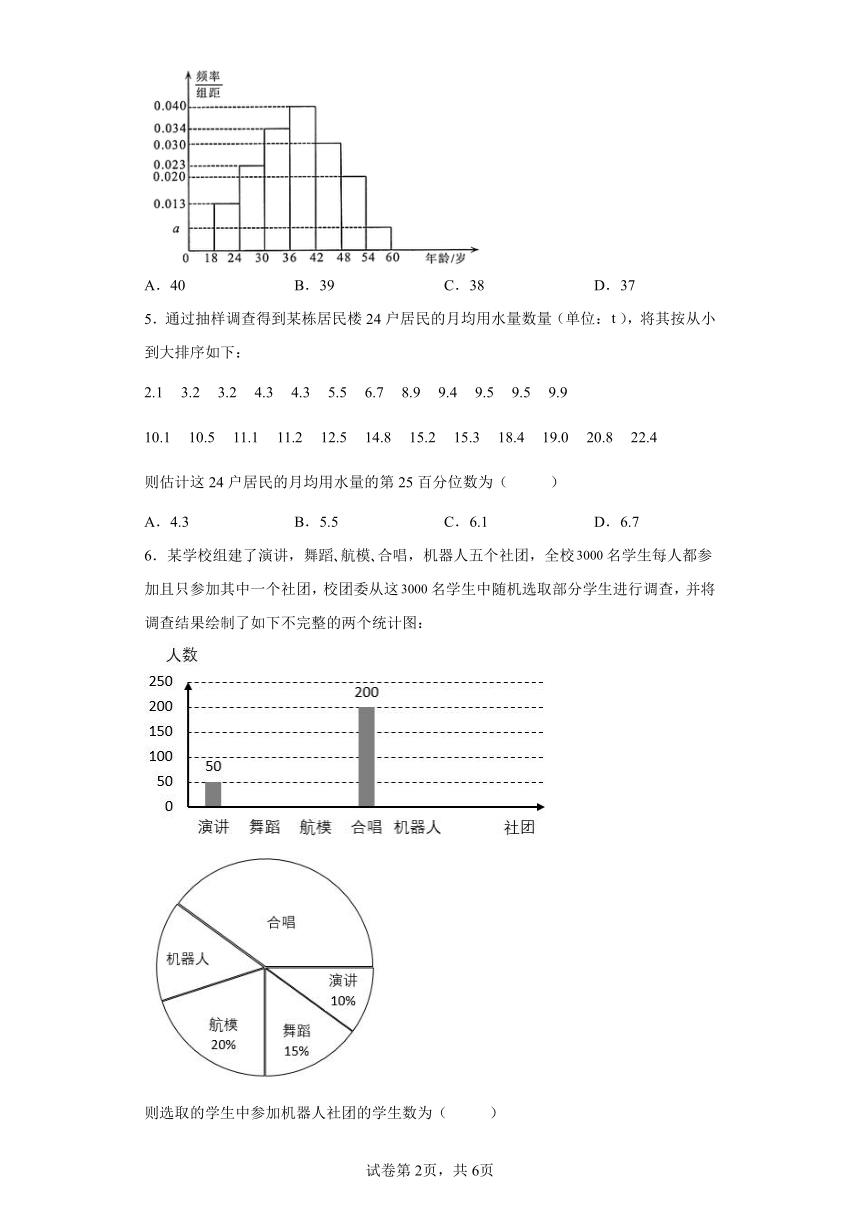
4.2020年12月31日,国务院联防联控机制发布,国药集团中国生物的新冠病毒灭活疫苗已获药监局批准附条件上市,其保护效力达到世界卫生组织及药监局相关标准要求,现已对18至59岁的人提供.根据某地接种年龄样本的频率分布直方图(如图)估计该地接种年龄的中位数为( )
A.40 B.39 C.38 D.37
5.通过抽样调查得到某栋居民楼24户居民的月均用水量数量(单位:),将其按从小到大排序如下:
2.1 3.2 3.2 4.3 4.3 5.5 6.7 8.9 9.4 9.5 9.5 9.9
10.1 10.5 11.1 11.2 12.5 14.8 15.2 15.3 18.4 19.0 20.8 22.4
则估计这24户居民的月均用水量的第25百分位数为( )
A.4.3 B.5.5 C.6.1 D.6.7
6.某学校组建了演讲,舞蹈 航模 合唱,机器人五个社团,全校名学生每人都参加且只参加其中一个社团,校团委从这名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:
则选取的学生中参加机器人社团的学生数为( )
A. B. C. D.
7.某学校高二年级选择“史政地”、“史政生”和“史地生”这三种组合的学生人数分别为210、90和若采用分层抽样的方法从中随机抽取12名学生,则从“史政生”组合中抽取的学生人数为( )
A.7 B.6 C.3 D.2
8.10名工人某天生产同一零件,生产的件数是15、17、14、10、15、17、17、16、14、12.设其平均数为a,中位数为b,众数为c,则有( )
A. B. C. D.
9.若样本数据,,…,的标准差为,则数据,,…,的标准差为( )
A. B. C. D.
10.某班数学课代表统计一次数学测验的平均分与方差,计算完毕才发现忘记把自己的分数录入进去了,只好重算一次.已知原平均分和原方差分别为,s2,新平均分和新方差分别为,,若此同学的得分恰好为,则( )
A., B.,
C., D.,
11.甲,乙,丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图1,图2和图3,若,,分别表示他们测试成绩的标准差,则( )
A. B.
C. D.
12.数据3.2,3.4,3.8,4.2,4.3,4.5,x,6.6的第65百分位数是4.5,则实数x的取值范围是( )
A. B. C. D.
二、填空题
13.若从总体中随机抽取的样本为: 1 1 3 2 2 4 2,则该总体标准差的点估计值是___________.(精确到0.1)
14.某口罩生产工厂为了了解口罩的质量,现利用随机数表对生产的50只口罩进行抽样检测,先将50个零件进行编号为01,02,03,…,50,从中抽取10个样本,下图提供随机数表的第2行到第4行,若从表中第3行第4列开始向右读取数据,则得到的第5个样本编号是__________.
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 15 53 31 34 57 86 01 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
15.《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱,欲以钱数多少衰出之,问各几何?”其意为:“今有甲带了560钱,乙带了350钱,丙带了180钱,三人一起出关,共需要交关税100钱,依照钱的多少按比例出钱”,则丙应出________钱(所得结果四舍五入,保留整数).
16.已知的平均数为,标准差为,且,其中.则的平均数与方差的和为_______.
三、解答题
17.一支田径队有男运动员56人,女运动员42人,按性别进行分层,用分层随机抽样的方法从全体运动员中抽出一个容量为28的样本.如果样本按比例分配,那么男、女运动员应各抽取多少名?
18.某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在的学生人数为6.
(1)求直方图中的值;
(2)求的值;
(3)试根据样本估计“该校高一学生期末数学考试成绩70”的概率.
19.有20种不同的零食,每100g可食部分包含的能量(单位:kJ)如下:
110 120 123 165 432 190 174 235 428 318
249 280 162 146 210 120 123 120 150 140
(1)以上述20个数据组成总体,求总体平均数与总体标准差
(2)设计恰当的随机抽样方法,从总体中抽取一个容量为7的样本.
(3)利用上面的抽样方法,再抽取容量为7的样本,这个样本的平均数和标准差与(2)中的结果一样吗?为什么?
(4)利用(2)中的随机抽样方法,分别从总体中抽取一个容量为10,13,16,19的样本,分析样本容量与样本的平均数和标准差对总体的估计效果之间有什么关系.
20.为了解某市家庭用电量的情况,该市统计局调查了100户居民去年一年的月均用电量,发现他们的用电量都在50kW·h至350kW·h之间,进行适当分组后,画出频率分布直方图如图所示.
(I)求a的值;
(Ⅱ)求被调查用户中,用电量大于250kW·h的户数;
(III)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯定价,希望使80%的居民缴费在第一档(费用最低),请给出第一档用电标准(单位:kW·h)的建议,并简要说明理由.
21.一个经销鲜花产品的微店,为保障售出的百合花品质,每天从云南鲜花基地空运固定数量的百合花,如有剩余则免费分赠给第二天购花顾客,如果不足,则从本地鲜花供应商处进货.今年四月前10天,微店百合花的售价为每支2元,云南空运来的百合花每支进价1.6元,本地供应商处百合花每支进价1.8元,微店这10天的订单中百合花的需求量(单位:支)依次为:251,255,231,243,263,241,265,255,244,252.
(Ⅰ)求今年四月前10天订单中百合花需求量的平均数和众数,并完成频率分布直方图;
(Ⅱ)预计四月的后20天,订单中百合花需求量的频率分布与四月前10天相同,百合花进货价格与售价均不变,请根据(Ⅰ)中频率分布直方图判断(同一组中的需求量数据用该组区间的中点值作代表,位于各区间的频率代替位于该区间的概率),微店每天从云南固定空运250支,还是255支百合花,四月后20天百合花销售总利润会更大?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
根据五个矩形的面积和为1列式可得结果.
【详解】
由得.
故选:A
2.D
根据简单随机抽样的定义,即可求解,
【详解】
每个学生被抽到的可能性都是,
所以学号为01的同学被抽到的可能性为.
故选:D
3.C
利用分层抽样求出的值,进而可求得高三被抽取的人数.
【详解】
由分层抽样可得,可得,
设高三所抽取的人数为,则,解得.
故选:C.
4.C
利用中位数左右两边的小矩形的面积都等于即可求解.
【详解】
年龄位于的频率为,
年龄位于的频率为,
年龄位于的频率为,
年龄位于的频率为,
因为,而
,
所以中位数位于,设中位数为,
则,
解得:,
故选:C.
5.C
利用百分位数的定义求解即可
【详解】
,因为第6个和第7个数据分别为5.5和6.7,
所以估计这24户居民的月均用水量的第25百分位数为.
故选:C
6.B
根据演讲的人数,求得本次调查的人数为人,进而求得机器人所占的比例,即可求解.
【详解】
由题意,本次调查的人数为人,
其中合唱比赛所占的比例为,
所以机器人所占的比例为,
所以选取的学生中参加机器人社团的学生数为人.
故选:B.
7.C
先求出“史政生”所占的比例,然后按比例抽取人数,即可得到答案.
【详解】
由题意可知,“史政地”、“史政生”和“史地生”这三种组合的学生人数分别为210,90和60,
故“史政生”所占的比例为,
由分层抽样是按比例抽取可得,“史政生”组合中抽取的学生人数为.
故选:C
8.B
将样本数据由小到大进行排列,根据定义求出,即可得出结论.
【详解】
解:将生产的件数由小到大排列为:10、12、14、14、15、15、16、17、17、17,
∴ ,中位数为,
众数为,
因此,,
故选:B.
9.B
首先设原数据的平均数为,则新数据的平均数为,然后结合原数据的方差,利用方差的公式计算得出新数据的方差,再求出标准差即可.
【详解】
设原数据的平均数为,则新数据的平均数为,
则原数据的方差为,
则新数据的方差为:
.
故数据,,…,的标准差为:8.
故选:B.
10.C
根据平均数和方差的公式计算即可求解.
【详解】
设这个班有个学生,数据分别为,第个同学没有录入,
第一次计算时总分是,
方差是,
第二次计算时:,
方差
,
所以,,
故选:C.
11.D
先分别求出甲,乙,丙三名运动员射击成绩的平均分,然后根据方差公式求出相应的方差,比较大小可得标准差的大小.
【详解】
甲的平均成绩为,
其方差为
乙的平均成绩为,
其方差为丙的平均成绩为
其方差为.
所以
故选: D
12.A
根据百分位数的定义判断求解.
【详解】
因为,所以这组数据的第65百分位数是第6项数据4.5,
所以应有5个数不大于4.5,则,
故选:A.
13.
利用样本标准差的点估计值估计总体标准差的点估计值即可.
【详解】
解:由已知,样本的平均值为,
所以样本标准差的点估计值为
,
所以总体标准差的点估计值是,
故答案为:.
14..
根据所给数据依次找出前5个数即可.
【详解】
从表中第3行第4列开始向右读取数据,依次为:
所以得到的第5个样本编号是
故答案为:
15.
根据丙所带的钱的比例乘以总关税钱即得所求.
【详解】
依照钱的多少按比例出钱,
所以丙应该出钱为.
故答案为:.
16.
根据平均数、方差的性质计算可得;
【详解】
解:已知,则,
则
故答案为:
17.男生16人,女生12人
先计算得到抽取比例为,再计算得到答案.
【详解】
田径队运动员的总人数是,要得到28人的样本,占总体的比例为,
于是应该在男运动员中随机抽取(人),
在女运动员中随机抽取(人).
本题考查了分层抽样,属于简单题.
18.(1);(2);(3).
(1)由频率分布直方图的高之和为组距分之一,即可得出结果;
(2)根据样本容量、总体与频率之间的关系计算即可得出结果;
(3)用总面积1减去左边2个矩形的面积即可.
【详解】
解:(1)由频率分布直方图的性质得:
,
解得.
(2)∵成绩在的学生人数为6,
由频率分布直方图得成绩在的学生所占频率为:,
∴.
(3)根据样本估计“该校高一学生期末数学考试成绩70”的概率:
.
19.(1)平均数为199.75,总体标准差为95.26;(2)抓阄法;(3)(2)和(3)的计算结果不相同的概率相当大,而相同的概率很小;(4)由于样本的随机性,也有极个别(小概率)的例外情况.
(1)由平均数和方差公式计算;
(2)用抓阄法进行抽样;
(3)由于抽样的随机性,两种结果相同的概率很小,不同概率很大.
(4)由于样本容量增大,估计总体的精确程度会提高,效果更好(也有个别现象效果不好).
【详解】
(1)总体平均数为199.75.
总体标准差为95.26.
(2)可以使用抓阄法进行抽样.
(3)由样本的随机性,知(2)和(3)的计算结果不相同的概率相当大,而相同的概率很小.
(4)随着样本容量的增加,分别用样本平均数和样本标准差估计总体平均数和总体标准差的效果会越来越好(即精度会越来越高).但是由于样本的随机性,也有极个别(小概率)的例外情况.
本题考查用样本估计总体,样本容量越大时,估计效果可能会更好些.
20.(I);(Ⅱ);(III) kW·h.
(1)根据频率和为计算出的值;
(2)根据频率分布直方图计算出“用电量大于250kW·h”的频率,再将该频率乘以对应的总户数即可得到结果;
(3)根据频率分布直方图计算出频率刚好为时对应的月用电量,由此可得到第一档用电标准.
【详解】
(1)因为,所以;
(2)根据频率分布直方图可知:“用电量大于250kW·h”的频率为,
所以用电量大于250kW·h的户数为:,
故用电量大于250kW·h有户;
(3)因为前三组的频率和为:,
前四组的频率之和为,
所以频率为时对应的数据在第四组,
所以第一档用电标准为:kW·h.
故第一档用电标准为 kW·h.
本题考查频率分布直方图的综合应用,主要考查利用频率分布直方图进行相关计算,对学生读取图表信息和计算能力有一定要求,难度一般.
21.(Ⅰ)见解析(Ⅱ)四月后20天总利润更大
(Ⅰ)根据众数的定义直接可求出众为255.利用平均数的公式可以求出平均数.根据给定的分组,通过计算完成频率分布直方图.
(Ⅱ)设订单中百合花需求量为(支),由(Ⅰ)中频率分布直方图,可以求出可能取值、每个可能取值相应频率,每个可能取值相应的天数.分别求出空运250支, 255支百合花时,销售总利润的大小,进行比较,得出结论.
【详解】
解:(Ⅰ)四月前10天订单中百合需求量众数为255,
平均数
频率分布直方图补充如下:
(Ⅱ)设订单中百合花需求量为(支),由(Ⅰ)中频率分布直方图,
可能取值为235,245,255,265,相应频率分别为0.1,0.3,0.4,0.2,
∴20天中相应的天数为2天,6天,8天,4天.
①若空运250支
,当日利润为,
,当日利润为,
,当日利润为,
,当日利润为,
20天总利润为元.
②若空运255支
,当日利润为,
,当日利润为,
,当日利润为,
,当日利润为,
20天总利润为元.
∵,∴每天空运250支百合花四月后20天总利润更大.
本题考查了众数、平均数、频率分布直方图;重点考查了学生通过阅读,提取有用信息,用数学知识解决实际生活问题的能力.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.为了解学生在“弘扬传统文化,品读经典文学”月的阅读情况,现从全校学生中随机抽取了部分学生,并统计了他们的阅读时间(阅读时间),分组整理数据得到如图所示的频率分布直方图.则图中a的值为( )
A.0.028 B.0.030 C.0.280 D.0.300
2.一个班级有50名学生,采用简单随机抽样法从中抽取5人作为班级代表参加学代会,那么学号为01的同学被抽到的可能性为( )
A.2% B.20% C.50% D.10%
3.某校为了解学生学习的情况,采用分层抽样的方法从高一人、高二人、高三人中,抽取人进行问卷调查.已知高二被抽取的人数为人,那么高三被抽取的人数为( )
A. B. C. D.
4.2020年12月31日,国务院联防联控机制发布,国药集团中国生物的新冠病毒灭活疫苗已获药监局批准附条件上市,其保护效力达到世界卫生组织及药监局相关标准要求,现已对18至59岁的人提供.根据某地接种年龄样本的频率分布直方图(如图)估计该地接种年龄的中位数为( )
A.40 B.39 C.38 D.37
5.通过抽样调查得到某栋居民楼24户居民的月均用水量数量(单位:),将其按从小到大排序如下:
2.1 3.2 3.2 4.3 4.3 5.5 6.7 8.9 9.4 9.5 9.5 9.9
10.1 10.5 11.1 11.2 12.5 14.8 15.2 15.3 18.4 19.0 20.8 22.4
则估计这24户居民的月均用水量的第25百分位数为( )
A.4.3 B.5.5 C.6.1 D.6.7
6.某学校组建了演讲,舞蹈 航模 合唱,机器人五个社团,全校名学生每人都参加且只参加其中一个社团,校团委从这名学生中随机选取部分学生进行调查,并将调查结果绘制了如下不完整的两个统计图:
则选取的学生中参加机器人社团的学生数为( )
A. B. C. D.
7.某学校高二年级选择“史政地”、“史政生”和“史地生”这三种组合的学生人数分别为210、90和若采用分层抽样的方法从中随机抽取12名学生,则从“史政生”组合中抽取的学生人数为( )
A.7 B.6 C.3 D.2
8.10名工人某天生产同一零件,生产的件数是15、17、14、10、15、17、17、16、14、12.设其平均数为a,中位数为b,众数为c,则有( )
A. B. C. D.
9.若样本数据,,…,的标准差为,则数据,,…,的标准差为( )
A. B. C. D.
10.某班数学课代表统计一次数学测验的平均分与方差,计算完毕才发现忘记把自己的分数录入进去了,只好重算一次.已知原平均分和原方差分别为,s2,新平均分和新方差分别为,,若此同学的得分恰好为,则( )
A., B.,
C., D.,
11.甲,乙,丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图1,图2和图3,若,,分别表示他们测试成绩的标准差,则( )
A. B.
C. D.
12.数据3.2,3.4,3.8,4.2,4.3,4.5,x,6.6的第65百分位数是4.5,则实数x的取值范围是( )
A. B. C. D.
二、填空题
13.若从总体中随机抽取的样本为: 1 1 3 2 2 4 2,则该总体标准差的点估计值是___________.(精确到0.1)
14.某口罩生产工厂为了了解口罩的质量,现利用随机数表对生产的50只口罩进行抽样检测,先将50个零件进行编号为01,02,03,…,50,从中抽取10个样本,下图提供随机数表的第2行到第4行,若从表中第3行第4列开始向右读取数据,则得到的第5个样本编号是__________.
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 15 53 31 34 57 86 01 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
15.《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱,欲以钱数多少衰出之,问各几何?”其意为:“今有甲带了560钱,乙带了350钱,丙带了180钱,三人一起出关,共需要交关税100钱,依照钱的多少按比例出钱”,则丙应出________钱(所得结果四舍五入,保留整数).
16.已知的平均数为,标准差为,且,其中.则的平均数与方差的和为_______.
三、解答题
17.一支田径队有男运动员56人,女运动员42人,按性别进行分层,用分层随机抽样的方法从全体运动员中抽出一个容量为28的样本.如果样本按比例分配,那么男、女运动员应各抽取多少名?
18.某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在的学生人数为6.
(1)求直方图中的值;
(2)求的值;
(3)试根据样本估计“该校高一学生期末数学考试成绩70”的概率.
19.有20种不同的零食,每100g可食部分包含的能量(单位:kJ)如下:
110 120 123 165 432 190 174 235 428 318
249 280 162 146 210 120 123 120 150 140
(1)以上述20个数据组成总体,求总体平均数与总体标准差
(2)设计恰当的随机抽样方法,从总体中抽取一个容量为7的样本.
(3)利用上面的抽样方法,再抽取容量为7的样本,这个样本的平均数和标准差与(2)中的结果一样吗?为什么?
(4)利用(2)中的随机抽样方法,分别从总体中抽取一个容量为10,13,16,19的样本,分析样本容量与样本的平均数和标准差对总体的估计效果之间有什么关系.
20.为了解某市家庭用电量的情况,该市统计局调查了100户居民去年一年的月均用电量,发现他们的用电量都在50kW·h至350kW·h之间,进行适当分组后,画出频率分布直方图如图所示.
(I)求a的值;
(Ⅱ)求被调查用户中,用电量大于250kW·h的户数;
(III)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯定价,希望使80%的居民缴费在第一档(费用最低),请给出第一档用电标准(单位:kW·h)的建议,并简要说明理由.
21.一个经销鲜花产品的微店,为保障售出的百合花品质,每天从云南鲜花基地空运固定数量的百合花,如有剩余则免费分赠给第二天购花顾客,如果不足,则从本地鲜花供应商处进货.今年四月前10天,微店百合花的售价为每支2元,云南空运来的百合花每支进价1.6元,本地供应商处百合花每支进价1.8元,微店这10天的订单中百合花的需求量(单位:支)依次为:251,255,231,243,263,241,265,255,244,252.
(Ⅰ)求今年四月前10天订单中百合花需求量的平均数和众数,并完成频率分布直方图;
(Ⅱ)预计四月的后20天,订单中百合花需求量的频率分布与四月前10天相同,百合花进货价格与售价均不变,请根据(Ⅰ)中频率分布直方图判断(同一组中的需求量数据用该组区间的中点值作代表,位于各区间的频率代替位于该区间的概率),微店每天从云南固定空运250支,还是255支百合花,四月后20天百合花销售总利润会更大?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
根据五个矩形的面积和为1列式可得结果.
【详解】
由得.
故选:A
2.D
根据简单随机抽样的定义,即可求解,
【详解】
每个学生被抽到的可能性都是,
所以学号为01的同学被抽到的可能性为.
故选:D
3.C
利用分层抽样求出的值,进而可求得高三被抽取的人数.
【详解】
由分层抽样可得,可得,
设高三所抽取的人数为,则,解得.
故选:C.
4.C
利用中位数左右两边的小矩形的面积都等于即可求解.
【详解】
年龄位于的频率为,
年龄位于的频率为,
年龄位于的频率为,
年龄位于的频率为,
因为,而
,
所以中位数位于,设中位数为,
则,
解得:,
故选:C.
5.C
利用百分位数的定义求解即可
【详解】
,因为第6个和第7个数据分别为5.5和6.7,
所以估计这24户居民的月均用水量的第25百分位数为.
故选:C
6.B
根据演讲的人数,求得本次调查的人数为人,进而求得机器人所占的比例,即可求解.
【详解】
由题意,本次调查的人数为人,
其中合唱比赛所占的比例为,
所以机器人所占的比例为,
所以选取的学生中参加机器人社团的学生数为人.
故选:B.
7.C
先求出“史政生”所占的比例,然后按比例抽取人数,即可得到答案.
【详解】
由题意可知,“史政地”、“史政生”和“史地生”这三种组合的学生人数分别为210,90和60,
故“史政生”所占的比例为,
由分层抽样是按比例抽取可得,“史政生”组合中抽取的学生人数为.
故选:C
8.B
将样本数据由小到大进行排列,根据定义求出,即可得出结论.
【详解】
解:将生产的件数由小到大排列为:10、12、14、14、15、15、16、17、17、17,
∴ ,中位数为,
众数为,
因此,,
故选:B.
9.B
首先设原数据的平均数为,则新数据的平均数为,然后结合原数据的方差,利用方差的公式计算得出新数据的方差,再求出标准差即可.
【详解】
设原数据的平均数为,则新数据的平均数为,
则原数据的方差为,
则新数据的方差为:
.
故数据,,…,的标准差为:8.
故选:B.
10.C
根据平均数和方差的公式计算即可求解.
【详解】
设这个班有个学生,数据分别为,第个同学没有录入,
第一次计算时总分是,
方差是,
第二次计算时:,
方差
,
所以,,
故选:C.
11.D
先分别求出甲,乙,丙三名运动员射击成绩的平均分,然后根据方差公式求出相应的方差,比较大小可得标准差的大小.
【详解】
甲的平均成绩为,
其方差为
乙的平均成绩为,
其方差为丙的平均成绩为
其方差为.
所以
故选: D
12.A
根据百分位数的定义判断求解.
【详解】
因为,所以这组数据的第65百分位数是第6项数据4.5,
所以应有5个数不大于4.5,则,
故选:A.
13.
利用样本标准差的点估计值估计总体标准差的点估计值即可.
【详解】
解:由已知,样本的平均值为,
所以样本标准差的点估计值为
,
所以总体标准差的点估计值是,
故答案为:.
14..
根据所给数据依次找出前5个数即可.
【详解】
从表中第3行第4列开始向右读取数据,依次为:
所以得到的第5个样本编号是
故答案为:
15.
根据丙所带的钱的比例乘以总关税钱即得所求.
【详解】
依照钱的多少按比例出钱,
所以丙应该出钱为.
故答案为:.
16.
根据平均数、方差的性质计算可得;
【详解】
解:已知,则,
则
故答案为:
17.男生16人,女生12人
先计算得到抽取比例为,再计算得到答案.
【详解】
田径队运动员的总人数是,要得到28人的样本,占总体的比例为,
于是应该在男运动员中随机抽取(人),
在女运动员中随机抽取(人).
本题考查了分层抽样,属于简单题.
18.(1);(2);(3).
(1)由频率分布直方图的高之和为组距分之一,即可得出结果;
(2)根据样本容量、总体与频率之间的关系计算即可得出结果;
(3)用总面积1减去左边2个矩形的面积即可.
【详解】
解:(1)由频率分布直方图的性质得:
,
解得.
(2)∵成绩在的学生人数为6,
由频率分布直方图得成绩在的学生所占频率为:,
∴.
(3)根据样本估计“该校高一学生期末数学考试成绩70”的概率:
.
19.(1)平均数为199.75,总体标准差为95.26;(2)抓阄法;(3)(2)和(3)的计算结果不相同的概率相当大,而相同的概率很小;(4)由于样本的随机性,也有极个别(小概率)的例外情况.
(1)由平均数和方差公式计算;
(2)用抓阄法进行抽样;
(3)由于抽样的随机性,两种结果相同的概率很小,不同概率很大.
(4)由于样本容量增大,估计总体的精确程度会提高,效果更好(也有个别现象效果不好).
【详解】
(1)总体平均数为199.75.
总体标准差为95.26.
(2)可以使用抓阄法进行抽样.
(3)由样本的随机性,知(2)和(3)的计算结果不相同的概率相当大,而相同的概率很小.
(4)随着样本容量的增加,分别用样本平均数和样本标准差估计总体平均数和总体标准差的效果会越来越好(即精度会越来越高).但是由于样本的随机性,也有极个别(小概率)的例外情况.
本题考查用样本估计总体,样本容量越大时,估计效果可能会更好些.
20.(I);(Ⅱ);(III) kW·h.
(1)根据频率和为计算出的值;
(2)根据频率分布直方图计算出“用电量大于250kW·h”的频率,再将该频率乘以对应的总户数即可得到结果;
(3)根据频率分布直方图计算出频率刚好为时对应的月用电量,由此可得到第一档用电标准.
【详解】
(1)因为,所以;
(2)根据频率分布直方图可知:“用电量大于250kW·h”的频率为,
所以用电量大于250kW·h的户数为:,
故用电量大于250kW·h有户;
(3)因为前三组的频率和为:,
前四组的频率之和为,
所以频率为时对应的数据在第四组,
所以第一档用电标准为:kW·h.
故第一档用电标准为 kW·h.
本题考查频率分布直方图的综合应用,主要考查利用频率分布直方图进行相关计算,对学生读取图表信息和计算能力有一定要求,难度一般.
21.(Ⅰ)见解析(Ⅱ)四月后20天总利润更大
(Ⅰ)根据众数的定义直接可求出众为255.利用平均数的公式可以求出平均数.根据给定的分组,通过计算完成频率分布直方图.
(Ⅱ)设订单中百合花需求量为(支),由(Ⅰ)中频率分布直方图,可以求出可能取值、每个可能取值相应频率,每个可能取值相应的天数.分别求出空运250支, 255支百合花时,销售总利润的大小,进行比较,得出结论.
【详解】
解:(Ⅰ)四月前10天订单中百合需求量众数为255,
平均数
频率分布直方图补充如下:
(Ⅱ)设订单中百合花需求量为(支),由(Ⅰ)中频率分布直方图,
可能取值为235,245,255,265,相应频率分别为0.1,0.3,0.4,0.2,
∴20天中相应的天数为2天,6天,8天,4天.
①若空运250支
,当日利润为,
,当日利润为,
,当日利润为,
,当日利润为,
20天总利润为元.
②若空运255支
,当日利润为,
,当日利润为,
,当日利润为,
,当日利润为,
20天总利润为元.
∵,∴每天空运250支百合花四月后20天总利润更大.
本题考查了众数、平均数、频率分布直方图;重点考查了学生通过阅读,提取有用信息,用数学知识解决实际生活问题的能力.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
