1.4空间向量的应用 同步练习(Word版含解析)
文档属性
| 名称 | 1.4空间向量的应用 同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 11:50:40 | ||
图片预览




文档简介
人教A版(2019)选择性必修第一册 1.4 空间向量的应用 同步练习
一、单选题
1.已知平面、的法向量分别为、且,则的值为( )
A. B. C. D.
2.《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;鳖臑指的是四个面均为直角三角形的三棱锥如图,在堑堵ABC﹣A1B1C1中,∠ACB=90°,若AB=,AA1=2,当鳖臑A1﹣ABC体积最大时,直线B1C与平面ABB1A1所成角的余弦值为( )
A. B. C. D.
3.如图所示,已知点P为菱形ABCD所在平面外一点,且PA⊥平面ABCD,PA=AD=AC,点F为PC中点,则平面CBF与平面DBF夹角的正切值为( )
A. B.
C. D.
4.设直线的方向向量是,平面的法向量是,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.已知正四棱锥,侧棱长是底面边长的2倍,是的中点,则所成的角的余弦值为( )
A. B. C. D.
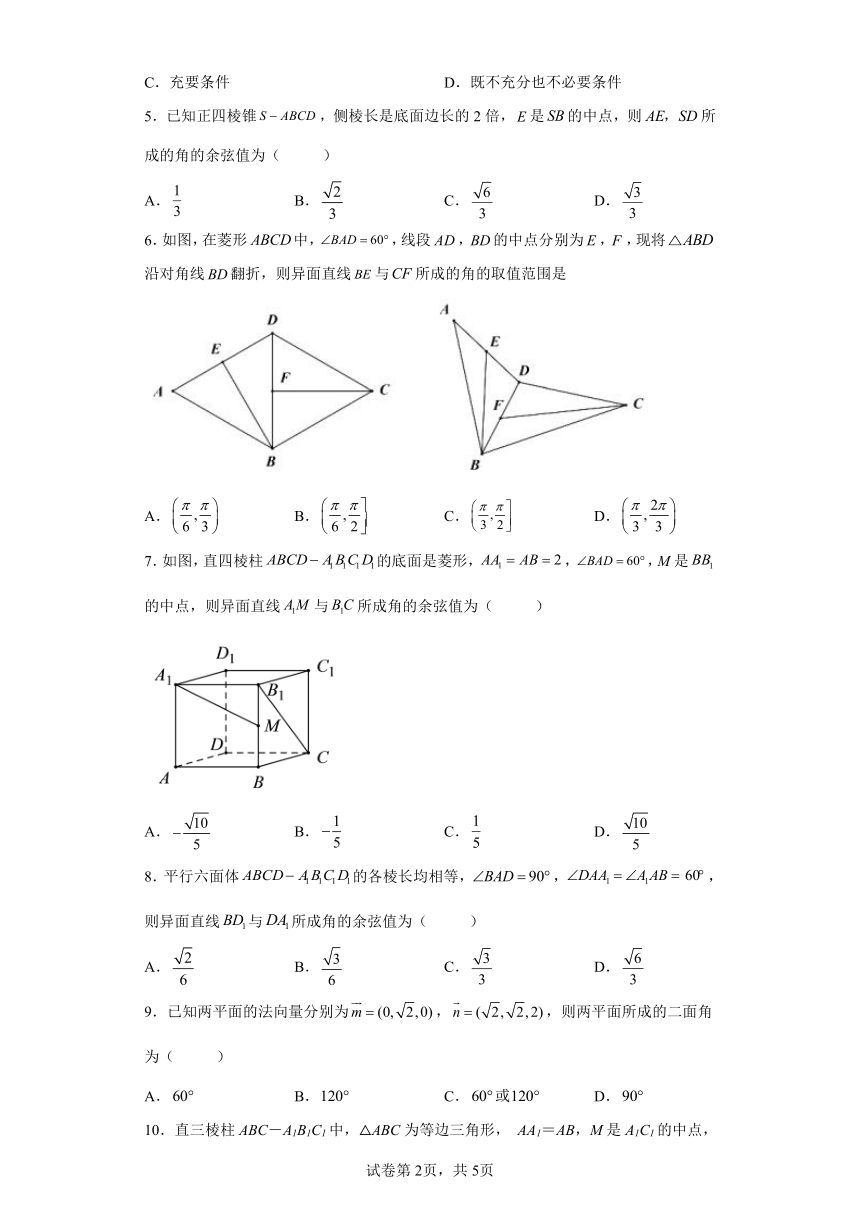
6.如图,在菱形中,,线段,的中点分别为,,现将沿对角线翻折,则异面直线与所成的角的取值范围是
A. B. C. D.
7.如图,直四棱柱的底面是菱形,,,M是的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
8.平行六面体的各棱长均相等,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
9.已知两平面的法向量分别为,,则两平面所成的二面角为( )
A. B. C.或 D.
10.直三棱柱ABC-A1B1C1中,△ABC为等边三角形, AA1=AB,M是A1C1的中点,则AM与平面所成角的正弦值为( )
A. B. C. D.
11.正三棱锥的侧面都是直角三角形,,分别是,的中点,则与平面所成角的正弦为( )
A. B. C. D.
12.如图,ABCD-EFGH是棱长为1的正方体,若P在正方体内部且满足,则P到AB的距离为( )
A. B.
C. D.
二、填空题
13.攒尖是古代中国建筑中屋顶的一种结构形式,依其平面有圆形攒尖、三角攒尖、四角攒尖、八角攒尖.如图属重檐四角攒尖,它的上层轮廓可近似看作一个正四棱锥,若此正四棱锥的侧面积是底面积的2倍,则侧面与底面的夹角为___________.
14.已知四面体ABCD中,AB,BC,BD两两垂直,,AB与平面ACD所成角的正切值为,则点B到平面ACD的距离为______.
15.在空间直角坐标系O-xyz中,已知点,,,异面直线与所成角的余弦值为___________.
16.正三棱柱中,,E为棱的中点,F为线段上一点,且,则_____.
17.已知向量为平面的法向量,点在内,则点到平面的距离为________________
三、解答题
18.如图,四棱锥的底面是矩形,底面,,,M为的中点.
(1)求证:;
(2)求平面与平面所成的角的余弦值.
19.如图,内接于,为的直径,,,,且平面,为的中点.
(1)求证:平面平面;
(2)求异面直线与所成的角;
(3)求点到平面的距离.
20.如图,四棱锥中,,,,,,.
(1)求证:;
(2)求直线与平面所成角的正弦值.
21.已知四边形是边长为的正方形,为等边三角形(如图所示),沿着折起到的位置,且使平面平面,是棱的中点(如图所示).
(1)求证:;
(2)求直线与平面所成角的余弦值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
利用两平面垂直,其法向量数量积为零列方程求解即可.
【详解】
因为平面、的法向量分别为、且,
所以,即,
则,
故选:A.
2.A
当鳖臑A1﹣ABC体积最大时,AC=BC=1,以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,由此能求出直线B1C与平面ABB1A1所成角的余弦值.
【详解】
解:在堑堵ABC﹣A1B1C1中,∠ACB=90°,AB=,AA1=2,当鳖臑A1﹣ABC体积最大时,AC=BC=1,
以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,
B1(0,1,2),C(0,0,0),A(1,0,0),B(0,1,0),
设平面ABB1A1的法向量,
则,取x=1,得,
设直线B1C与平面ABB1A1所成角为θ,
则,
所以
∴直线B1C与平面ABB1A1所成角的余弦值为.
故选:A.
3.D
设AC∩BD=O,连接OF,以O为原点,OB,OC,OF所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系,即可得出结果.
【详解】
设AC∩BD=O,连接OF,以O为原点,OB,OC,OF所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系,
设PA=AD=AC=1,则BD=,
∴且为平面BDF的一个法向量.
由,,
可得平面BCF的一个法向量为
.故选:D
4.B
根据线面平行的位置关系及直线的方向向量、平面的法向量定义再结合充分必要条件的定义判断即可.
【详解】
由,得:,则“”是“”的必要条件,
而不一定有,也可能,则“”不是“”的充分条件.
故选:B.
5.C
建立空间直角坐标系,利用空间向量法求出异面直线所成角的余弦值.
【详解】
解:如图所示建立空间直角坐标系,
不妨设,则,,所以
,,, ,, .
.
与所成角的余弦值为.
故选:.
6.C
设菱形的边长为1,则,利用向量的平行四边形法则得到,再利用数量积运算求出,再由 ,根据的范围,利用余弦函数的性质求解.
【详解】
设菱形的边长为1,则,
,
,
,
,
,
所以,
由图可知:,
所以,
所以,
所以,
所以异面直线与所成的角的取值范围是
故选:C
关键点点睛:本题关键是得到,转化为余弦函数求得其范围,进而求出的范围.
7.D
用向量分别表示,利用向量的夹角公式即可求解.
【详解】
由题意可得,
故选:D
本题主要考查用向量的夹角公式求异面直线所成的角,属于基础题.
8.B
利用基底向量表示出向量,,即可根据向量的夹角公式求出.
【详解】
如图所示:不妨设棱长为1,
,,
所以==,
,,
即,故异面直线与所成角的余弦值为.
故选:B.
9.C
由二面角的大小与二面角的两个半平面的法向量夹角的关系,求出法向量的夹角即可得解.
【详解】
因,所以.
因二面角的大小与二面角的两个半平面的法向量夹角相等或者互补,
所以两平面所成的二面角为或.
故选:C
10.B
取的中点,以为原点,所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,即可根据线面角的向量公式求出.
【详解】
如图所示,取的中点,以为原点,所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
不妨设,则,
所以,平面的一个法向量为
设AM与平面所成角为,向量与所成的角为,
所以,
即AM与平面所成角的正弦值为.
故选:B.
11.C
建立空间直角坐标系,求出相应点的坐标及平面平面PEF的法向量,代入即可得解.
【详解】
以点P为原点,PA为x轴,PB为y轴,PC为z轴,建立空间直角坐标系,如图所示,
设,则,
,
设平面PEF的法向量,
则,取得,
设平面与平面所成角为,则
故选:C
本题考查线面角的求法,建立适当坐标系用空间向量法进行求解,属于基础题.
12.C
以为坐标原点,AB,AD,AE所在直线分别为x,y,z轴建立空间直角坐标系, 由题意,计算出和的坐标,然后根据向量法求点到直线的距离公式即可求解.
【详解】
解:如图,以为坐标原点,AB,AD,AE所在直线分别为x,y,z轴建立空间直角坐标系,
则,,,
因为,
所以,,,
所以点P到AB的距离.
故选:C.
13.60°##π3
设此四棱锥P-ABCD底面边长为,斜高为,连结AC、BD交于点O,连结OP.则以O为原点,为x、y、z轴正半轴建立空间直角坐标系,用向量法求出侧面与底面的夹角.
【详解】
设此四棱锥P-ABCD底面边长为,斜高为,连结AC、BD交于点O,连结OP.则,,.
以O为原点,为x、y、z轴正半轴建立空间直角坐标系.
则,,
设平面的法向量为,
则,令,则,
显然平面的法向量为.
所以,
所以侧面与底面的夹角为.
故答案为:.
14.
取CD的中点E,连接AE,过B作交AE于F,可证得为AB与平面ACD所成的角,点B到平面ACD的距离为,计算可求得结果.
【详解】
如图,取CD的中点E,连接AE,过B作交AE于F.
,E是CD的中点,
,.
又平面ABE,
平面ABE.又平面ACD,
平面平面ACD.
又平面平面,,
平面ACD,故为AB与平面ACD所成的角.
,故.
又,
故答案为:
15.##
利用空间向量的数量积运算即可求解.
【详解】
解:因为,,,
所以,
设直线与所成角为,则
故答案为:.
16.15
建立空间直角坐标系,利用即求.
【详解】
如图建立空间直角坐标系,
则,,,设,
由知,
解得,
故.
故答案为:15.
17.
把点到平面距离问题转化为向量数量积问题求解.
【详解】
解:,0,,点到平面的距离为.
故答案为:.
18.(1)证明见解析;(2).
(1)以点D为原点,依次以DA,DC,DP所在直线为x,y,z轴建立空间直角坐标系,求出 ,利用数量积即可证明.
(2)求出两平面PAM与平面PDC的法向量,则法向量夹角余弦得二面角的余弦.
【详解】
解:(1)依题意,棱DA,DC,DP两两互相垂直.
以点D为原点,依次以DA,DC,DP所在直线为x,y,z轴,
如图,建立空间直角坐标系.
则,,,.
可得,.
所以,
所以
(2)由(1)得到,,
因此可得,.
设平面的一个法向量为,则由
得
令,解得.
同理,可求平面PDC的一个法向量.
所以,平面PAM与平面PDC所成的锐二面角满足:
.
即平面PAM与平面PDC所成的锐二面角的余弦值为.
19.(1)证明见解析;
(2);
(3)﹒
(1)建立空间直角坐标系,利用向量法证得平面平面;
(2)利用向量法求得异面直线与所成的角;
(3)利用向量法求得点到平面的距离.
(1)
依题意是圆的直径,∴,
由于平面,∴,
以C为空间坐标原点建立如图所示空间直角坐标系:
,
设是平面的法向量,
则,故可取.
,
设是平面的法向量,
则,故可取,
,∴平面平面.
(2)
,
设直线与直线所成角为,
则;
(3)
,平面的法向量为,
∴平面,∴到平面的距离为.
20.(1)证明见解析;(2).
(1)先证平面,即可通过线面垂直推证线线垂直;
(2)建立空间直角坐标系,求得直线的方向向量以及平面的法向量,用向量法即可求得线面夹角.
【详解】
(1)如下图所示,取的中点,连接.
,,为的中点,则,,
又,可得,故四边形为平行四边形,,
且,,
,,,则,,
,,平面,
平面,因此,;
(2)以点为坐标原点,、所在直线分别为、轴
建立如下图所示的空间直角坐标系,
则点、、、,
所以,,,.
设平面的法向量为,
由,得,可得,
令,可得,,则,
.
因此,直线与平面所成角的正弦值为.
本题考查利用线面垂直证明线线垂直,以及用向量法求线面角,属综合基础题.
21.(1)证明见解析
(2)
(1)取的中点,过点作的平行线,根据面面垂直的性质可证得平面,则以为坐标原点可建立空间直角坐标系,根据两向量数量积为零可证得垂直关系;
(2)利用线面角的向量求法可求得线面角的正弦值,由同角三角函数关系得所求余弦值.
(1)
(1)证明:取的中点,连接,并过点作的平行线,交于,
则.
为正三角形,,
平面平面,平面平面,平面,
平面,又平面,.
以为坐标原点,以,,所在直线分别为轴,轴,轴建立如图所示的空间直角坐标系,
,则,,,,,,
,.
(2)
,,
设平面的一个法向量为,
则,即,令,解得:,,.
设直线与平面所成的角为,
则,
直线与平面所成角的余弦值为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知平面、的法向量分别为、且,则的值为( )
A. B. C. D.
2.《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;鳖臑指的是四个面均为直角三角形的三棱锥如图,在堑堵ABC﹣A1B1C1中,∠ACB=90°,若AB=,AA1=2,当鳖臑A1﹣ABC体积最大时,直线B1C与平面ABB1A1所成角的余弦值为( )
A. B. C. D.
3.如图所示,已知点P为菱形ABCD所在平面外一点,且PA⊥平面ABCD,PA=AD=AC,点F为PC中点,则平面CBF与平面DBF夹角的正切值为( )
A. B.
C. D.
4.设直线的方向向量是,平面的法向量是,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.已知正四棱锥,侧棱长是底面边长的2倍,是的中点,则所成的角的余弦值为( )
A. B. C. D.
6.如图,在菱形中,,线段,的中点分别为,,现将沿对角线翻折,则异面直线与所成的角的取值范围是
A. B. C. D.
7.如图,直四棱柱的底面是菱形,,,M是的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
8.平行六面体的各棱长均相等,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
9.已知两平面的法向量分别为,,则两平面所成的二面角为( )
A. B. C.或 D.
10.直三棱柱ABC-A1B1C1中,△ABC为等边三角形, AA1=AB,M是A1C1的中点,则AM与平面所成角的正弦值为( )
A. B. C. D.
11.正三棱锥的侧面都是直角三角形,,分别是,的中点,则与平面所成角的正弦为( )
A. B. C. D.
12.如图,ABCD-EFGH是棱长为1的正方体,若P在正方体内部且满足,则P到AB的距离为( )
A. B.
C. D.
二、填空题
13.攒尖是古代中国建筑中屋顶的一种结构形式,依其平面有圆形攒尖、三角攒尖、四角攒尖、八角攒尖.如图属重檐四角攒尖,它的上层轮廓可近似看作一个正四棱锥,若此正四棱锥的侧面积是底面积的2倍,则侧面与底面的夹角为___________.
14.已知四面体ABCD中,AB,BC,BD两两垂直,,AB与平面ACD所成角的正切值为,则点B到平面ACD的距离为______.
15.在空间直角坐标系O-xyz中,已知点,,,异面直线与所成角的余弦值为___________.
16.正三棱柱中,,E为棱的中点,F为线段上一点,且,则_____.
17.已知向量为平面的法向量,点在内,则点到平面的距离为________________
三、解答题
18.如图,四棱锥的底面是矩形,底面,,,M为的中点.
(1)求证:;
(2)求平面与平面所成的角的余弦值.
19.如图,内接于,为的直径,,,,且平面,为的中点.
(1)求证:平面平面;
(2)求异面直线与所成的角;
(3)求点到平面的距离.
20.如图,四棱锥中,,,,,,.
(1)求证:;
(2)求直线与平面所成角的正弦值.
21.已知四边形是边长为的正方形,为等边三角形(如图所示),沿着折起到的位置,且使平面平面,是棱的中点(如图所示).
(1)求证:;
(2)求直线与平面所成角的余弦值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
利用两平面垂直,其法向量数量积为零列方程求解即可.
【详解】
因为平面、的法向量分别为、且,
所以,即,
则,
故选:A.
2.A
当鳖臑A1﹣ABC体积最大时,AC=BC=1,以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,由此能求出直线B1C与平面ABB1A1所成角的余弦值.
【详解】
解:在堑堵ABC﹣A1B1C1中,∠ACB=90°,AB=,AA1=2,当鳖臑A1﹣ABC体积最大时,AC=BC=1,
以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,
B1(0,1,2),C(0,0,0),A(1,0,0),B(0,1,0),
设平面ABB1A1的法向量,
则,取x=1,得,
设直线B1C与平面ABB1A1所成角为θ,
则,
所以
∴直线B1C与平面ABB1A1所成角的余弦值为.
故选:A.
3.D
设AC∩BD=O,连接OF,以O为原点,OB,OC,OF所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系,即可得出结果.
【详解】
设AC∩BD=O,连接OF,以O为原点,OB,OC,OF所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系,
设PA=AD=AC=1,则BD=,
∴且为平面BDF的一个法向量.
由,,
可得平面BCF的一个法向量为
.故选:D
4.B
根据线面平行的位置关系及直线的方向向量、平面的法向量定义再结合充分必要条件的定义判断即可.
【详解】
由,得:,则“”是“”的必要条件,
而不一定有,也可能,则“”不是“”的充分条件.
故选:B.
5.C
建立空间直角坐标系,利用空间向量法求出异面直线所成角的余弦值.
【详解】
解:如图所示建立空间直角坐标系,
不妨设,则,,所以
,,, ,, .
.
与所成角的余弦值为.
故选:.
6.C
设菱形的边长为1,则,利用向量的平行四边形法则得到,再利用数量积运算求出,再由 ,根据的范围,利用余弦函数的性质求解.
【详解】
设菱形的边长为1,则,
,
,
,
,
,
所以,
由图可知:,
所以,
所以,
所以,
所以异面直线与所成的角的取值范围是
故选:C
关键点点睛:本题关键是得到,转化为余弦函数求得其范围,进而求出的范围.
7.D
用向量分别表示,利用向量的夹角公式即可求解.
【详解】
由题意可得,
故选:D
本题主要考查用向量的夹角公式求异面直线所成的角,属于基础题.
8.B
利用基底向量表示出向量,,即可根据向量的夹角公式求出.
【详解】
如图所示:不妨设棱长为1,
,,
所以==,
,,
即,故异面直线与所成角的余弦值为.
故选:B.
9.C
由二面角的大小与二面角的两个半平面的法向量夹角的关系,求出法向量的夹角即可得解.
【详解】
因,所以.
因二面角的大小与二面角的两个半平面的法向量夹角相等或者互补,
所以两平面所成的二面角为或.
故选:C
10.B
取的中点,以为原点,所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,即可根据线面角的向量公式求出.
【详解】
如图所示,取的中点,以为原点,所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
不妨设,则,
所以,平面的一个法向量为
设AM与平面所成角为,向量与所成的角为,
所以,
即AM与平面所成角的正弦值为.
故选:B.
11.C
建立空间直角坐标系,求出相应点的坐标及平面平面PEF的法向量,代入即可得解.
【详解】
以点P为原点,PA为x轴,PB为y轴,PC为z轴,建立空间直角坐标系,如图所示,
设,则,
,
设平面PEF的法向量,
则,取得,
设平面与平面所成角为,则
故选:C
本题考查线面角的求法,建立适当坐标系用空间向量法进行求解,属于基础题.
12.C
以为坐标原点,AB,AD,AE所在直线分别为x,y,z轴建立空间直角坐标系, 由题意,计算出和的坐标,然后根据向量法求点到直线的距离公式即可求解.
【详解】
解:如图,以为坐标原点,AB,AD,AE所在直线分别为x,y,z轴建立空间直角坐标系,
则,,,
因为,
所以,,,
所以点P到AB的距离.
故选:C.
13.60°##π3
设此四棱锥P-ABCD底面边长为,斜高为,连结AC、BD交于点O,连结OP.则以O为原点,为x、y、z轴正半轴建立空间直角坐标系,用向量法求出侧面与底面的夹角.
【详解】
设此四棱锥P-ABCD底面边长为,斜高为,连结AC、BD交于点O,连结OP.则,,.
以O为原点,为x、y、z轴正半轴建立空间直角坐标系.
则,,
设平面的法向量为,
则,令,则,
显然平面的法向量为.
所以,
所以侧面与底面的夹角为.
故答案为:.
14.
取CD的中点E,连接AE,过B作交AE于F,可证得为AB与平面ACD所成的角,点B到平面ACD的距离为,计算可求得结果.
【详解】
如图,取CD的中点E,连接AE,过B作交AE于F.
,E是CD的中点,
,.
又平面ABE,
平面ABE.又平面ACD,
平面平面ACD.
又平面平面,,
平面ACD,故为AB与平面ACD所成的角.
,故.
又,
故答案为:
15.##
利用空间向量的数量积运算即可求解.
【详解】
解:因为,,,
所以,
设直线与所成角为,则
故答案为:.
16.15
建立空间直角坐标系,利用即求.
【详解】
如图建立空间直角坐标系,
则,,,设,
由知,
解得,
故.
故答案为:15.
17.
把点到平面距离问题转化为向量数量积问题求解.
【详解】
解:,0,,点到平面的距离为.
故答案为:.
18.(1)证明见解析;(2).
(1)以点D为原点,依次以DA,DC,DP所在直线为x,y,z轴建立空间直角坐标系,求出 ,利用数量积即可证明.
(2)求出两平面PAM与平面PDC的法向量,则法向量夹角余弦得二面角的余弦.
【详解】
解:(1)依题意,棱DA,DC,DP两两互相垂直.
以点D为原点,依次以DA,DC,DP所在直线为x,y,z轴,
如图,建立空间直角坐标系.
则,,,.
可得,.
所以,
所以
(2)由(1)得到,,
因此可得,.
设平面的一个法向量为,则由
得
令,解得.
同理,可求平面PDC的一个法向量.
所以,平面PAM与平面PDC所成的锐二面角满足:
.
即平面PAM与平面PDC所成的锐二面角的余弦值为.
19.(1)证明见解析;
(2);
(3)﹒
(1)建立空间直角坐标系,利用向量法证得平面平面;
(2)利用向量法求得异面直线与所成的角;
(3)利用向量法求得点到平面的距离.
(1)
依题意是圆的直径,∴,
由于平面,∴,
以C为空间坐标原点建立如图所示空间直角坐标系:
,
设是平面的法向量,
则,故可取.
,
设是平面的法向量,
则,故可取,
,∴平面平面.
(2)
,
设直线与直线所成角为,
则;
(3)
,平面的法向量为,
∴平面,∴到平面的距离为.
20.(1)证明见解析;(2).
(1)先证平面,即可通过线面垂直推证线线垂直;
(2)建立空间直角坐标系,求得直线的方向向量以及平面的法向量,用向量法即可求得线面夹角.
【详解】
(1)如下图所示,取的中点,连接.
,,为的中点,则,,
又,可得,故四边形为平行四边形,,
且,,
,,,则,,
,,平面,
平面,因此,;
(2)以点为坐标原点,、所在直线分别为、轴
建立如下图所示的空间直角坐标系,
则点、、、,
所以,,,.
设平面的法向量为,
由,得,可得,
令,可得,,则,
.
因此,直线与平面所成角的正弦值为.
本题考查利用线面垂直证明线线垂直,以及用向量法求线面角,属综合基础题.
21.(1)证明见解析
(2)
(1)取的中点,过点作的平行线,根据面面垂直的性质可证得平面,则以为坐标原点可建立空间直角坐标系,根据两向量数量积为零可证得垂直关系;
(2)利用线面角的向量求法可求得线面角的正弦值,由同角三角函数关系得所求余弦值.
(1)
(1)证明:取的中点,连接,并过点作的平行线,交于,
则.
为正三角形,,
平面平面,平面平面,平面,
平面,又平面,.
以为坐标原点,以,,所在直线分别为轴,轴,轴建立如图所示的空间直角坐标系,
,则,,,,,,
,.
(2)
,,
设平面的一个法向量为,
则,即,令,解得:,,.
设直线与平面所成的角为,
则,
直线与平面所成角的余弦值为.
答案第1页,共2页
答案第1页,共2页
