20.1.1 第1课时 平均数 课件(共29张PPT)
文档属性
| 名称 | 20.1.1 第1课时 平均数 课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 12:14:35 | ||
图片预览







文档简介
(共29张PPT)
人教版八下数学
精品同步教学课件
20.1 数据的集中趋势
20.1.1第1课时 平均数
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
据资料记载,位于意大利的比萨斜塔1918-1958
这41年间,平均每年倾斜1.10毫米;1959-1969这11年
间,平均每年倾斜1.26毫米,
那么1918-1969这52年间,你
知道比萨斜塔平均每年倾斜
约多少毫米吗?(精确到
0.01毫米).
问题引入
平均数
1
问题1
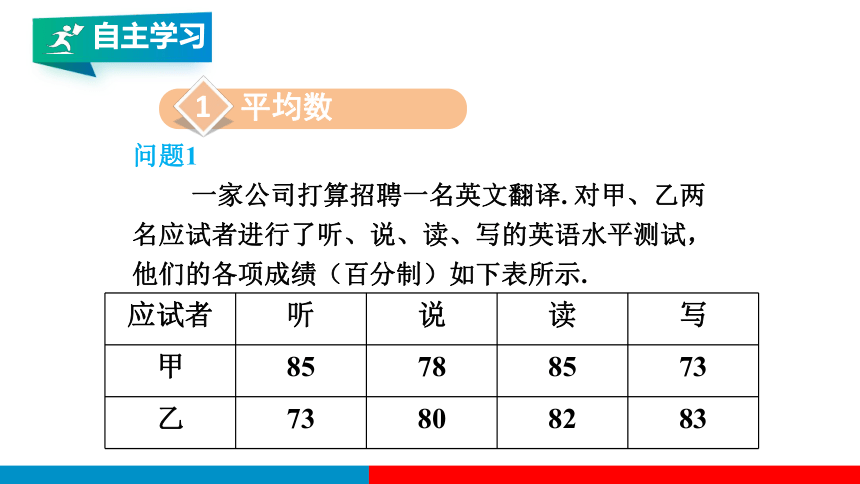
一家公司打算招聘一名英文翻译. 对甲、乙两
名应试者进行了听、说、读、写的英语水平测试,
他们的各项成绩(百分制)如下表所示.
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
自主学习
如果这家公司想招一名综合能力较强的翻译,
计算两名应试者的平均 成绩(百分制)从他们的成绩看,
应该录取谁?
对于上述问题,根据平均数公式,甲的平均成绩为
乙的平均成绩为
因为甲的平均成绩比乙高,所以应该录取甲.
自主学习
定义:一般地,对于n个数x1,x2,…,xn,我
们把 (x1+x2+…+xn)叫做这n个数的算术平
均数;
简称平均数;记为 ,读作:“x拔”.
自主学习
例 1
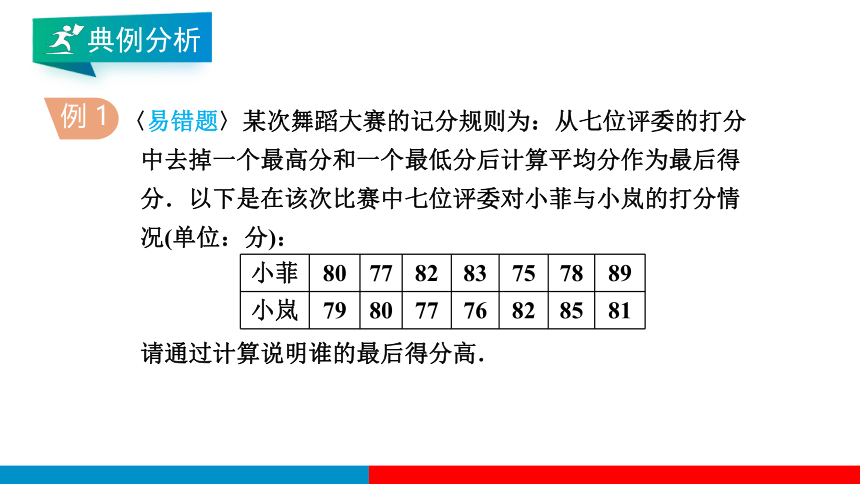
〈易错题〉某次舞蹈大赛的记分规则为:从七位评委的打分
中去掉一个最高分和一个最低分后计算平均分作为最后得
分.以下是在该次比赛中七位评委对小菲与小岚的打分情
况(单位:分):
请通过计算说明谁的最后得分高.
小菲 80 77 82 83 75 78 89
小岚 79 80 77 76 82 85 81
典例分析
导引:此题只需按照题中所给“记分规则”将两人的最后得分计算出
来,再进行大小比较即可.
解:小菲去掉一个最高分89分,去掉一个最低分75分,最后得分
为
典例分析
小岚去掉一个最高分85分,去掉一个最低分76分,
最后得分为
因为80分>79.8分,所以小菲的最后得分高.
典例分析
归 纳
当数据信息以表格或图象形式呈现时,要结合条
件读懂表格或图象,并从中获取有用的信息,本题去
掉一个最高分和一个最低分后,数据的个数也发生了
变化,计算平均得分时不要忘记这一点.求平均数要
牢记是数据总和除以数据总个数.
例2
在一次数学考试中,抽取了20名学生的试卷进行分析.这20
名学生的数学成绩(单位:分)分别为87,85,68,72,58,
100,93,97,96,83,51,84,92,62,83,79,74,72,
65,79[注:这份试卷满分100分,60分以上(含60分)者为合
格].求:
(1)这20名学生的平均成绩;
(2)这20名学生的合格率.
典例分析
导引:(1)观察所给的20个数据可以发现,这些数据都在80上下浮动,因此可将原数据都减去80,求得新数据的平均数,再加上80即为原数据的平均数,这样便于计算;(2)20名学生的合格率=
典例分析
解:(1)将原数据都减去80,得到新数据为7,5,-12,-8,
…,-15,-1.
所以新数据的平均数
(-15)+(-1)]÷20=-1(分).
所以原数据的平均数
即这20名学生的平均成绩为79分.
(2)这20名学生的合格率为
典例分析
1.
【中考·苏州】有一组数据:2,5,5,6,7,这组数据的平均数为( )
A.3 B.4 C.5 D.6
一组数据的和为87,平均数是3,则这组数据的个数为( )
A.87 B.3 C.29 D.90
C
C
2.
课堂练习
3.
已知一组数据a1,a2,a3,a4,a5的平均数为8,则另一组数据a1+10,a2-10,a3+10,a4-10,a5+10的平均数为( )
A.6 B.8
C.10 D.12
C
课堂练习
4.
已知数据x1,x2,x3,…,xn的平均数为m,则数据5x1,5x2,5x3,…,5xn的平均数为( )
A.m B.5m
C. D.10m
B
课堂练习
5.
已知一个班级有40人,数学老师第一次统计这个班的平均成绩为85分,在复查时发现漏记了一个学生的成绩80分,那么这个班的实际平均成绩应为( )
A.85分 B.84.875分
C.87分 D.84.5分
C
课堂练习
6.
【中考·深圳】已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是________.
8
课堂练习
例 3
算术平均数的应用
已知一组数据a1,a2,a3,a4,a5的平均数为8,则另一组数据a1+10,a2-10,a3+10,a4-10,a5+10的平均数为( )
A.6 B.8
C.10 D.12
C
典例分析
因为数据a1,a2,a3,a4,a5的平均数为8,所以a1+a2+a3+a4+a5=40. 又因为另一组数据a1+10,a2-10,a3+10,a4-10,a5+10的平均数为
(a1+10+a2-10+a3+10+a4-10+a5+10)=
×(a1+a2+a3+a4+a5+10)= ×(40+10)=10. 故应选C.
导引:
典例分析
加权平均数
2
定义:
(1)若n个数x1,x2,…,xn的权分别是w1,w2,…,
wn,则 叫做这n个数的加
权平均数;
自主学习
(2)在求n个数的平均数时,如果x1出现f1次,x2出现f2次,
…,xk出现fk次(这里f1+f2+…+fk=n),那么这n个
数的平均数 也叫做x1,x2,
…,xk这k个数的加权平均数,其中f1,f2,…,fk分
别叫做x1,x2,…,xk的权.
自主学习
例4
小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分
C.84.5分 D.86分
D
典例分析
导引:
把2,3,5分别看作是85分,80分和90分的权,按加权平均数的计算公式计算即可.
∵
∴小王的成绩为86分.
答案:D
典例分析
归 纳
权的形式有几种(比例、百分数、频(次)数),若以比例的形式为权,可直接将比例中的份数作为每个数的权进行计算.
1.
【中考·呼伦贝尔】从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )
A. B.
C. D.
B
课堂练均数
平均数的特点:
(1)一组数据的平均数是唯一的,它不一定是数据
中的某个数据;
(2)平均数是反映数据集中趋势的一个统计量,是
反映数据的平均水平的一个特征量;
(3)一般情况下,平均数能体现一组数据的整体性
质.
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版八下数学
精品同步教学课件
20.1 数据的集中趋势
20.1.1第1课时 平均数
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
据资料记载,位于意大利的比萨斜塔1918-1958
这41年间,平均每年倾斜1.10毫米;1959-1969这11年
间,平均每年倾斜1.26毫米,
那么1918-1969这52年间,你
知道比萨斜塔平均每年倾斜
约多少毫米吗?(精确到
0.01毫米).
问题引入
平均数
1
问题1
一家公司打算招聘一名英文翻译. 对甲、乙两
名应试者进行了听、说、读、写的英语水平测试,
他们的各项成绩(百分制)如下表所示.
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
自主学习
如果这家公司想招一名综合能力较强的翻译,
计算两名应试者的平均 成绩(百分制)从他们的成绩看,
应该录取谁?
对于上述问题,根据平均数公式,甲的平均成绩为
乙的平均成绩为
因为甲的平均成绩比乙高,所以应该录取甲.
自主学习
定义:一般地,对于n个数x1,x2,…,xn,我
们把 (x1+x2+…+xn)叫做这n个数的算术平
均数;
简称平均数;记为 ,读作:“x拔”.
自主学习
例 1
〈易错题〉某次舞蹈大赛的记分规则为:从七位评委的打分
中去掉一个最高分和一个最低分后计算平均分作为最后得
分.以下是在该次比赛中七位评委对小菲与小岚的打分情
况(单位:分):
请通过计算说明谁的最后得分高.
小菲 80 77 82 83 75 78 89
小岚 79 80 77 76 82 85 81
典例分析
导引:此题只需按照题中所给“记分规则”将两人的最后得分计算出
来,再进行大小比较即可.
解:小菲去掉一个最高分89分,去掉一个最低分75分,最后得分
为
典例分析
小岚去掉一个最高分85分,去掉一个最低分76分,
最后得分为
因为80分>79.8分,所以小菲的最后得分高.
典例分析
归 纳
当数据信息以表格或图象形式呈现时,要结合条
件读懂表格或图象,并从中获取有用的信息,本题去
掉一个最高分和一个最低分后,数据的个数也发生了
变化,计算平均得分时不要忘记这一点.求平均数要
牢记是数据总和除以数据总个数.
例2
在一次数学考试中,抽取了20名学生的试卷进行分析.这20
名学生的数学成绩(单位:分)分别为87,85,68,72,58,
100,93,97,96,83,51,84,92,62,83,79,74,72,
65,79[注:这份试卷满分100分,60分以上(含60分)者为合
格].求:
(1)这20名学生的平均成绩;
(2)这20名学生的合格率.
典例分析
导引:(1)观察所给的20个数据可以发现,这些数据都在80上下浮动,因此可将原数据都减去80,求得新数据的平均数,再加上80即为原数据的平均数,这样便于计算;(2)20名学生的合格率=
典例分析
解:(1)将原数据都减去80,得到新数据为7,5,-12,-8,
…,-15,-1.
所以新数据的平均数
(-15)+(-1)]÷20=-1(分).
所以原数据的平均数
即这20名学生的平均成绩为79分.
(2)这20名学生的合格率为
典例分析
1.
【中考·苏州】有一组数据:2,5,5,6,7,这组数据的平均数为( )
A.3 B.4 C.5 D.6
一组数据的和为87,平均数是3,则这组数据的个数为( )
A.87 B.3 C.29 D.90
C
C
2.
课堂练习
3.
已知一组数据a1,a2,a3,a4,a5的平均数为8,则另一组数据a1+10,a2-10,a3+10,a4-10,a5+10的平均数为( )
A.6 B.8
C.10 D.12
C
课堂练习
4.
已知数据x1,x2,x3,…,xn的平均数为m,则数据5x1,5x2,5x3,…,5xn的平均数为( )
A.m B.5m
C. D.10m
B
课堂练习
5.
已知一个班级有40人,数学老师第一次统计这个班的平均成绩为85分,在复查时发现漏记了一个学生的成绩80分,那么这个班的实际平均成绩应为( )
A.85分 B.84.875分
C.87分 D.84.5分
C
课堂练习
6.
【中考·深圳】已知一组数据x1,x2,x3,x4的平均数是5,则数据x1+3,x2+3,x3+3,x4+3的平均数是________.
8
课堂练习
例 3
算术平均数的应用
已知一组数据a1,a2,a3,a4,a5的平均数为8,则另一组数据a1+10,a2-10,a3+10,a4-10,a5+10的平均数为( )
A.6 B.8
C.10 D.12
C
典例分析
因为数据a1,a2,a3,a4,a5的平均数为8,所以a1+a2+a3+a4+a5=40. 又因为另一组数据a1+10,a2-10,a3+10,a4-10,a5+10的平均数为
(a1+10+a2-10+a3+10+a4-10+a5+10)=
×(a1+a2+a3+a4+a5+10)= ×(40+10)=10. 故应选C.
导引:
典例分析
加权平均数
2
定义:
(1)若n个数x1,x2,…,xn的权分别是w1,w2,…,
wn,则 叫做这n个数的加
权平均数;
自主学习
(2)在求n个数的平均数时,如果x1出现f1次,x2出现f2次,
…,xk出现fk次(这里f1+f2+…+fk=n),那么这n个
数的平均数 也叫做x1,x2,
…,xk这k个数的加权平均数,其中f1,f2,…,fk分
别叫做x1,x2,…,xk的权.
自主学习
例4
小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分
C.84.5分 D.86分
D
典例分析
导引:
把2,3,5分别看作是85分,80分和90分的权,按加权平均数的计算公式计算即可.
∵
∴小王的成绩为86分.
答案:D
典例分析
归 纳
权的形式有几种(比例、百分数、频(次)数),若以比例的形式为权,可直接将比例中的份数作为每个数的权进行计算.
1.
【中考·呼伦贝尔】从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )
A. B.
C. D.
B
课堂练均数
平均数的特点:
(1)一组数据的平均数是唯一的,它不一定是数据
中的某个数据;
(2)平均数是反映数据集中趋势的一个统计量,是
反映数据的平均水平的一个特征量;
(3)一般情况下,平均数能体现一组数据的整体性
质.
课堂小结
https://www.21cnjy.com/help/help_extract.php
