第七章随机变量及其分布 单元练习(Word版含解析)
文档属性
| 名称 | 第七章随机变量及其分布 单元练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 573.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 14:06:43 | ||
图片预览




文档简介
人教A版(2019)选择性必修第三册 第七章 随机变量及其分布 同步练习
一、单选题
1.设某医院仓库中有10盒同样规格的X光片,已知其中有5 盒、3盒、2盒依次是甲厂、乙厂、丙厂生产的.且甲、乙、丙三厂生产该种X光片的次品率依次为,现从这10盒中任取一盒,再从这盒中任取一张X光片,则取得的X光片是次品的概率为( )
A.0.08 B.0.1 C.0.15 D.0.2
2.有一批种子的发芽率为0.9,出芽后的幼苗成活率为0.8.在这批种子中,随机抽取一粒,则这粒种子能成长为幼苗的概率是( )
A.0.72 B.0.8
C.0.86 D.0.9
3.2020年1月,教育部出台《关于在部分高校开展基础学科招生改革试点工作的意见》(简称“强基计划”),明确从2020年起强基计划取代原有的高校自主招生方式.如果甲、乙、丙三人通过强基计划的概率分别为,那么三人中恰有两人通过的概率为( )
A. B. C. D.
4.已知下表为离散型随机变量X的分布列,则( )
X 0 1 2 3
P
A. B.
C. D.
5.将三颗骰子各掷一次,设事件为“三个点数全不相同”,事件为“三个点数不全相同”,则概率的值为
A. B. C. D.
6.有甲、乙两个盒子,甲盒子里有个红球,乙盒子里有个红球和个黑球,现从乙盒子里随机取出个球放入甲盒子后,再从甲盒子里随机取一球,记取到的红球个数为个,则随着的增加,下列说法正确的是( )
A.增加,增加 B.增加,减小
C.减小,增加 D.减小,减小
7.一道考题有4个答案,要求学生将其中的一个正确答案选择出来.某考生知道正确答案的概率为,在乱猜时,4个答案都有机会被他选择,若他答对了,则他确实知道正确答案的概率是( )
A. B. C. D.
8.已知随机变量的分布列如下:
1 1.5 2
则的最大值为( )A. B. C. D.
9.盒中有10个零件,其中8个是合格品,2个是不合格品,不放回地抽取2次,每次抽1个.已知第一次抽出的是合格品,则第二次抽出的是合格品的概率是( )
A. B. C. D.
10.有一批同一型号的产品,已知其中由一厂生产的占30%,二厂生产的占50%,三厂生产的占20%.又知这三个厂的产品次品率分别为2%,1%,1%,则从这批产品中任取一件是次品的概率是( )
A.0.013 B.0.04 C.0.002 D.0.003
11.某人射击一发子弹的命中率为,现他射击19发子弹,理论和实践都表明,这19发子弹中命中目标的子弹数n的概率如下表,那么在他射击完19发子弹后,其中击中目标的子弹数最大可能是( )
n 0 1 … k … 19
… …
A.14发 B.15发 C.16发 D.15或16发
12.有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球,甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( )
A.甲与丙相互独立 B.甲与丁相互独立
C.乙与丙相互独立 D.丙与丁相互独立
二、填空题
13.春天即将来临,某学校开展以“拥抱春天,播种绿色”为主题的植物种植实践体验活动.已知某种盆栽植物每株成活的概率为,各株是否成活相互独立.该学校的某班随机领养了此种盆栽植物10株,设为其中成活的株数,若的方差,,则________.
14.一用户在打电话时忘记了最后3个号码,只记得最后3个数两两不同,且都大于5.于是他随机拨最后3个数(两两不同),设他拨到正确号码的次数为X,随机变量X的可能值有_____个.
15.小赵 小钱 小孙 小李到个景点旅游,每人只去一个景点,设事件A为“个人去的景点不相同”,事件为“小赵独自去一个景点”,则________.
16.若随机变量,则服从的正态分布为______(填序号).
①;②;③;④.
三、解答题
17.为发展业务,某调研组准备从国内个人口超过1000万的超大城市和8个人口低于100万的小城市中随机抽取若干个城市,对其使用,两个公司开发的扫码支付软件的情况进行统计,若一次抽取2个城市,全是小城市的概率为.
(1)求的值;
(2)若一次抽取4个城市,
①假设抽取的小城市的个数为,求的分布列和期望;
②假设抽取的4个城市是同一类城市,求全为超大城市的概率.
18.已知10道试题中有4道选择题,甲、乙两人依次不放回地抽取1道,求:
(1)甲抽到选择题的概率;
(2)在甲抽到选择题的情况下,乙抽到选择题的概率.
19.天文学上用星等表示星体亮度,星等的数值越小,星体越亮.视星等是指观测者用肉眼所看到的星体亮度;绝对星等是假定把恒星放在距地球光年的地方测得的恒星的亮度,反映恒星的真实发光本领.下表列出了(除太阳外)视星等数值最小的10颗最亮恒星的相关数据,其中.
星名 天狼星 老人星 南门二 大角星 织女一 五车二 参宿七 南河三 水委一 参宿四
视星等 0.03 0.08 0.12 0.38 0.46 a
绝时星等 1.42 4.4 0.6 0.1 2.67
赤纬
(1)从表中随机选择一颗恒星,求它的绝对星等的数值小于视星等的数值的概率;
(2)已知北京的纬度是北纬,当且仅当一颗恒星的“赤纬”数值大于时,能在北京的夜空中看到它.现从这10颗恒星中随机选择4颗,记其中能在北京的夜空中看到的数量为颗,求的分布列和数学期望;
(3)记时10颗恒星的视星等的方差为,记时10颗恒星的视星等的方差为,判断与之间的大小关系.(结论不需要证明)
20.某牛奶店每天以每盒元的价格从牛奶厂购进若干盒鲜牛奶,然后以每盒元的价格出售,如果当天卖不完,剩下的牛奶作为垃圾回收处理.
(1)若牛奶店一天购进盒鲜牛奶,求当天的利润(单位:元)关于当天需求量(单位:盒,)的函数解析式;
(2)牛奶店老板记录了某天鲜牛奶的日需求量(单位:盒),整理得下表:
日需求量
频数
以这天记录的各需求量的频率作为各需求量发生的概率.
①若牛奶店一天购进盒鲜牛奶,表示当天的利润(单位:元),求的分布列及均值;
②若牛奶店计划一天购进盒或盒鲜牛奶,从统计学角度分析,你认为应购进盒还是盒?请说明理由.
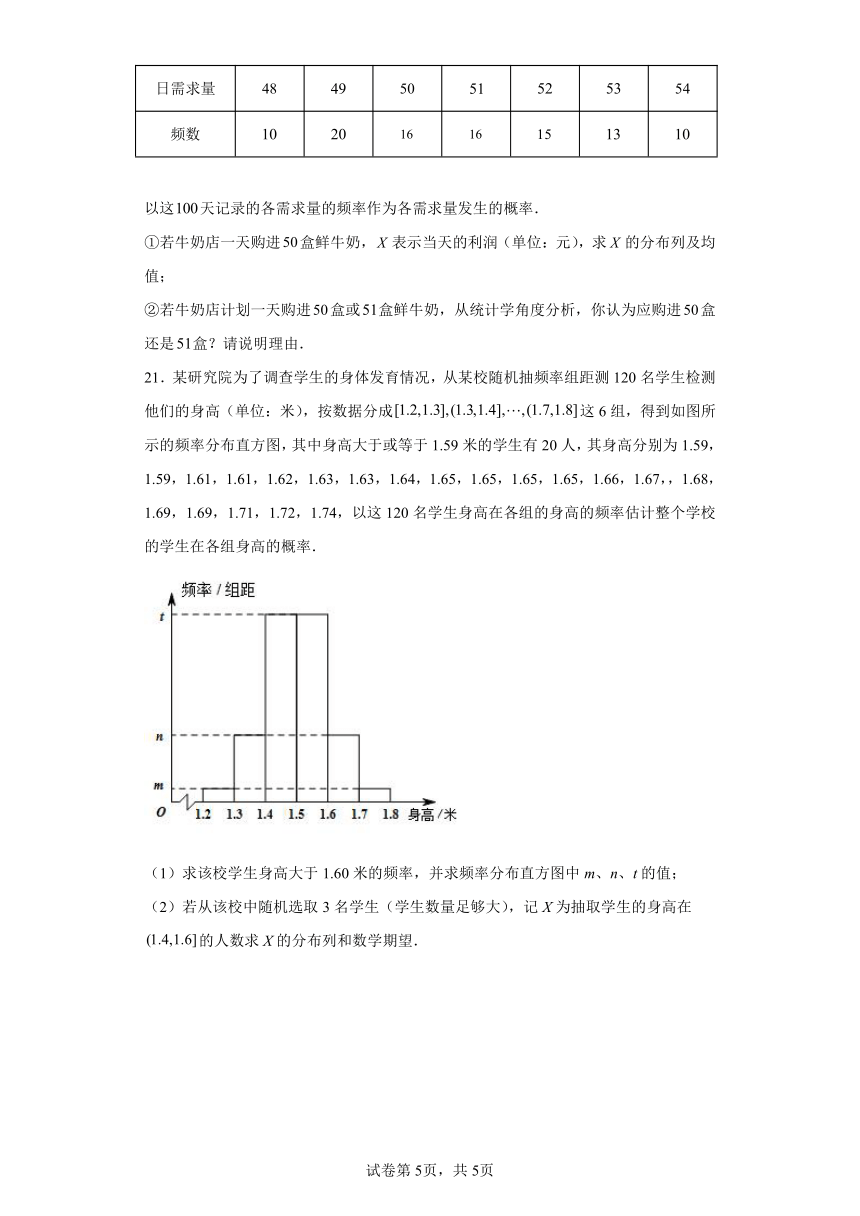
21.某研究院为了调查学生的身体发育情况,从某校随机抽频率组距测120名学生检测他们的身高(单位:米),按数据分成这6组,得到如图所示的频率分布直方图,其中身高大于或等于1.59米的学生有20人,其身高分别为1.59,1.59,1.61,1.61,1.62,1.63,1.63,1.64,1.65,1.65,1.65,1.65,1.66,1.67,,1.68,1.69,1.69,1.71,1.72,1.74,以这120名学生身高在各组的身高的频率估计整个学校的学生在各组身高的概率.
(1)求该校学生身高大于1.60米的频率,并求频率分布直方图中m、n、t的值;
(2)若从该校中随机选取3名学生(学生数量足够大),记X为抽取学生的身高在的人数求X的分布列和数学期望.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
利用条件概率公式即可求解.
【详解】
以A1,A2,A3分别表示取得的这盒X光片是由甲厂、乙厂、丙厂生产的,
B表示取得的X光片为次品,
P=,P=,P=,
P=,P=,P=;
则由全概率公式,
所求概率为P=P+P+P
=×+×+×=0.08.
故选:A
2.A
将所给数据代入条件概率公式计算而得.
【详解】
设“种子发芽”为事件A,“种子成长为幼苗”为事件AB(发芽,并成活而成长为幼苗),
则P(A)=0.9.又种子发芽后的幼苗成活率为P(B|A)=0.8,
所以P(AB)=P(A)·P(B|A)=0.9×0.8=0.72.
故选:A
3.C
根据积事件与和事件的概率公式可求解得到结果.
【详解】
记甲、乙、丙三人通过强基计划分别为事件,显然为相互独立事件,
则“三人中恰有两人通过”相当于事件,且互斥,
所求概率.
故选:C.
4.A
先利用分布列求得期望,进而得到方差求解.
【详解】
解:由题意得,
,
故.
故选:A.
5.D
根据条件概率的意义求解,先求出“三个点数不全相同”包含的所有情况数,在此范围内再求出“三个点数全不相同”包含的情况数,最后根据古典概型求解即可.
【详解】
由题意得表示在三个点数不全相同的条件下,三个点数全不相同的概率.
将三颗骰子各掷一次“三个点数不全相同”的情况有种,其中“三个点数全不相同”的情况有种,
所以所求概率为.
故选D.
条件概率的两种求法:
①利用定义,分别求和,得,这是通用的求条件概率的方法.
②借助古典概型概率公式,先求事件A包含的基本事件数,再在事件A发生的条件下求事件B包含的基本事件数,即,得.
6.C
由题意可知,从乙盒子里随机取出个球,含有红球个数服从超几何分布,即,可得出,再从甲盒子里随机取一球,则服从两点分布,所以,,从而可判断出和的增减性.
【详解】
由题意可知,从乙盒子里随机取出个球,含有红球个数服从超几何分布,即,其中,其中,且,.
故从甲盒中取球,相当于从含有个红球的个球中取一球,取到红球个数为.
故,
随机变量服从两点分布,所以,随着的增大,减小;
,随着的增大,增大.
故选:C.
本题考查超几何分布、两点分布,分布列与数学期望,考查推理能力与计算能力,属于难题.
7.B
利用全概率公式以及贝叶斯公式即可求解.
【详解】
设表示“考生答对”,表示“考生知道正确答案”,
由全概率公式得.
又由贝叶斯公式得.
故选:B
8.C
先根据概率分布列性质得,进而求得,再根据方差的计算公式得,最后结合二次函数性质即可得答案.
【详解】
解:有题得,即,所以,
故
,
因为,故,
所以由二次函数性质得,当,的最大值.
故选:C.
9.C
利用条件概率求解.
【详解】
设第一次抽到的是合格品为事件A,第二次抽到的是合格品为事件B,
则,
故选:C
10.A
设事件A为“任取一件为次品”,事件Bi为“任取一件为i厂的产品”,i=1,2,3,利用全概率公式P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+P(A|B3)·P(B3)即得解
【详解】
设事件A为“任取一件为次品”,
事件Bi为“任取一件为i厂的产品”,i=1,2,3,
则Ω=B1∪B2∪B3,且B1,B2,B3两两互斥,
易知P(B1)=0.3,P(B2)=0.5,P(B3)=0.2,P(A|B1)=0.02,P(A|B2)=0.01,P(A|B3)=0.01.
∴P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+P(A|B3)·P(B3)=0.02×0.3+0.01×0.5+0.01×0.2=0.013.
故选:A
11.D
设第k发子弹击中目标的概率最大,根据题意,可以表示第、k、发子弹击中目标的概率,进而可得且,即可得关于k的不等式组,求解可得答案.
【详解】
根据题意,设第k发子弹击中目标的概率最大,而19发子弹中命中目标的子弹数n的概率(,,,,),
则有且,
即 ,解可得 ,
即第15或16发子弹击中目标的可能性最大,
则他射完19发子弹后,击中目标的子弹最可能是第15或16发.
故选:D.
本题考查n次独立重复试验中发生k次的概率问题,考查逻辑思维能力和运算求解能力,属于常考题.
12.B
根据独立事件概率关系逐一判断
【详解】
,
故选:B
判断事件是否独立,先计算对应概率,再判断是否成立
13.
由题意可知:,且,从而可得值.
【详解】
由题意可知:
∴,即,
∴
故答案为:
本题考查二项分布的实际应用,考查分析问题解决问题的能力,考查计算能力,属于中档题.
14.
大于的数是,利用排列数计算出随机拨打的所有可能,由此得出所有可能取值的个数.
【详解】
大于的数是,一共有个,从中取出不同的三个进行排列,方法数有种.
本小题主要考查对离散型随机变量的理解,考查排列问题的识别以及排列数的计算,考查分析和解决问题的能力,属于基础题.题目关键点有两点,一个是记得的数都大于,这样的话可以确定出拨打的数为中的三个.由于电话号码是有顺序的差别的,故是排列问题,需要用排列数来计算出方法数.
15.
利用条件概率求解.
【详解】
小赵独自去一个景点共有种情况,即,
个人去的景点不同的情况有种,即,
所以.
故答案为:.
16.④
根据变量线性变化后,其均值、方差的变化情况判断.
【详解】
∵,,
∴,,故.故④正确.
故答案为:④
17.(1);(2)①分布列见解析,期望为;②.
(1)利用古典概型的概率计算公式列方程,由此求得.
(2)①利用超几何分布的分布列计算公式,计算出分布列并求得数学期望.
②利用古典概型的概率计算出所求的概率.
【详解】
(1)共个城市,抽取2个城市的方法种数是,其中全是小城市的情况种数为,
故全是小城市的概率是,
即,得.
(2)①由题意,知的可能取值为0,1,2,3,4.
;;;;.
故的分布列为
0 1 2 3 4
.
②若4个城市全是超大城市,共有种情况;
若4个城市全是小城市,共有种情况,
故全为超大城市的概率为.
18.(1)
(2)
(1)根据古典概型概率计算公式,计算出所求概率.
(2)根据古典概型概率计算公式,计算出所求概率.
(1)
甲抽到选择题的概率为
(2)
在甲抽到选择题的情况下,乙抽到选择题的概率为.
19.(1);(2)分布列见解析;数学期望为;(3).
(1)由图表数据可知有颗恒星绝对星等的数值小于视星等的数值,由古典概型概率公式可计算得到结果;
(2)首先确定所有可能取值,利用超几何分布概率公式计算可得每个取值对应的概率,由此可得分布列;根据数学期望计算公式可得期望;
(3)根据数据的波动程度可得方差大小关系.
【详解】
(1)设一颗星的绝对星等的数值小于视星等的数值为事件,
由图表可知:颗恒星有颗恒星绝对星等的数值小于视星等的数值.
.
(2)由图表知,有颗恒星的“赤纬”数值大于,有颗恒星的“赤纬”数值小于,则随机变量的所有可能取值为:,,,.
,,,.
随机变量的分布列为:
.
(3)结论:.
理由:当时,视星等的平均数为;当时,视星等的平均数为;可知当时,视星等的数值更集中在平均数附近,由此可知其方差更小.
关键点点睛:本题第二问考查了服从于超几何分布的随机变量的分布列与数学期望的求解,关键是能够确定随机变量服从于超几何分布,进而利用超几何分布概率公式计算得到每个取值对应的概率.
20.(1);(2)①分布列见解析,均值为;②每天购进盒比较合理,理由见解析.
(1)分、两种情况分析,结合题意可得出关于的函数关系式;
(2)①分析可知随机变量的可能取值有、、,结合表格计算出随机变量在不同取值下的概率,可得出随机变量的分布列,进一步可求得的值;
②设每天购进盒时,该牛奶店所获利润的数学期望值,与的值比较大小,即可得出结论.
【详解】
(1)当时,,
当时,.
所以,函数解析式为;
(2)①由(1)可知,当时,,当时,,当时,.
所以,随机变量的可能取值为、、,
,,,
所以,随机变量的分布列如下表所示:
;
②由①知当购进盒时,,
当购进盒时,,
设表示当天的利润,当时,,当时,,当时,,当时,,
,,,,
所以,,
因为,因此,每天购进盒比较合理.
21.(1) ,,;(2)分布列见详解;2.1.
(1)根据频率分布直方图中的对等关系,以及对应学生人数求解各参数值;
(2)学生的身高变量服从二项分布,故用二项分布公式求解即可.
【详解】
解:(1)由题意可知120名学生中身高大于1.60米的有18人,所以该校学生身高大于1.60米的频率为
记为学生身高,则
所以 ,,;
(2)由(1)知学生身高在 的概率
随机变量服从二项分布
则
所以的分布列为
0 1 2 3
0.027 0.189 0.441 0.343
第二问关键在判断变量服从二项分布,容易写出分布列.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.设某医院仓库中有10盒同样规格的X光片,已知其中有5 盒、3盒、2盒依次是甲厂、乙厂、丙厂生产的.且甲、乙、丙三厂生产该种X光片的次品率依次为,现从这10盒中任取一盒,再从这盒中任取一张X光片,则取得的X光片是次品的概率为( )
A.0.08 B.0.1 C.0.15 D.0.2
2.有一批种子的发芽率为0.9,出芽后的幼苗成活率为0.8.在这批种子中,随机抽取一粒,则这粒种子能成长为幼苗的概率是( )
A.0.72 B.0.8
C.0.86 D.0.9
3.2020年1月,教育部出台《关于在部分高校开展基础学科招生改革试点工作的意见》(简称“强基计划”),明确从2020年起强基计划取代原有的高校自主招生方式.如果甲、乙、丙三人通过强基计划的概率分别为,那么三人中恰有两人通过的概率为( )
A. B. C. D.
4.已知下表为离散型随机变量X的分布列,则( )
X 0 1 2 3
P
A. B.
C. D.
5.将三颗骰子各掷一次,设事件为“三个点数全不相同”,事件为“三个点数不全相同”,则概率的值为
A. B. C. D.
6.有甲、乙两个盒子,甲盒子里有个红球,乙盒子里有个红球和个黑球,现从乙盒子里随机取出个球放入甲盒子后,再从甲盒子里随机取一球,记取到的红球个数为个,则随着的增加,下列说法正确的是( )
A.增加,增加 B.增加,减小
C.减小,增加 D.减小,减小
7.一道考题有4个答案,要求学生将其中的一个正确答案选择出来.某考生知道正确答案的概率为,在乱猜时,4个答案都有机会被他选择,若他答对了,则他确实知道正确答案的概率是( )
A. B. C. D.
8.已知随机变量的分布列如下:
1 1.5 2
则的最大值为( )A. B. C. D.
9.盒中有10个零件,其中8个是合格品,2个是不合格品,不放回地抽取2次,每次抽1个.已知第一次抽出的是合格品,则第二次抽出的是合格品的概率是( )
A. B. C. D.
10.有一批同一型号的产品,已知其中由一厂生产的占30%,二厂生产的占50%,三厂生产的占20%.又知这三个厂的产品次品率分别为2%,1%,1%,则从这批产品中任取一件是次品的概率是( )
A.0.013 B.0.04 C.0.002 D.0.003
11.某人射击一发子弹的命中率为,现他射击19发子弹,理论和实践都表明,这19发子弹中命中目标的子弹数n的概率如下表,那么在他射击完19发子弹后,其中击中目标的子弹数最大可能是( )
n 0 1 … k … 19
… …
A.14发 B.15发 C.16发 D.15或16发
12.有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球,甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则( )
A.甲与丙相互独立 B.甲与丁相互独立
C.乙与丙相互独立 D.丙与丁相互独立
二、填空题
13.春天即将来临,某学校开展以“拥抱春天,播种绿色”为主题的植物种植实践体验活动.已知某种盆栽植物每株成活的概率为,各株是否成活相互独立.该学校的某班随机领养了此种盆栽植物10株,设为其中成活的株数,若的方差,,则________.
14.一用户在打电话时忘记了最后3个号码,只记得最后3个数两两不同,且都大于5.于是他随机拨最后3个数(两两不同),设他拨到正确号码的次数为X,随机变量X的可能值有_____个.
15.小赵 小钱 小孙 小李到个景点旅游,每人只去一个景点,设事件A为“个人去的景点不相同”,事件为“小赵独自去一个景点”,则________.
16.若随机变量,则服从的正态分布为______(填序号).
①;②;③;④.
三、解答题
17.为发展业务,某调研组准备从国内个人口超过1000万的超大城市和8个人口低于100万的小城市中随机抽取若干个城市,对其使用,两个公司开发的扫码支付软件的情况进行统计,若一次抽取2个城市,全是小城市的概率为.
(1)求的值;
(2)若一次抽取4个城市,
①假设抽取的小城市的个数为,求的分布列和期望;
②假设抽取的4个城市是同一类城市,求全为超大城市的概率.
18.已知10道试题中有4道选择题,甲、乙两人依次不放回地抽取1道,求:
(1)甲抽到选择题的概率;
(2)在甲抽到选择题的情况下,乙抽到选择题的概率.
19.天文学上用星等表示星体亮度,星等的数值越小,星体越亮.视星等是指观测者用肉眼所看到的星体亮度;绝对星等是假定把恒星放在距地球光年的地方测得的恒星的亮度,反映恒星的真实发光本领.下表列出了(除太阳外)视星等数值最小的10颗最亮恒星的相关数据,其中.
星名 天狼星 老人星 南门二 大角星 织女一 五车二 参宿七 南河三 水委一 参宿四
视星等 0.03 0.08 0.12 0.38 0.46 a
绝时星等 1.42 4.4 0.6 0.1 2.67
赤纬
(1)从表中随机选择一颗恒星,求它的绝对星等的数值小于视星等的数值的概率;
(2)已知北京的纬度是北纬,当且仅当一颗恒星的“赤纬”数值大于时,能在北京的夜空中看到它.现从这10颗恒星中随机选择4颗,记其中能在北京的夜空中看到的数量为颗,求的分布列和数学期望;
(3)记时10颗恒星的视星等的方差为,记时10颗恒星的视星等的方差为,判断与之间的大小关系.(结论不需要证明)
20.某牛奶店每天以每盒元的价格从牛奶厂购进若干盒鲜牛奶,然后以每盒元的价格出售,如果当天卖不完,剩下的牛奶作为垃圾回收处理.
(1)若牛奶店一天购进盒鲜牛奶,求当天的利润(单位:元)关于当天需求量(单位:盒,)的函数解析式;
(2)牛奶店老板记录了某天鲜牛奶的日需求量(单位:盒),整理得下表:
日需求量
频数
以这天记录的各需求量的频率作为各需求量发生的概率.
①若牛奶店一天购进盒鲜牛奶,表示当天的利润(单位:元),求的分布列及均值;
②若牛奶店计划一天购进盒或盒鲜牛奶,从统计学角度分析,你认为应购进盒还是盒?请说明理由.
21.某研究院为了调查学生的身体发育情况,从某校随机抽频率组距测120名学生检测他们的身高(单位:米),按数据分成这6组,得到如图所示的频率分布直方图,其中身高大于或等于1.59米的学生有20人,其身高分别为1.59,1.59,1.61,1.61,1.62,1.63,1.63,1.64,1.65,1.65,1.65,1.65,1.66,1.67,,1.68,1.69,1.69,1.71,1.72,1.74,以这120名学生身高在各组的身高的频率估计整个学校的学生在各组身高的概率.
(1)求该校学生身高大于1.60米的频率,并求频率分布直方图中m、n、t的值;
(2)若从该校中随机选取3名学生(学生数量足够大),记X为抽取学生的身高在的人数求X的分布列和数学期望.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
利用条件概率公式即可求解.
【详解】
以A1,A2,A3分别表示取得的这盒X光片是由甲厂、乙厂、丙厂生产的,
B表示取得的X光片为次品,
P=,P=,P=,
P=,P=,P=;
则由全概率公式,
所求概率为P=P+P+P
=×+×+×=0.08.
故选:A
2.A
将所给数据代入条件概率公式计算而得.
【详解】
设“种子发芽”为事件A,“种子成长为幼苗”为事件AB(发芽,并成活而成长为幼苗),
则P(A)=0.9.又种子发芽后的幼苗成活率为P(B|A)=0.8,
所以P(AB)=P(A)·P(B|A)=0.9×0.8=0.72.
故选:A
3.C
根据积事件与和事件的概率公式可求解得到结果.
【详解】
记甲、乙、丙三人通过强基计划分别为事件,显然为相互独立事件,
则“三人中恰有两人通过”相当于事件,且互斥,
所求概率.
故选:C.
4.A
先利用分布列求得期望,进而得到方差求解.
【详解】
解:由题意得,
,
故.
故选:A.
5.D
根据条件概率的意义求解,先求出“三个点数不全相同”包含的所有情况数,在此范围内再求出“三个点数全不相同”包含的情况数,最后根据古典概型求解即可.
【详解】
由题意得表示在三个点数不全相同的条件下,三个点数全不相同的概率.
将三颗骰子各掷一次“三个点数不全相同”的情况有种,其中“三个点数全不相同”的情况有种,
所以所求概率为.
故选D.
条件概率的两种求法:
①利用定义,分别求和,得,这是通用的求条件概率的方法.
②借助古典概型概率公式,先求事件A包含的基本事件数,再在事件A发生的条件下求事件B包含的基本事件数,即,得.
6.C
由题意可知,从乙盒子里随机取出个球,含有红球个数服从超几何分布,即,可得出,再从甲盒子里随机取一球,则服从两点分布,所以,,从而可判断出和的增减性.
【详解】
由题意可知,从乙盒子里随机取出个球,含有红球个数服从超几何分布,即,其中,其中,且,.
故从甲盒中取球,相当于从含有个红球的个球中取一球,取到红球个数为.
故,
随机变量服从两点分布,所以,随着的增大,减小;
,随着的增大,增大.
故选:C.
本题考查超几何分布、两点分布,分布列与数学期望,考查推理能力与计算能力,属于难题.
7.B
利用全概率公式以及贝叶斯公式即可求解.
【详解】
设表示“考生答对”,表示“考生知道正确答案”,
由全概率公式得.
又由贝叶斯公式得.
故选:B
8.C
先根据概率分布列性质得,进而求得,再根据方差的计算公式得,最后结合二次函数性质即可得答案.
【详解】
解:有题得,即,所以,
故
,
因为,故,
所以由二次函数性质得,当,的最大值.
故选:C.
9.C
利用条件概率求解.
【详解】
设第一次抽到的是合格品为事件A,第二次抽到的是合格品为事件B,
则,
故选:C
10.A
设事件A为“任取一件为次品”,事件Bi为“任取一件为i厂的产品”,i=1,2,3,利用全概率公式P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+P(A|B3)·P(B3)即得解
【详解】
设事件A为“任取一件为次品”,
事件Bi为“任取一件为i厂的产品”,i=1,2,3,
则Ω=B1∪B2∪B3,且B1,B2,B3两两互斥,
易知P(B1)=0.3,P(B2)=0.5,P(B3)=0.2,P(A|B1)=0.02,P(A|B2)=0.01,P(A|B3)=0.01.
∴P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+P(A|B3)·P(B3)=0.02×0.3+0.01×0.5+0.01×0.2=0.013.
故选:A
11.D
设第k发子弹击中目标的概率最大,根据题意,可以表示第、k、发子弹击中目标的概率,进而可得且,即可得关于k的不等式组,求解可得答案.
【详解】
根据题意,设第k发子弹击中目标的概率最大,而19发子弹中命中目标的子弹数n的概率(,,,,),
则有且,
即 ,解可得 ,
即第15或16发子弹击中目标的可能性最大,
则他射完19发子弹后,击中目标的子弹最可能是第15或16发.
故选:D.
本题考查n次独立重复试验中发生k次的概率问题,考查逻辑思维能力和运算求解能力,属于常考题.
12.B
根据独立事件概率关系逐一判断
【详解】
,
故选:B
判断事件是否独立,先计算对应概率,再判断是否成立
13.
由题意可知:,且,从而可得值.
【详解】
由题意可知:
∴,即,
∴
故答案为:
本题考查二项分布的实际应用,考查分析问题解决问题的能力,考查计算能力,属于中档题.
14.
大于的数是,利用排列数计算出随机拨打的所有可能,由此得出所有可能取值的个数.
【详解】
大于的数是,一共有个,从中取出不同的三个进行排列,方法数有种.
本小题主要考查对离散型随机变量的理解,考查排列问题的识别以及排列数的计算,考查分析和解决问题的能力,属于基础题.题目关键点有两点,一个是记得的数都大于,这样的话可以确定出拨打的数为中的三个.由于电话号码是有顺序的差别的,故是排列问题,需要用排列数来计算出方法数.
15.
利用条件概率求解.
【详解】
小赵独自去一个景点共有种情况,即,
个人去的景点不同的情况有种,即,
所以.
故答案为:.
16.④
根据变量线性变化后,其均值、方差的变化情况判断.
【详解】
∵,,
∴,,故.故④正确.
故答案为:④
17.(1);(2)①分布列见解析,期望为;②.
(1)利用古典概型的概率计算公式列方程,由此求得.
(2)①利用超几何分布的分布列计算公式,计算出分布列并求得数学期望.
②利用古典概型的概率计算出所求的概率.
【详解】
(1)共个城市,抽取2个城市的方法种数是,其中全是小城市的情况种数为,
故全是小城市的概率是,
即,得.
(2)①由题意,知的可能取值为0,1,2,3,4.
;;;;.
故的分布列为
0 1 2 3 4
.
②若4个城市全是超大城市,共有种情况;
若4个城市全是小城市,共有种情况,
故全为超大城市的概率为.
18.(1)
(2)
(1)根据古典概型概率计算公式,计算出所求概率.
(2)根据古典概型概率计算公式,计算出所求概率.
(1)
甲抽到选择题的概率为
(2)
在甲抽到选择题的情况下,乙抽到选择题的概率为.
19.(1);(2)分布列见解析;数学期望为;(3).
(1)由图表数据可知有颗恒星绝对星等的数值小于视星等的数值,由古典概型概率公式可计算得到结果;
(2)首先确定所有可能取值,利用超几何分布概率公式计算可得每个取值对应的概率,由此可得分布列;根据数学期望计算公式可得期望;
(3)根据数据的波动程度可得方差大小关系.
【详解】
(1)设一颗星的绝对星等的数值小于视星等的数值为事件,
由图表可知:颗恒星有颗恒星绝对星等的数值小于视星等的数值.
.
(2)由图表知,有颗恒星的“赤纬”数值大于,有颗恒星的“赤纬”数值小于,则随机变量的所有可能取值为:,,,.
,,,.
随机变量的分布列为:
.
(3)结论:.
理由:当时,视星等的平均数为;当时,视星等的平均数为;可知当时,视星等的数值更集中在平均数附近,由此可知其方差更小.
关键点点睛:本题第二问考查了服从于超几何分布的随机变量的分布列与数学期望的求解,关键是能够确定随机变量服从于超几何分布,进而利用超几何分布概率公式计算得到每个取值对应的概率.
20.(1);(2)①分布列见解析,均值为;②每天购进盒比较合理,理由见解析.
(1)分、两种情况分析,结合题意可得出关于的函数关系式;
(2)①分析可知随机变量的可能取值有、、,结合表格计算出随机变量在不同取值下的概率,可得出随机变量的分布列,进一步可求得的值;
②设每天购进盒时,该牛奶店所获利润的数学期望值,与的值比较大小,即可得出结论.
【详解】
(1)当时,,
当时,.
所以,函数解析式为;
(2)①由(1)可知,当时,,当时,,当时,.
所以,随机变量的可能取值为、、,
,,,
所以,随机变量的分布列如下表所示:
;
②由①知当购进盒时,,
当购进盒时,,
设表示当天的利润,当时,,当时,,当时,,当时,,
,,,,
所以,,
因为,因此,每天购进盒比较合理.
21.(1) ,,;(2)分布列见详解;2.1.
(1)根据频率分布直方图中的对等关系,以及对应学生人数求解各参数值;
(2)学生的身高变量服从二项分布,故用二项分布公式求解即可.
【详解】
解:(1)由题意可知120名学生中身高大于1.60米的有18人,所以该校学生身高大于1.60米的频率为
记为学生身高,则
所以 ,,;
(2)由(1)知学生身高在 的概率
随机变量服从二项分布
则
所以的分布列为
0 1 2 3
0.027 0.189 0.441 0.343
第二问关键在判断变量服从二项分布,容易写出分布列.
答案第1页,共2页
答案第1页,共2页
