安徽省泗县双语中学2012-2013学年高二下学期第一次月考数学(文)试题
文档属性
| 名称 | 安徽省泗县双语中学2012-2013学年高二下学期第一次月考数学(文)试题 | 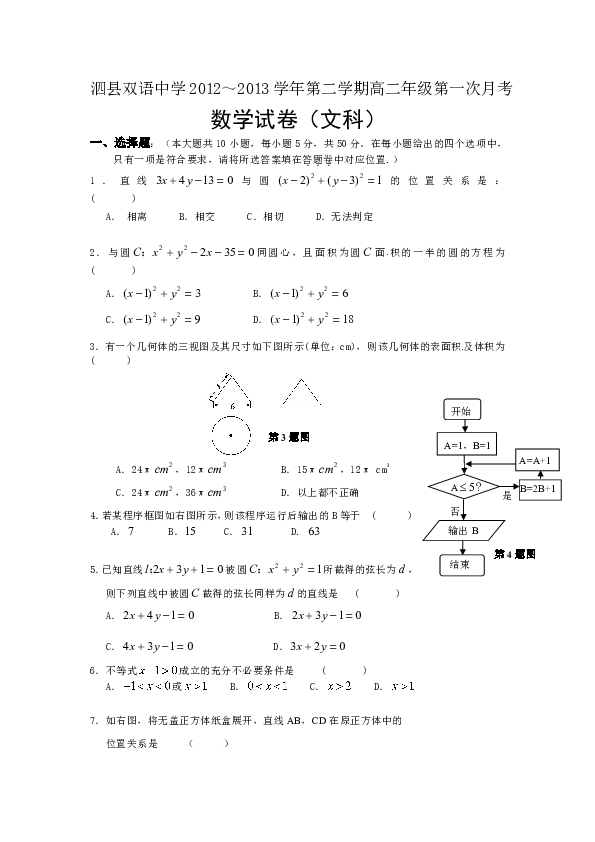 | |
| 格式 | zip | ||
| 文件大小 | 285.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-21 19:10:23 | ||
图片预览



文档简介
泗县双语中学2012~2013学年第二学期高二年级第一次月考
数学试卷(文科)
一、选择题:(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合要求,请将所选答案填在答题卷中对应位置.)
1.直线与圆的位置关系是: ( )
A. 相离 B.相交 C.相切 D.无法判定
2.与圆同圆心,且面积为圆面积的一半的圆的方程为 ( )
A. B.
C. D.
3.有一个几何体的三视图及其尺寸如下图所示(单位:cm),则该几何体的表面积及体积为 ( )
A.24π,12π B.15π,12π cm3
C.24π,36π D.以上都不正确
4.若某程序框图如右图所示,则该程序运行后输出的B等于 ( )
A. B. C. D.
5.已知直线被圆所截得的弦长为,
则下列直线中被圆截得的弦长同样为的直线是 ( )
A. B.
C. D.
6.不等式成立的充分不必要条件是 ( )
A.或 B. C. D.
7.如右图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的
位置关系是 ( )
A.平行 B.相交且垂直
C.异面 D.相交成60°
8.下列命题中,真命题是 ( )
A.空间不同三点确定一个平面
B.空间两两相交的三条直线确定一个平面
C.两组对边相等的四边形是平行四边形
D.和同一直线都相交的三条平行线在同一平面内
9.下图是2012年我校举办“激扬青春,勇担责任”演讲比赛大赛上,七位评委为某位选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的中位数和平均数分别为 ( )
A.85;87 B.84; 86 C.84;85 D.85;86
10.设表示平面,表示直线,给出下列四个命题:
①; ②;
③; ④。
其中正确命题的序号是 ( )
A.①② B.②④ C.③④ D.①③
二、填空题:(本题共5小题,每小题5分,共25分,把答案填在答题卷中对应题号后的横线上.)
11.命题:“设,若则”以及它的逆命题、否命题、逆否命题共四个命题中,真命题的个数为_____________.
12.将一枚均匀硬币先后抛两次,恰好有一次出现正面的概率为_____________.
13.为了解某社区居民有无收看“中央电视台2013年元旦联欢晚会”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么为______________.
14.以A(4,3,1),B(7,1,2),C(5,2,3)为顶点的三角形形状为?????????????三角形.
15.如右图,是直角三角形,,平面,
此图形中有 个直角三角形.
三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.)
16.(本小题12分)已知直线经过两点.
(Ⅰ)求直线的方程;
(Ⅱ)圆的圆心在直线上,并且与轴相切于点,求圆的方程.
17.(本小题12分)
已知圆,直线. (Ⅰ)当为何值时,直线与圆相切; (Ⅱ)当直线与圆相交于两点,且时,求直线的方程.
18.(本小题12分)
某种零件按质量标准分为五个等级.现从一批该零件中随机抽取个,对其等级进行统计分析,得到频率分布表如下:
等级
频率
(1)在抽取的个零件中,等级为的恰有个,求;
(2)在(1)的条件下,从等级为和的所有零件中,任意抽取个,求抽取的个零件等级恰好相同的概率.
19.(本小题13分)
设命题函数是减函数,命题:关于的不等式的解集为,如果“或”为真命题,“且”为假命题,求实数的取值范围.
20.(本小题12分)如下图, ,,
且,点为
的中点.
(Ⅰ) 求证:;
(Ⅱ) 求三棱锥的体积.
21.(本小题14分)如下图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
求证:(Ⅰ) PA//平面EDB;
(Ⅱ) PB⊥平面EFD.
三、解答题(共6小题,计75分。解答时,要有必要的文字说明、推导过程)
16. (本小题满分12分)
解:
(Ⅰ)直线的方程为:
(Ⅱ)设圆心为,
由于圆与轴相切于点,则,故圆心,
且半径为1,
则圆的方程为:
17. (本小题满分12分)
解: (1) 若直线与圆C相切,则有.解得.?
(2) 解:过圆心C作CD⊥AB,则根据题意和圆的性质,得 ?
解得. ∴直线的方程是和.
19. (本小题满分13分)
若命题:是减函数为真命题,则, 若命题:关于的不等式的解集为为真命题,则,则. 又∵“或”为真命题,“且”为假命题,
则,恰好一真一假 当命题为真命题,命题为假命题时, 当命题为假命题,命题为真命题时,, 故满足条件的实数的取值范围是.
21. (本小题满分14分)
证明:
(Ⅰ)连结AC,AC交BD于O.连结EO.
∵ 底面ABCD是正方形,∴ 点O是AC的中点.
在△PAC中,EO是中位线,∴ PA//EO.
而平面EDB,且平面EDB,
所以,PA//平面EDB.
(Ⅱ)∵ PD⊥底面ABCD,且底面ABCD,
∴ PD⊥DC.
∵ 底面ABCD是正方形,有DC⊥BC, ∴ BC⊥平面PDC.
而平面PDC,∴ BC⊥DE.
又∵PD=DC,E是PC的中点,∴ DE⊥PC.
∴ DE⊥平面PBC.
而平面PBC,∴ DE⊥PB.
又EF⊥PB,且,
所以PB⊥平面EFD.
数学试卷(文科)
一、选择题:(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合要求,请将所选答案填在答题卷中对应位置.)
1.直线与圆的位置关系是: ( )
A. 相离 B.相交 C.相切 D.无法判定
2.与圆同圆心,且面积为圆面积的一半的圆的方程为 ( )
A. B.
C. D.
3.有一个几何体的三视图及其尺寸如下图所示(单位:cm),则该几何体的表面积及体积为 ( )
A.24π,12π B.15π,12π cm3
C.24π,36π D.以上都不正确
4.若某程序框图如右图所示,则该程序运行后输出的B等于 ( )
A. B. C. D.
5.已知直线被圆所截得的弦长为,
则下列直线中被圆截得的弦长同样为的直线是 ( )
A. B.
C. D.
6.不等式成立的充分不必要条件是 ( )
A.或 B. C. D.
7.如右图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的
位置关系是 ( )
A.平行 B.相交且垂直
C.异面 D.相交成60°
8.下列命题中,真命题是 ( )
A.空间不同三点确定一个平面
B.空间两两相交的三条直线确定一个平面
C.两组对边相等的四边形是平行四边形
D.和同一直线都相交的三条平行线在同一平面内
9.下图是2012年我校举办“激扬青春,勇担责任”演讲比赛大赛上,七位评委为某位选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的中位数和平均数分别为 ( )
A.85;87 B.84; 86 C.84;85 D.85;86
10.设表示平面,表示直线,给出下列四个命题:
①; ②;
③; ④。
其中正确命题的序号是 ( )
A.①② B.②④ C.③④ D.①③
二、填空题:(本题共5小题,每小题5分,共25分,把答案填在答题卷中对应题号后的横线上.)
11.命题:“设,若则”以及它的逆命题、否命题、逆否命题共四个命题中,真命题的个数为_____________.
12.将一枚均匀硬币先后抛两次,恰好有一次出现正面的概率为_____________.
13.为了解某社区居民有无收看“中央电视台2013年元旦联欢晚会”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么为______________.
14.以A(4,3,1),B(7,1,2),C(5,2,3)为顶点的三角形形状为?????????????三角形.
15.如右图,是直角三角形,,平面,
此图形中有 个直角三角形.
三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.)
16.(本小题12分)已知直线经过两点.
(Ⅰ)求直线的方程;
(Ⅱ)圆的圆心在直线上,并且与轴相切于点,求圆的方程.
17.(本小题12分)
已知圆,直线. (Ⅰ)当为何值时,直线与圆相切; (Ⅱ)当直线与圆相交于两点,且时,求直线的方程.
18.(本小题12分)
某种零件按质量标准分为五个等级.现从一批该零件中随机抽取个,对其等级进行统计分析,得到频率分布表如下:
等级
频率
(1)在抽取的个零件中,等级为的恰有个,求;
(2)在(1)的条件下,从等级为和的所有零件中,任意抽取个,求抽取的个零件等级恰好相同的概率.
19.(本小题13分)
设命题函数是减函数,命题:关于的不等式的解集为,如果“或”为真命题,“且”为假命题,求实数的取值范围.
20.(本小题12分)如下图, ,,
且,点为
的中点.
(Ⅰ) 求证:;
(Ⅱ) 求三棱锥的体积.
21.(本小题14分)如下图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
求证:(Ⅰ) PA//平面EDB;
(Ⅱ) PB⊥平面EFD.
三、解答题(共6小题,计75分。解答时,要有必要的文字说明、推导过程)
16. (本小题满分12分)
解:
(Ⅰ)直线的方程为:
(Ⅱ)设圆心为,
由于圆与轴相切于点,则,故圆心,
且半径为1,
则圆的方程为:
17. (本小题满分12分)
解: (1) 若直线与圆C相切,则有.解得.?
(2) 解:过圆心C作CD⊥AB,则根据题意和圆的性质,得 ?
解得. ∴直线的方程是和.
19. (本小题满分13分)
若命题:是减函数为真命题,则, 若命题:关于的不等式的解集为为真命题,则,则. 又∵“或”为真命题,“且”为假命题,
则,恰好一真一假 当命题为真命题,命题为假命题时, 当命题为假命题,命题为真命题时,, 故满足条件的实数的取值范围是.
21. (本小题满分14分)
证明:
(Ⅰ)连结AC,AC交BD于O.连结EO.
∵ 底面ABCD是正方形,∴ 点O是AC的中点.
在△PAC中,EO是中位线,∴ PA//EO.
而平面EDB,且平面EDB,
所以,PA//平面EDB.
(Ⅱ)∵ PD⊥底面ABCD,且底面ABCD,
∴ PD⊥DC.
∵ 底面ABCD是正方形,有DC⊥BC, ∴ BC⊥平面PDC.
而平面PDC,∴ BC⊥DE.
又∵PD=DC,E是PC的中点,∴ DE⊥PC.
∴ DE⊥平面PBC.
而平面PBC,∴ DE⊥PB.
又EF⊥PB,且,
所以PB⊥平面EFD.
同课章节目录
