安徽省泗县双语中学2012-2013学年高二下学期第一次月考数学(理)试题
文档属性
| 名称 | 安徽省泗县双语中学2012-2013学年高二下学期第一次月考数学(理)试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 374.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-21 00:00:00 | ||
图片预览



文档简介
泗县双语中学2012~2013学年第二学期高二年级第一次月考
数学试卷(理科)
一、选择题:(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合要求,请将所选答案填在答题卷中对应位置.)
1.直线与圆的位置关系是: ( )
A. 相离 B.相交 C.相切 D.无法判定
2.与圆同圆心,且面积为圆面积的一半的圆的方程为 ( )
A. B.
C. D.
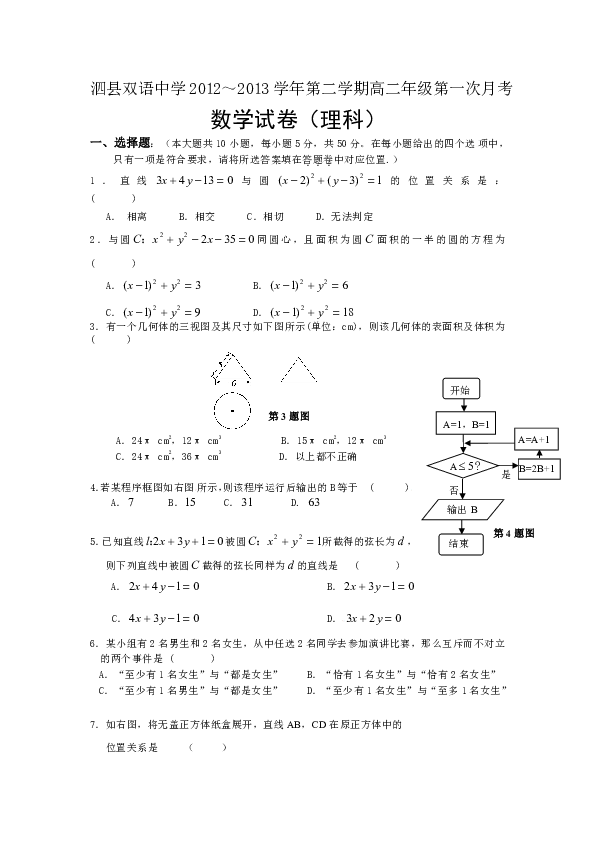
3.有一个几何体的三视图及其尺寸如下图所示(单位:cm),则该几何体的表面积及体积为 ( )
A.24π cm2,12π cm3 B.15π cm2,12π cm3
C.24π cm2,36π cm3 D.以上都不正确
4.若某程序框图如右图所示,则该程序运行后输出的B等于 ( )
A. B. C. D.
5.已知直线被圆所截得的弦长为,
则下列直线中被圆截得的弦长同样为的直线是 ( )
A. B.
C. D.
6.某小组有2名男生和2名女生,从中任选2名同学去参加演讲比赛,那么互斥而不对立的两个事件是 (??? )
A.“至少有1名女生”与“都是女生”
B.“恰有1名女生”与“恰有2名女生”
C.“至少有1名男生”与“都是女生”
D.“至少有1名女生”与“至多1名女生”
7.如右图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的
位置关系是 ( )
A.平行 B.相交且垂直
C.异面 D.相交成60°
8.下列命题中,真命题是 ( )
A.空间不同三点确定一个平面
B.空间两两相交的三条直线确定一个平面
C.两组对边相等的四边形是平行四边形
D.和同一直线都相交的三条平行线在同一平面内
9.下图是2012年我校举办“激扬青春,勇担责任”演讲比赛大赛上,七位评委为某位选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的中位数和平均数分别为 ( )
A.85;87 B.84; 86 C.84;85 D.85;86
10.已知空间四边形,其对角线为, 分别是
边的中点,点在线段上,且使,用
向量表示向量是????(????) A. B.
C. D.
二、填空题:(本题共5小题,每小题5分,共25分,把答案填在答题卷中对应题号后的横线上.)
11.将一枚均匀硬币先后抛两次,恰好有一次出现正面的概率为_____________.
12.为了解某社区居民有无收看“中央电视台2013年元旦联欢晚会”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么为______________.
13.以A(4,3,1),B(7,1,2),C(5,2,3)为顶点的三角形形状为?????????????三角形.
14.用1、2、3、4、5、6、7、8组成没有重复数字的八位数,要求1与2 相邻,3与4相邻,5与6相邻,而7与8不相邻,这样的八位数共有????? 个.(用数字作答)
15.设表示平面,表示直线,给出下列四个命题:
①; ②;
③; ④。
其中正确命题的序号是
三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.)
16.(本小题12分)
已知圆,直线. (Ⅰ)当为何值时,直线与圆相切; (Ⅱ)当直线与圆相交于两点,且时,求直线的方程.
17.(本小题12分)
某学校对学生的考试成绩作抽样调查,得到成绩的频率分布直方图如图所示,其中[70,80)对应的数值被污损,记为。
(Ⅰ)求的值;
(Ⅱ)记[90,100]为组,[80,90)为组,[70,80)为组,用分层抽样的办法从[90,100],[80,90),[70,80)三个分数段的学生中抽出6人参加比赛,从中任选3人为正选队员,求正选队员中有A组学生的概率。
18.(本小题13分)
设定点,动点在圆上运动,线段的中点为点. (Ⅰ)求的中点的轨迹方程;
(Ⅱ)直线与点的轨迹相切,且在轴、轴上的截距相等,求直线的方程.
19.(本小题12分)
如下图,在四面体中,,点分别是 的中点.
求证:(Ⅰ)直线∥平面;
(Ⅱ)平面平面.
20.(本小题13分)
如下图,在四棱锥中,底面是正方形,侧棱底面,,是的中点,作交于点.
求证:(Ⅰ)//平面;
(Ⅱ)⊥平面.
20.(本小题13分)
如图所示,在棱长为2的正方体中,、分别为、的中点.
(Ⅰ)求证://平面;
(Ⅱ)求三棱锥的体积;
(Ⅲ)求二面角的大小.
三、解答题(共6小题,计75分。解答时,要有必要的文字说明、推导过程)
16. (本小题满分12分)
解: (1) 若直线与圆C相切,则有.解得.?
(2) 解:过圆心C作CD⊥AB,则根据题意和圆的性质,得
?解得. 或 ∴直线的方程是和.
17. (本小题满分12分)
解:
(1)依题意知:=0.1-2×0.02-3×0.01=0.03
(2)由(1)知数比为0.01:0.02:0.03=1:2:3
故抽出的6人中A、B、C三组人数分别为1、2、3人。
从6人中抽选出3人的抽法有,其中3人中没有A组人的抽法有
故选出的3人中有A组人的概率
18. (本小题满分13分)
解:(1)设P点坐标为(),N点坐标为(),则由中点坐标公式有? N点在圆上
即为点P的轨迹方程? (2)因直线在轴、轴上截距相等,故的斜率存在且不为0,当直线在轴、轴 截距都为0时,设直线的方程为,即0 直线与相切 ????????? 当在轴、轴上的截距均不为0时,设直线的方程为,即 直线与相切 , 故直线的方程为或 综上可知的方程为:或或???????
20. (本小题满分13分)
21. (本小题满分13分)
(1)连结,在中,、分别为,的中点,则
∵EF为中位线
而面,面
面
(2)等腰直角三角形BCD中,F为BD中点
①
正方体
,
②
综合①②,且
即CF为高 ,
数学试卷(理科)
一、选择题:(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合要求,请将所选答案填在答题卷中对应位置.)
1.直线与圆的位置关系是: ( )
A. 相离 B.相交 C.相切 D.无法判定
2.与圆同圆心,且面积为圆面积的一半的圆的方程为 ( )
A. B.
C. D.
3.有一个几何体的三视图及其尺寸如下图所示(单位:cm),则该几何体的表面积及体积为 ( )
A.24π cm2,12π cm3 B.15π cm2,12π cm3
C.24π cm2,36π cm3 D.以上都不正确
4.若某程序框图如右图所示,则该程序运行后输出的B等于 ( )
A. B. C. D.
5.已知直线被圆所截得的弦长为,
则下列直线中被圆截得的弦长同样为的直线是 ( )
A. B.
C. D.
6.某小组有2名男生和2名女生,从中任选2名同学去参加演讲比赛,那么互斥而不对立的两个事件是 (??? )
A.“至少有1名女生”与“都是女生”
B.“恰有1名女生”与“恰有2名女生”
C.“至少有1名男生”与“都是女生”
D.“至少有1名女生”与“至多1名女生”
7.如右图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的
位置关系是 ( )
A.平行 B.相交且垂直
C.异面 D.相交成60°
8.下列命题中,真命题是 ( )
A.空间不同三点确定一个平面
B.空间两两相交的三条直线确定一个平面
C.两组对边相等的四边形是平行四边形
D.和同一直线都相交的三条平行线在同一平面内
9.下图是2012年我校举办“激扬青春,勇担责任”演讲比赛大赛上,七位评委为某位选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的中位数和平均数分别为 ( )
A.85;87 B.84; 86 C.84;85 D.85;86
10.已知空间四边形,其对角线为, 分别是
边的中点,点在线段上,且使,用
向量表示向量是????(????) A. B.
C. D.
二、填空题:(本题共5小题,每小题5分,共25分,把答案填在答题卷中对应题号后的横线上.)
11.将一枚均匀硬币先后抛两次,恰好有一次出现正面的概率为_____________.
12.为了解某社区居民有无收看“中央电视台2013年元旦联欢晚会”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么为______________.
13.以A(4,3,1),B(7,1,2),C(5,2,3)为顶点的三角形形状为?????????????三角形.
14.用1、2、3、4、5、6、7、8组成没有重复数字的八位数,要求1与2 相邻,3与4相邻,5与6相邻,而7与8不相邻,这样的八位数共有????? 个.(用数字作答)
15.设表示平面,表示直线,给出下列四个命题:
①; ②;
③; ④。
其中正确命题的序号是
三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.)
16.(本小题12分)
已知圆,直线. (Ⅰ)当为何值时,直线与圆相切; (Ⅱ)当直线与圆相交于两点,且时,求直线的方程.
17.(本小题12分)
某学校对学生的考试成绩作抽样调查,得到成绩的频率分布直方图如图所示,其中[70,80)对应的数值被污损,记为。
(Ⅰ)求的值;
(Ⅱ)记[90,100]为组,[80,90)为组,[70,80)为组,用分层抽样的办法从[90,100],[80,90),[70,80)三个分数段的学生中抽出6人参加比赛,从中任选3人为正选队员,求正选队员中有A组学生的概率。
18.(本小题13分)
设定点,动点在圆上运动,线段的中点为点. (Ⅰ)求的中点的轨迹方程;
(Ⅱ)直线与点的轨迹相切,且在轴、轴上的截距相等,求直线的方程.
19.(本小题12分)
如下图,在四面体中,,点分别是 的中点.
求证:(Ⅰ)直线∥平面;
(Ⅱ)平面平面.
20.(本小题13分)
如下图,在四棱锥中,底面是正方形,侧棱底面,,是的中点,作交于点.
求证:(Ⅰ)//平面;
(Ⅱ)⊥平面.
20.(本小题13分)
如图所示,在棱长为2的正方体中,、分别为、的中点.
(Ⅰ)求证://平面;
(Ⅱ)求三棱锥的体积;
(Ⅲ)求二面角的大小.
三、解答题(共6小题,计75分。解答时,要有必要的文字说明、推导过程)
16. (本小题满分12分)
解: (1) 若直线与圆C相切,则有.解得.?
(2) 解:过圆心C作CD⊥AB,则根据题意和圆的性质,得
?解得. 或 ∴直线的方程是和.
17. (本小题满分12分)
解:
(1)依题意知:=0.1-2×0.02-3×0.01=0.03
(2)由(1)知数比为0.01:0.02:0.03=1:2:3
故抽出的6人中A、B、C三组人数分别为1、2、3人。
从6人中抽选出3人的抽法有,其中3人中没有A组人的抽法有
故选出的3人中有A组人的概率
18. (本小题满分13分)
解:(1)设P点坐标为(),N点坐标为(),则由中点坐标公式有? N点在圆上
即为点P的轨迹方程? (2)因直线在轴、轴上截距相等,故的斜率存在且不为0,当直线在轴、轴 截距都为0时,设直线的方程为,即0 直线与相切 ????????? 当在轴、轴上的截距均不为0时,设直线的方程为,即 直线与相切 , 故直线的方程为或 综上可知的方程为:或或???????
20. (本小题满分13分)
21. (本小题满分13分)
(1)连结,在中,、分别为,的中点,则
∵EF为中位线
而面,面
面
(2)等腰直角三角形BCD中,F为BD中点
①
正方体
,
②
综合①②,且
即CF为高 ,
同课章节目录
