2.2.2用样本的数字特征估计总体的数字特征(上)
文档属性
| 名称 | 2.2.2用样本的数字特征估计总体的数字特征(上) |

|
|
| 格式 | zip | ||
| 文件大小 | 422.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-21 00:00:00 | ||
图片预览



文档简介
课件18张PPT。2.2.2用样本的数字特征
估计总体的数字特征(上)湖南省耒阳市振兴学校
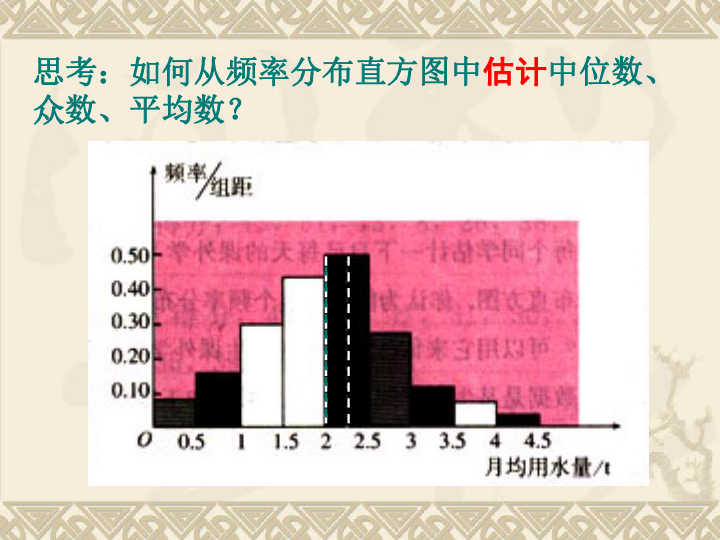
高中数学老师欧阳文丰制作思考:如何从频率分布直方图中估计中位数、众数、平均数? 一 、 众数、中位数、平均数与频率分布直方图的关系 1、众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。
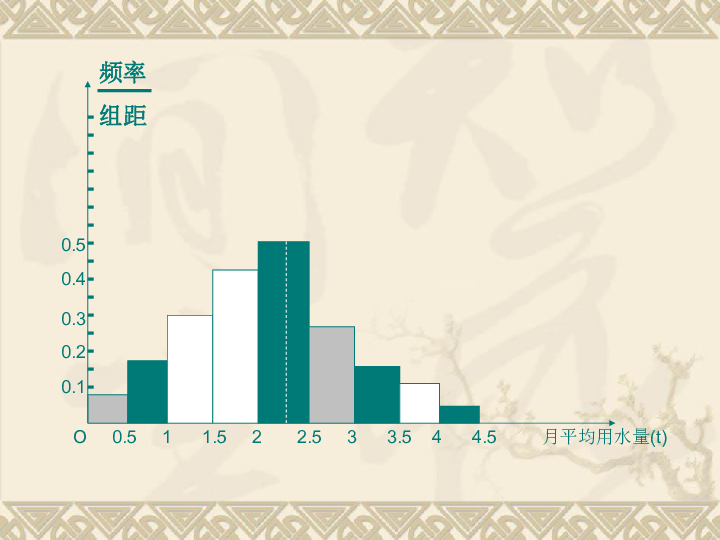
例如,在上一节调查的100位居民的月均用水量的问题中,从这些样本数据的频率分布直方图可以看出,月均用水量的众数是2.25t.如图所示:0.10.20.30.40.5O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t) 2、在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值。下图中虚线代表居民月均用水量的中位数的估计值,此数据值为2.02t. 0.10.20.30.40.5O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)说明:
2.02这个中位数的估计值,与样本的中位数值2.0不一样,这是因为样本数据的频率分布直方图,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致. 3、平均数是频率分布直方图的“重心”.
是直方图的平衡点. =每个分组的频率乘以分组中点之和0.10.20.30.40.5O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)小结众数、中位数、平均数与频率分布直方图的关系:1、众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。2、中位数左边和右边的直方图的面积应该相等,由取可估计中位数的值。3、平均数是直方图的“重心”(平衡点).二、2.02这个中位数的估计值,与样本的中位数值2.0不一样,你能解释其中的原因吗? 1、总体的各种数值特征都可以由两种途径来估计。
直接利用样本数据或由频率分布直方图来估计。
两种方法各有利弊;比如:(1)、通过频率分布直方图的估计精度低;(2)、通过频率分布直方图的估计结果与数据分组有关;(3)、在不能得到样本数据,只能得到频率分布直方图的情况下,也可以估计总体特征,而且直方图比较直观便于形象地进行分析。2、三种数字特征的优缺点 :(1)众数体现了样本数据的最大集中点,但它显然对其他数据信息的忽视使得无法客观地反映总体特征。(2)中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值不敏感有时也会成为缺点.(3)由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具有的性质。但平均数受数据中的极端值的影响较大,使平均数在估计总体时可靠性降低。 三、 众数、中位数、平均数的简单应用例 某工厂人员及工资构成如下:(1)指出这个问题中周工资的众数、中位数、平均数(2)这个问题中,工资的平均数能客观地反映该厂的工资水平吗?为什么? 分析:众数为200,中位数为220,平均数为300。
因平均数为300,由表格中所列出的数据可见,只有经理在平均数以上,其余的人都在平均数以下,故用平均数不能客观真实地反映该工厂的工资水平。四、阅读课本63页的思考,举例分析对极端值不敏感的利与弊。五、练习 应该采用平均数来表示每一个国家项目的平均金额,因为它能反映所有项目的信息。但平均数会受到极端数据2200万元的影响,所以大多数项目投资金额都和平均数相差比较大。归纳总结利用频率分布直方图估计样本的数字特征
(1)中位数:在频率分布直方图中,中位数左边和右边的直方图的面积______________,由此可以估计中位数的值.应该相等(2)平均数:平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的__________.
(3)众数:在频率分布直方图中,众数是最高的矩形的中点的___________.横坐标之和横坐标
例如,在上一节调查的100位居民的月均用水量的问题中,从这些样本数据的频率分布直方图可以看出,月均用水量的众数是2.25t.如图所示:0.10.20.30.40.5O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t) 2、在样本中,有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数,因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等,由此可以估计中位数的值。下图中虚线代表居民月均用水量的中位数的估计值,此数据值为2.02t. 0.10.20.30.40.5O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)说明:
2.02这个中位数的估计值,与样本的中位数值2.0不一样,这是因为样本数据的频率分布直方图,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致. 3、平均数是频率分布直方图的“重心”.
是直方图的平衡点. =每个分组的频率乘以分组中点之和0.10.20.30.40.5O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t)小结众数、中位数、平均数与频率分布直方图的关系:1、众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标。2、中位数左边和右边的直方图的面积应该相等,由取可估计中位数的值。3、平均数是直方图的“重心”(平衡点).二、2.02这个中位数的估计值,与样本的中位数值2.0不一样,你能解释其中的原因吗? 1、总体的各种数值特征都可以由两种途径来估计。
直接利用样本数据或由频率分布直方图来估计。
两种方法各有利弊;比如:(1)、通过频率分布直方图的估计精度低;(2)、通过频率分布直方图的估计结果与数据分组有关;(3)、在不能得到样本数据,只能得到频率分布直方图的情况下,也可以估计总体特征,而且直方图比较直观便于形象地进行分析。2、三种数字特征的优缺点 :(1)众数体现了样本数据的最大集中点,但它显然对其他数据信息的忽视使得无法客观地反映总体特征。(2)中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值不敏感有时也会成为缺点.(3)由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数都不具有的性质。但平均数受数据中的极端值的影响较大,使平均数在估计总体时可靠性降低。 三、 众数、中位数、平均数的简单应用例 某工厂人员及工资构成如下:(1)指出这个问题中周工资的众数、中位数、平均数(2)这个问题中,工资的平均数能客观地反映该厂的工资水平吗?为什么? 分析:众数为200,中位数为220,平均数为300。
因平均数为300,由表格中所列出的数据可见,只有经理在平均数以上,其余的人都在平均数以下,故用平均数不能客观真实地反映该工厂的工资水平。四、阅读课本63页的思考,举例分析对极端值不敏感的利与弊。五、练习 应该采用平均数来表示每一个国家项目的平均金额,因为它能反映所有项目的信息。但平均数会受到极端数据2200万元的影响,所以大多数项目投资金额都和平均数相差比较大。归纳总结利用频率分布直方图估计样本的数字特征
(1)中位数:在频率分布直方图中,中位数左边和右边的直方图的面积______________,由此可以估计中位数的值.应该相等(2)平均数:平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的__________.
(3)众数:在频率分布直方图中,众数是最高的矩形的中点的___________.横坐标之和横坐标
