平方根
图片预览




文档简介
课件25张PPT。
—人人学有价值的数学;
—人人都能获得必需的数学;
—不同的人在数学上得到不同发展;6.1.1 平方根猜 猜 如果一个数的平方等于9,这个数是几?
一个数的平方等于2呢?
想知道这个数的结果吗?
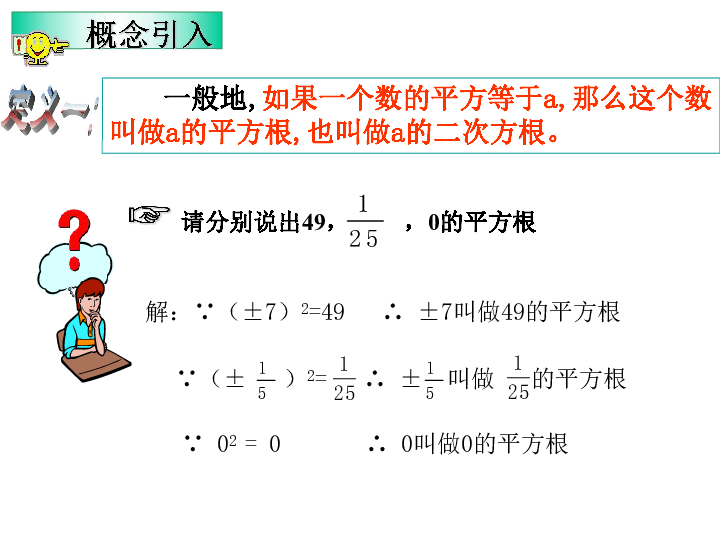
我们来学习——平方根 一般地,如果一个数的平方等于a,那么这个数
叫做a的平方根,也叫做a的二次方根。解:∵(±7)2=49 ∴ ±7叫做49的平方根∵(± )2= ∴ ± 叫做 的平方根∵ 02 = 0 ∴ 0叫做0的平方根概念引入 定义一:正的平方根用 来表示,(读做“根号a”)即:正数a的平方根表示为± (读做“正、负根号a” )如:49的平方根表示为 ,即 = ± 7
跟我学对于
正数a负的平方根用 “ ”表示(读做“负根号a” ),其中a叫做被开方数。那么,怎样表示一个数的平方根呢?一般地,如果一个数x的平方等于a,
那么这个数叫做a的平方根或二次方根。即:若x2=a,那么x叫做a的平方根。
记作:x=求一个数a的平方根的运算,叫做开平方。149+1-1+2-2+3-3149+1-1+2-2+3-3开平方平方开平方是平方的逆运算。规定:0的算术平方根是0. 一般地,如果一个正数x 的平方等于a, 即x2=a,那么这个正数x 叫做a的算术平方根. 概念完善、性质a的算术平方根记为
读作: “根号a”,a 叫做被开方数.1.双重非负性:①一个正数有两个平方根,这两个平方根互为相反数; ②0只有一个平方根,它就是0本身; ③负数没有平方根.平方根的性质:(1) ; (2) ; (3) ;
(4) ; (5) ; (6) .1.下列式子表示什么含义?你能求出它们的值吗?解:(1) 表示0.81 的算术平方根,
=0.9 (2) 表示25的算术平方根的相反数,
= -5问题1、是否所有的的算术平方根都
是正数?
那么我这句话怎么改就正确了规律一:所有的算术平方根
都是非负数问题2、是否所有的有理数都有算术
平方根?规律二、只有非负数才有算术平方根问题3、被开方数都是什么数?规律三、被开方数要求必须为非负数。你能举出几个平方根的例子吗???1416936254964811001211691962252562893243614001443. (1) 3的算术平方根是___.(2) 的算术平方根是___.⑶___ 算术平方根等于它本身.30和1⑷ 若 , 则42. 当x为何值时,下列各式有意义?
(1) ; (2) ;(3) ⑸若 ,则 64.已知 与 互为相反
数,求xy的算术平方根.判断:
(1)5是25的算术平方根; ( )
(2)-6是 36 的算术平方根; ( )
(3)0的算术平方根是0; ( )
(4)0.01是0.1的算术平方根; ( )
(5)-5是-25的算术平方根; ( )
(6)5的算术平方根是 。 ( )筛一筛,长能耐√×√√××拓展:已知 求x,y的值.解:根据题意得 和 均为非负数,所以 解方程组得, (1)你能否利用此折出面积为1的小正方形?(2)你能折出面积为2的小正方形吗?(3)折出面积为2的小正方形的边长为多少?游戏数学规定:0的算术平方根是0. 一般地,如果一个正数x 的平方等于a, 即x2=a,那么这个正数x 叫做a的算术平方根. a的算术平方根记为
读作: “根号a”,a 叫做被开方数.1.双重非负性:小结正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。a的一个平方根是3,则另一个平方根是 ,a= 。-393a-22和2a-3是m的两个平方根,
试求m的值。思考:1.下列各式哪些有意义,哪些没
有意义?
(1)- (2)
(3) (4)我们已学习了3种非负数,即绝对值、偶数次方、算术平方根。几个非负数的和为零,它们就同时为零,然后转化为方程(或方程组)来解。思考:你知道这个大正方形的边长是多少吗? 怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?探索 & 交流解:设这个大正方形的边长为x,则 x2=2x叫做2的算术平方根2的算术平方根记做:
一个数的平方等于2呢?
想知道这个数的结果吗?
我们来学习——平方根 一般地,如果一个数的平方等于a,那么这个数
叫做a的平方根,也叫做a的二次方根。解:∵(±7)2=49 ∴ ±7叫做49的平方根∵(± )2= ∴ ± 叫做 的平方根∵ 02 = 0 ∴ 0叫做0的平方根概念引入 定义一:正的平方根用 来表示,(读做“根号a”)即:正数a的平方根表示为± (读做“正、负根号a” )如:49的平方根表示为 ,即 = ± 7
跟我学对于
正数a负的平方根用 “ ”表示(读做“负根号a” ),其中a叫做被开方数。那么,怎样表示一个数的平方根呢?一般地,如果一个数x的平方等于a,
那么这个数叫做a的平方根或二次方根。即:若x2=a,那么x叫做a的平方根。
记作:x=求一个数a的平方根的运算,叫做开平方。149+1-1+2-2+3-3149+1-1+2-2+3-3开平方平方开平方是平方的逆运算。规定:0的算术平方根是0. 一般地,如果一个正数x 的平方等于a, 即x2=a,那么这个正数x 叫做a的算术平方根. 概念完善、性质a的算术平方根记为
读作: “根号a”,a 叫做被开方数.1.双重非负性:①一个正数有两个平方根,这两个平方根互为相反数; ②0只有一个平方根,它就是0本身; ③负数没有平方根.平方根的性质:(1) ; (2) ; (3) ;
(4) ; (5) ; (6) .1.下列式子表示什么含义?你能求出它们的值吗?解:(1) 表示0.81 的算术平方根,
=0.9 (2) 表示25的算术平方根的相反数,
= -5问题1、是否所有的的算术平方根都
是正数?
那么我这句话怎么改就正确了规律一:所有的算术平方根
都是非负数问题2、是否所有的有理数都有算术
平方根?规律二、只有非负数才有算术平方根问题3、被开方数都是什么数?规律三、被开方数要求必须为非负数。你能举出几个平方根的例子吗???1416936254964811001211691962252562893243614001443. (1) 3的算术平方根是___.(2) 的算术平方根是___.⑶___ 算术平方根等于它本身.30和1⑷ 若 , 则42. 当x为何值时,下列各式有意义?
(1) ; (2) ;(3) ⑸若 ,则 64.已知 与 互为相反
数,求xy的算术平方根.判断:
(1)5是25的算术平方根; ( )
(2)-6是 36 的算术平方根; ( )
(3)0的算术平方根是0; ( )
(4)0.01是0.1的算术平方根; ( )
(5)-5是-25的算术平方根; ( )
(6)5的算术平方根是 。 ( )筛一筛,长能耐√×√√××拓展:已知 求x,y的值.解:根据题意得 和 均为非负数,所以 解方程组得, (1)你能否利用此折出面积为1的小正方形?(2)你能折出面积为2的小正方形吗?(3)折出面积为2的小正方形的边长为多少?游戏数学规定:0的算术平方根是0. 一般地,如果一个正数x 的平方等于a, 即x2=a,那么这个正数x 叫做a的算术平方根. a的算术平方根记为
读作: “根号a”,a 叫做被开方数.1.双重非负性:小结正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。a的一个平方根是3,则另一个平方根是 ,a= 。-393a-22和2a-3是m的两个平方根,
试求m的值。思考:1.下列各式哪些有意义,哪些没
有意义?
(1)- (2)
(3) (4)我们已学习了3种非负数,即绝对值、偶数次方、算术平方根。几个非负数的和为零,它们就同时为零,然后转化为方程(或方程组)来解。思考:你知道这个大正方形的边长是多少吗? 怎样用两个面积为1的小正方形拼成一个面积为2的大正方形?探索 & 交流解:设这个大正方形的边长为x,则 x2=2x叫做2的算术平方根2的算术平方根记做:
