华师大版八下数学 18.5平行四边形 复习教案
文档属性
| 名称 | 华师大版八下数学 18.5平行四边形 复习教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 158.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 00:00:00 | ||
图片预览

文档简介
第18章 平行四边形 复习
【教学目标】
1、通过对几种平行四边形的回顾与思考,使学生梳理所学的知识,系统地复习平行四边形与各种特殊平行四边形的定义、性质、判定方法,三角形的中位线定理等;
2、正确理解平行四边形与各种特殊平行四边形的联系与区别,在反思和交流过程中,逐渐建立知识体系;
3、引导学生独立思考,通过归纳、概括、实践等系统数学活动,感受获得成功的体验,形成科学的学习习惯。
【教学重点】
1、平行四边形与各种特殊平行四边形的区别。
2、梳理平行四边形、矩形、菱形、正方形、三角形的中位线定理的知识体系及应用方法。
【教学难点】
平行四边形与各种特殊平行四边形的定义、性质、判定的综合运用。
【教学模式】
以题代纲,梳理知识-----变式训练,查漏补缺-----综合训练,总结规律-----测试练习,提高效率。
【教具准备】实物投影仪、电脑、自制课件。
【教学过程】
一、梳理知识 开门见山,直奔主题
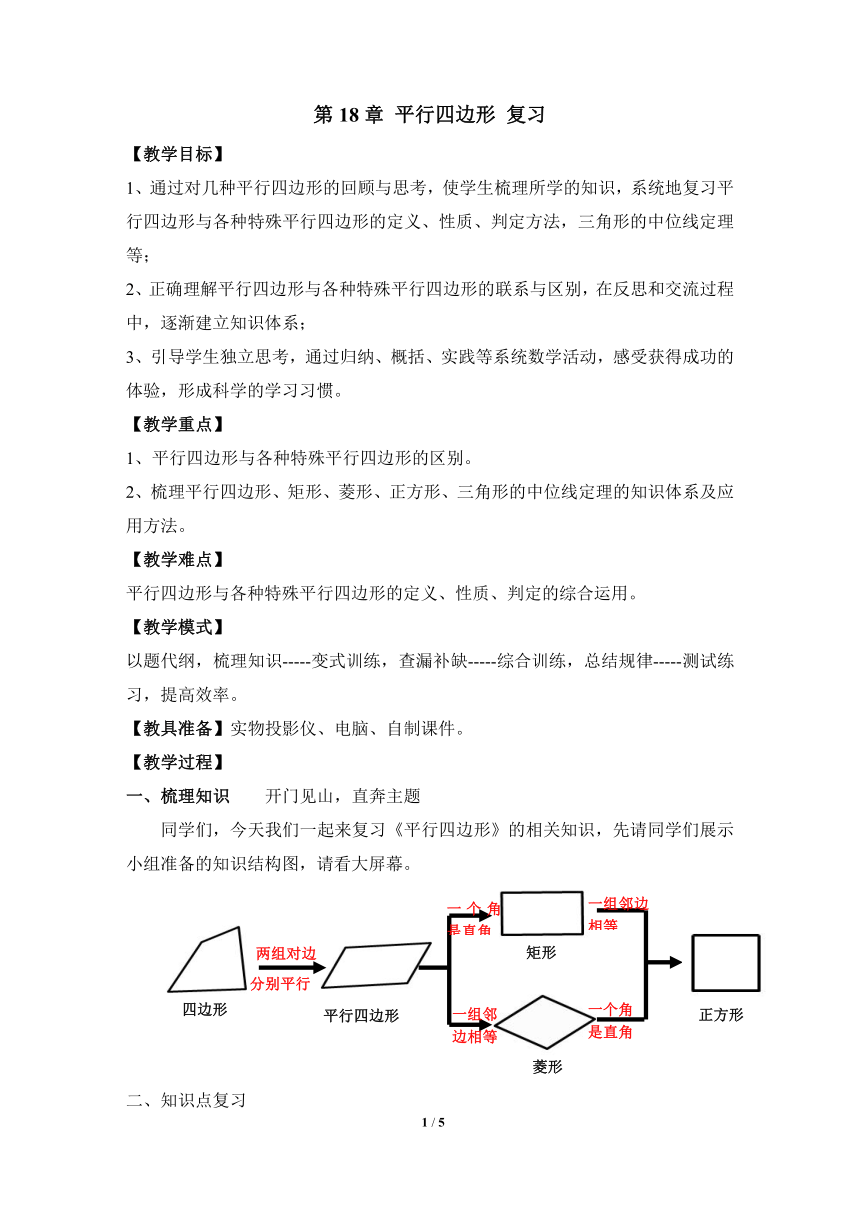
同学们,今天我们一起来复行四边形》的相关知识,先请同学们展示小组准备的知识结构图,请看大屏幕。
二、知识点复习
活动一(性质)
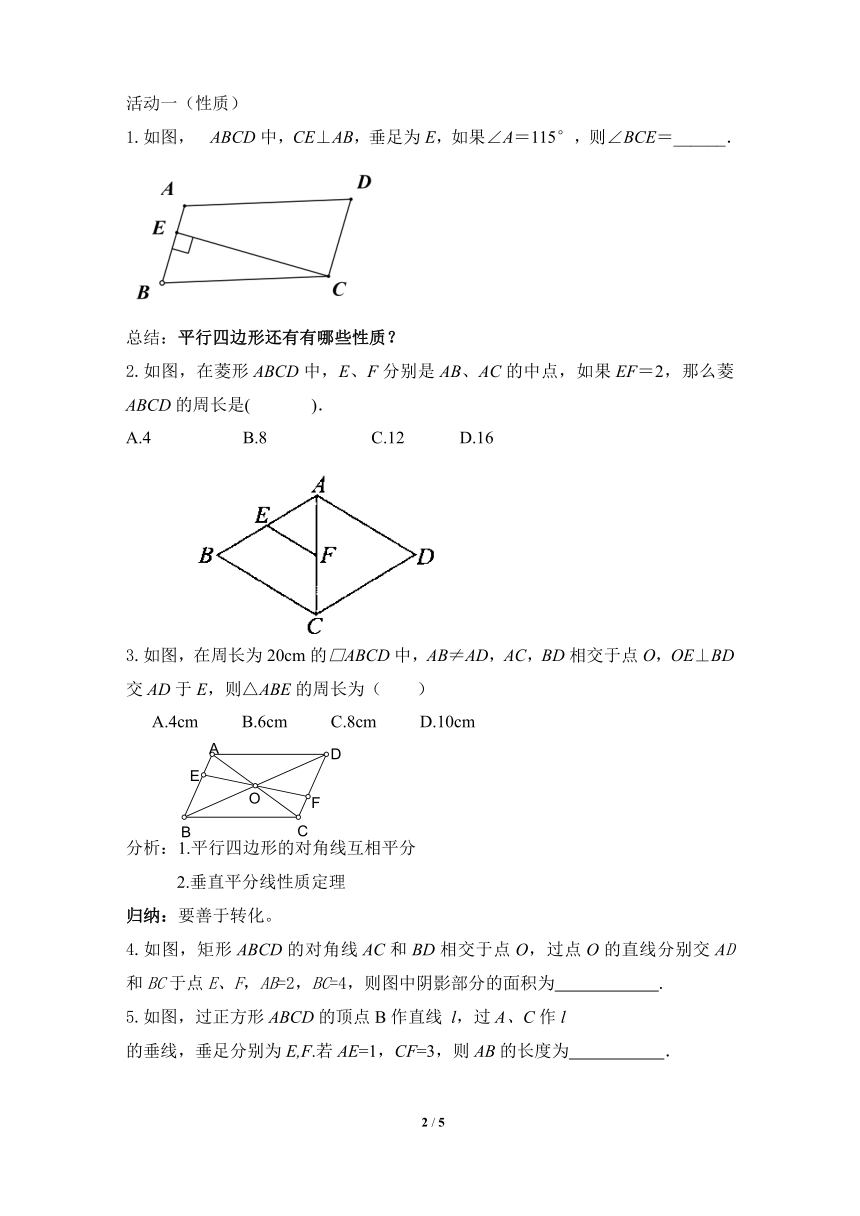
1.如图, ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE=______.
总结:平行四边形还有有哪些性质?
2.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=2,那么菱ABCD的周长是( ).
A.4 B.8 C.12 D.16
3.如图,在周长为20cm的□ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
A.4cm B.6cm C.8cm D.10cm
分析:1.平行四边形的对角线互相平分
2.垂直平分线性质定理
归纳:要善于转化。
4.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=4,则图中阴影部分的面积为 .
5.如图,过正方形ABCD的顶点B作直线 l,过A、C作l
的垂线,垂足分别为E,F.若AE=1,CF=3,则AB的长度为 .
方法总结:利用全等三角形进行转化
6.如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2.求①∠ABC的度数;②对角线AC、BD的长;③菱形ABCD的面积.
归纳: 菱形面积=底×高=对角线乘积的一半
拓展:所有对角线垂直的四边形都可以用此方法求面积
活动二(判定应用)
已知:如图,E、F为□ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种证法)
解题思路
方法一:
通过证明△ABE≌△CDF ,得到BE=DF.
方法二:
通过证明四边形BFDE是平行四边形, 得到BE=DF.
归纳总结:证明线段相等的方法有哪些?
活动三(综合应用)
四边形ABCD和四边形CEFH都是正方形,连接AF,M是AF中点,连接DM和EM.探究线段DM与EM的位置关系,并求的值.小聪同学的思路是:延长DM交EF于点N,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(1)如图,当点B、C、H在一条直线上时,线段DM与EM的位置关系是 , = ;
(2)如图,当点B、C、F在一条直线上时,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.
分析:第⑴题延长DM与EF交与N,先证明△ADM≌△FNM ,得出DM=MN, AD=NF,最后根据等腰三角形的“三线合一”的性质得出DM与EM 的关系。
由学生先总结第⑴题的方法,然后讨论完成第⑵题。
三、课堂练习
1. 如图,四边形ABCD是正方形,AE⊥BE于点E,且AE=3,BE=4,则阴影部分的面积是_________________.
2. 如图,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.求证:DE=BF.
3. 如图,矩形ABCD 的对角线AC、BD 相交于点O,CE⊥BO 于E,且DE:EB=3:1,OF⊥AB于F,OF=3,求矩形对角线的长.
4.如图,在菱形 ABCD和菱形BEFG 中,点A、B、E 在同一条直线上, P是线段DF的中点,连结PG、PC ,求证:PG⊥PC .
四、课堂小结,领悟思想方法
1.一题多变,举一反三。
经常在解题之后进行反思——改变命题的条件,或将命题的结论延伸,或将条件和结论互换,往往会有意想不到的收获。也只有这样,才能做到举一反三,提高应变能力。
2.一题多解,触类旁通。
在平时的作业或练习中,通过一题多解,你不仅可以从中对比选出最优方法,提高自己在应考中的解题效率,而且还能开阔你的思维,达到触类旁通的目的。
3.善于总结,领悟方法。
数学题目本身蕴含着许多数学思想方法,只要你善于总结,就能真正掌握、提炼出其中的数学方法,才能不断提高自己分析问题、解决问题的能力。
l
F
E
D
A
B
C
D
O
E
F
一个角
是直角
一组邻边相等
一组邻
边相等
一个角是直角
正方形
菱形
矩形
平行四边形
分别平行
两组对边
四边形
C
B
E
F
B
C
D
O
A
4 / 5
【教学目标】
1、通过对几种平行四边形的回顾与思考,使学生梳理所学的知识,系统地复习平行四边形与各种特殊平行四边形的定义、性质、判定方法,三角形的中位线定理等;
2、正确理解平行四边形与各种特殊平行四边形的联系与区别,在反思和交流过程中,逐渐建立知识体系;
3、引导学生独立思考,通过归纳、概括、实践等系统数学活动,感受获得成功的体验,形成科学的学习习惯。
【教学重点】
1、平行四边形与各种特殊平行四边形的区别。
2、梳理平行四边形、矩形、菱形、正方形、三角形的中位线定理的知识体系及应用方法。
【教学难点】
平行四边形与各种特殊平行四边形的定义、性质、判定的综合运用。
【教学模式】
以题代纲,梳理知识-----变式训练,查漏补缺-----综合训练,总结规律-----测试练习,提高效率。
【教具准备】实物投影仪、电脑、自制课件。
【教学过程】
一、梳理知识 开门见山,直奔主题
同学们,今天我们一起来复行四边形》的相关知识,先请同学们展示小组准备的知识结构图,请看大屏幕。
二、知识点复习
活动一(性质)
1.如图, ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE=______.
总结:平行四边形还有有哪些性质?
2.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=2,那么菱ABCD的周长是( ).
A.4 B.8 C.12 D.16
3.如图,在周长为20cm的□ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
A.4cm B.6cm C.8cm D.10cm
分析:1.平行四边形的对角线互相平分
2.垂直平分线性质定理
归纳:要善于转化。
4.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=4,则图中阴影部分的面积为 .
5.如图,过正方形ABCD的顶点B作直线 l,过A、C作l
的垂线,垂足分别为E,F.若AE=1,CF=3,则AB的长度为 .
方法总结:利用全等三角形进行转化
6.如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2.求①∠ABC的度数;②对角线AC、BD的长;③菱形ABCD的面积.
归纳: 菱形面积=底×高=对角线乘积的一半
拓展:所有对角线垂直的四边形都可以用此方法求面积
活动二(判定应用)
已知:如图,E、F为□ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种证法)
解题思路
方法一:
通过证明△ABE≌△CDF ,得到BE=DF.
方法二:
通过证明四边形BFDE是平行四边形, 得到BE=DF.
归纳总结:证明线段相等的方法有哪些?
活动三(综合应用)
四边形ABCD和四边形CEFH都是正方形,连接AF,M是AF中点,连接DM和EM.探究线段DM与EM的位置关系,并求的值.小聪同学的思路是:延长DM交EF于点N,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(1)如图,当点B、C、H在一条直线上时,线段DM与EM的位置关系是 , = ;
(2)如图,当点B、C、F在一条直线上时,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.
分析:第⑴题延长DM与EF交与N,先证明△ADM≌△FNM ,得出DM=MN, AD=NF,最后根据等腰三角形的“三线合一”的性质得出DM与EM 的关系。
由学生先总结第⑴题的方法,然后讨论完成第⑵题。
三、课堂练习
1. 如图,四边形ABCD是正方形,AE⊥BE于点E,且AE=3,BE=4,则阴影部分的面积是_________________.
2. 如图,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.求证:DE=BF.
3. 如图,矩形ABCD 的对角线AC、BD 相交于点O,CE⊥BO 于E,且DE:EB=3:1,OF⊥AB于F,OF=3,求矩形对角线的长.
4.如图,在菱形 ABCD和菱形BEFG 中,点A、B、E 在同一条直线上, P是线段DF的中点,连结PG、PC ,求证:PG⊥PC .
四、课堂小结,领悟思想方法
1.一题多变,举一反三。
经常在解题之后进行反思——改变命题的条件,或将命题的结论延伸,或将条件和结论互换,往往会有意想不到的收获。也只有这样,才能做到举一反三,提高应变能力。
2.一题多解,触类旁通。
在平时的作业或练习中,通过一题多解,你不仅可以从中对比选出最优方法,提高自己在应考中的解题效率,而且还能开阔你的思维,达到触类旁通的目的。
3.善于总结,领悟方法。
数学题目本身蕴含着许多数学思想方法,只要你善于总结,就能真正掌握、提炼出其中的数学方法,才能不断提高自己分析问题、解决问题的能力。
l
F
E
D
A
B
C
D
O
E
F
一个角
是直角
一组邻边相等
一组邻
边相等
一个角是直角
正方形
菱形
矩形
平行四边形
分别平行
两组对边
四边形
C
B
E
F
B
C
D
O
A
4 / 5
