华师大版八下数学 18.1.1平行四边形边、角的性质 教案
文档属性
| 名称 | 华师大版八下数学 18.1.1平行四边形边、角的性质 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 150.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-06 06:56:02 | ||
图片预览



文档简介
平行四边形及其性质教案
1、知识结构
2、教学重点和难点
重点:平行四边形的概念和性质。
难点:平行四边形性质定理的灵活应用。
平行四边形及其性质 第一课时
一、素质教育目标
1、知识教学点:使学生掌握平行四边形的概念,理解两条平行线间的距离的概念。掌握平行四边形的性质定理1、2。并能运用这些知识进行有关的证明或计算。
2、能力训练点:知道解决平行四边形问题的基本思想是化为三角形问题来处理,渗透转化思想。通过推导平行四边形的性质定理的过程,培养学生的推导、论证能力和逻辑思维能力。
3、德育渗透点:通过要求学生书写规范,培养学生科学严谨的学风。
4、美育渗透点:通过学习,渗透几何方法美和几何语言美及图形内在美和结构美。
二、学法引导:阅读、思考、讲解、分析、转化。
三、重点、难点、疑点及解决办法
1、教学重点:平行四边形性质定理的应用
2、教学难点:正确理解两条平行线间的距离的概念和运用性质定理2的推论;在计算或证明中综合应用本节前一章的知识。
3、疑点及解决办法:关于性质定理2的推论;两点的距离,点到直线的距离,两平行直线中间的距离的区别与联系,注重对概念的教学,使学生深刻理解上述概念,搞清它们之间的关系;平行四边形的高有关问题。
四、课时安排:2课时
五、教具学具准备:教具(做两个全等的三角形),投影仪,投影胶片,常用画图工具。
六、师生互动活动设计
教师复习提问,学习思考口答;教师设疑引思,学生讨论分析;师生共同总结结论,教师示范讲解,学生达标练习
第一课时
七、教学步骤
【复习提问】
1、什么叫做四边形?什么叫四边形的一组对边?
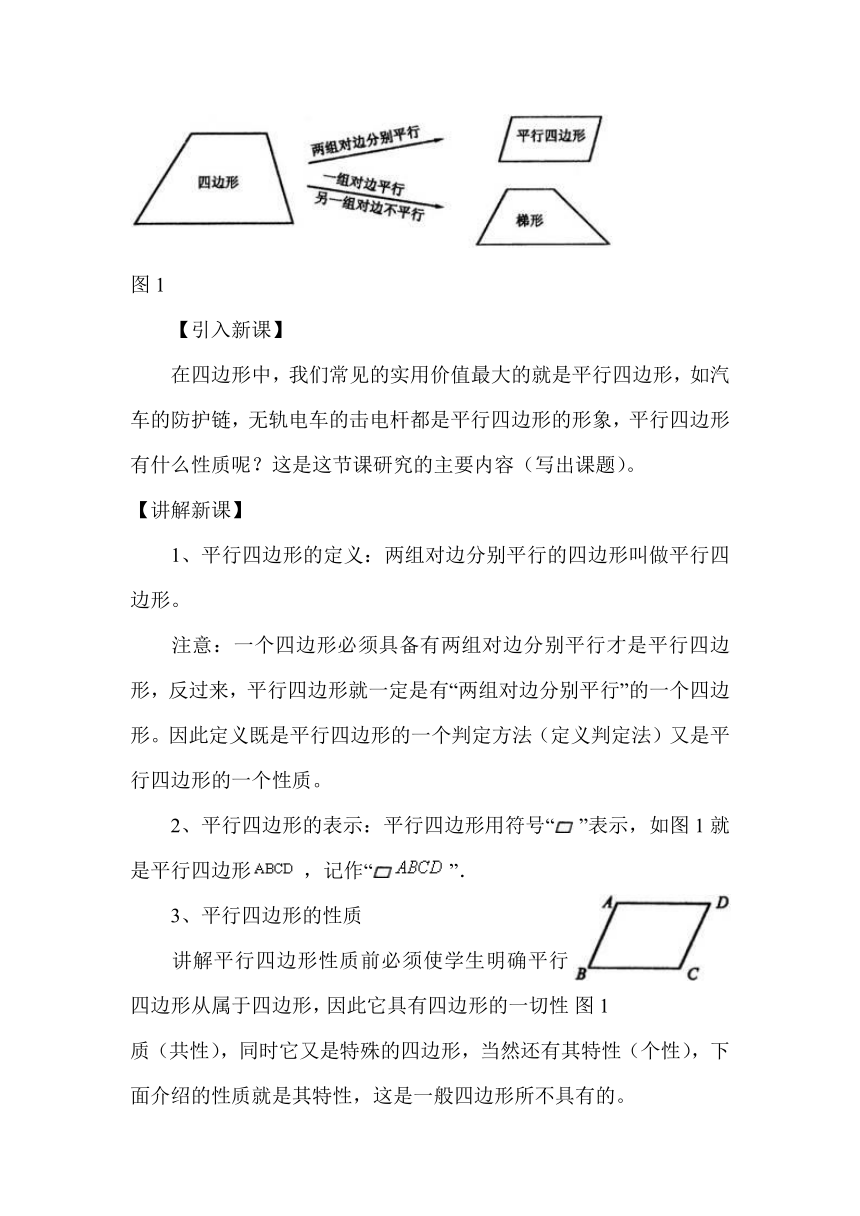
2、四边形的两组对边在位置上有几种可能?
(教师随着学生回答画出图1)
图1
【引入新课】
在四边形中,我们常见的实用价值最大的就是平行四边形,如汽车的防护链,无轨电车的击电杆都是平行四边形的形象,平行四边形有什么性质呢?这是这节课研究的主要内容(写出课题)。
【讲解新课】
1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形。
注意:一个四边形必须具备有两组对边分别平行才是平行四边形,反过来,平行四边形就一定是有“两组对边分别平行”的一个四边形。因此定义既是平行四边形的一个判定方法(定义判定法)又是平行四边形的一个性质。
2、平行四边形的表示:平行四边形用符号“ ”表示,如图1就是平行四边形 ,记作“ ”.
图1
3、平行四边形的性质
讲解平行四边形性质前必须使学生明确平行四边形从属于四边形,因此它具有四边形的一切性质(共性),同时它又是特殊的四边形,当然还有其特性(个性),下面介绍的性质就是其特性,这是一般四边形所不具有的。
平行四边形性质定理1:平行四边形的对角相等。
平行四边形性质定理2:平行四边形对边相等。
(教具用两个全等的三角形拼凑的平行四边形演示,由此得到证明以上两个定理的方法。如图2)
图2
如图3, , .
所以四边形 是平行四边形,所以 .
由此得到
推论:夹在两条平行线间的平行线段相等.
图3
要注意:必须有两个平行,即夹两条平行线段的两条直线平行,被夹的两条线段平行,缺一不可,如图4中的几种情况都不可以推出 .
图4
4.平行线间的距离
从推论可以知道,如果两条直线平行,那么从一条直线上所有各点到另一条直线的距离相等,如图5.
我们把两条平行线中一条直线上任意一点到另一条直线的距离,叫做平行线的距离.
图5
注意:(1)两相交直线无距离可言。
(2)连结两点间的线段的长度叫两点间的距离,从直线外一点到一条直线的垂线段的长,叫点到直线的距离.两条平行线中一条直线上任意一点到另一条直线的距离,叫做这两条平行线的距离,一定要注意这些概念之间的区别与联系。
例1 已知:如图1, , .
求证:(1) ; ; .
(2)△ 的顶点分别是△ 各边的中点(证法略),课堂提问(投影打出).
图1
①平行四边形两邻边的比为2:5,周长为28cm,则四条边长分别为___________.
②在 中,若 ,则 , .
【总结、扩展】
1、小结
本堂所讲的主要内容有
(1)平行四边形的概念,要理解这个概念的实质。
(2)平行四边形的部分性质。
①关于边的:对边平行;对边相等。
②关于角的:对角相等;邻角互补。
(3)“两平行线的距离”是一定值,不随垂线段的位置改变,即两平行线间的距离处处相等。
2.思考:如图.已知: 平面 , , 求证: .
八、布置作业
教材 ( http: / / www.teachercn.com / Kcgg / Jcyj / " \t "_blank )P141.2 (1)、(2)、(3) P142中 3(1)
九、板书设计
十、随堂练习
教材P.133中1、2、3
补充1.在 中 (1)若 ,则 度, 度, 度;(2)若 ,则 度, 度;(3)若 ,则 度, 度.
2. 中,周长为 ,△ 的周长比△ 周长多 则 , .
3. 中, 的平分线分 为长是 和 的两线段则 的周长是___________cm.
1、知识结构
2、教学重点和难点
重点:平行四边形的概念和性质。
难点:平行四边形性质定理的灵活应用。
平行四边形及其性质 第一课时
一、素质教育目标
1、知识教学点:使学生掌握平行四边形的概念,理解两条平行线间的距离的概念。掌握平行四边形的性质定理1、2。并能运用这些知识进行有关的证明或计算。
2、能力训练点:知道解决平行四边形问题的基本思想是化为三角形问题来处理,渗透转化思想。通过推导平行四边形的性质定理的过程,培养学生的推导、论证能力和逻辑思维能力。
3、德育渗透点:通过要求学生书写规范,培养学生科学严谨的学风。
4、美育渗透点:通过学习,渗透几何方法美和几何语言美及图形内在美和结构美。
二、学法引导:阅读、思考、讲解、分析、转化。
三、重点、难点、疑点及解决办法
1、教学重点:平行四边形性质定理的应用
2、教学难点:正确理解两条平行线间的距离的概念和运用性质定理2的推论;在计算或证明中综合应用本节前一章的知识。
3、疑点及解决办法:关于性质定理2的推论;两点的距离,点到直线的距离,两平行直线中间的距离的区别与联系,注重对概念的教学,使学生深刻理解上述概念,搞清它们之间的关系;平行四边形的高有关问题。
四、课时安排:2课时
五、教具学具准备:教具(做两个全等的三角形),投影仪,投影胶片,常用画图工具。
六、师生互动活动设计
教师复习提问,学习思考口答;教师设疑引思,学生讨论分析;师生共同总结结论,教师示范讲解,学生达标练习
第一课时
七、教学步骤
【复习提问】
1、什么叫做四边形?什么叫四边形的一组对边?
2、四边形的两组对边在位置上有几种可能?
(教师随着学生回答画出图1)
图1
【引入新课】
在四边形中,我们常见的实用价值最大的就是平行四边形,如汽车的防护链,无轨电车的击电杆都是平行四边形的形象,平行四边形有什么性质呢?这是这节课研究的主要内容(写出课题)。
【讲解新课】
1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形。
注意:一个四边形必须具备有两组对边分别平行才是平行四边形,反过来,平行四边形就一定是有“两组对边分别平行”的一个四边形。因此定义既是平行四边形的一个判定方法(定义判定法)又是平行四边形的一个性质。
2、平行四边形的表示:平行四边形用符号“ ”表示,如图1就是平行四边形 ,记作“ ”.
图1
3、平行四边形的性质
讲解平行四边形性质前必须使学生明确平行四边形从属于四边形,因此它具有四边形的一切性质(共性),同时它又是特殊的四边形,当然还有其特性(个性),下面介绍的性质就是其特性,这是一般四边形所不具有的。
平行四边形性质定理1:平行四边形的对角相等。
平行四边形性质定理2:平行四边形对边相等。
(教具用两个全等的三角形拼凑的平行四边形演示,由此得到证明以上两个定理的方法。如图2)
图2
如图3, , .
所以四边形 是平行四边形,所以 .
由此得到
推论:夹在两条平行线间的平行线段相等.
图3
要注意:必须有两个平行,即夹两条平行线段的两条直线平行,被夹的两条线段平行,缺一不可,如图4中的几种情况都不可以推出 .
图4
4.平行线间的距离
从推论可以知道,如果两条直线平行,那么从一条直线上所有各点到另一条直线的距离相等,如图5.
我们把两条平行线中一条直线上任意一点到另一条直线的距离,叫做平行线的距离.
图5
注意:(1)两相交直线无距离可言。
(2)连结两点间的线段的长度叫两点间的距离,从直线外一点到一条直线的垂线段的长,叫点到直线的距离.两条平行线中一条直线上任意一点到另一条直线的距离,叫做这两条平行线的距离,一定要注意这些概念之间的区别与联系。
例1 已知:如图1, , .
求证:(1) ; ; .
(2)△ 的顶点分别是△ 各边的中点(证法略),课堂提问(投影打出).
图1
①平行四边形两邻边的比为2:5,周长为28cm,则四条边长分别为___________.
②在 中,若 ,则 , .
【总结、扩展】
1、小结
本堂所讲的主要内容有
(1)平行四边形的概念,要理解这个概念的实质。
(2)平行四边形的部分性质。
①关于边的:对边平行;对边相等。
②关于角的:对角相等;邻角互补。
(3)“两平行线的距离”是一定值,不随垂线段的位置改变,即两平行线间的距离处处相等。
2.思考:如图.已知: 平面 , , 求证: .
八、布置作业
教材 ( http: / / www.teachercn.com / Kcgg / Jcyj / " \t "_blank )P141.2 (1)、(2)、(3) P142中 3(1)
九、板书设计
十、随堂练习
教材P.133中1、2、3
补充1.在 中 (1)若 ,则 度, 度, 度;(2)若 ,则 度, 度;(3)若 ,则 度, 度.
2. 中,周长为 ,△ 的周长比△ 周长多 则 , .
3. 中, 的平分线分 为长是 和 的两线段则 的周长是___________cm.
