华师大版数学八下 19.2.1菱形的性质 课件(16张PPT)
文档属性
| 名称 | 华师大版数学八下 19.2.1菱形的性质 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
19.2 菱 形
1 菱形的性质
华东师大·八年级数学下册
新课导入
回顾复行四边形有哪些特征 矩形与平行四边形比较有哪些特殊的特征
平行四边形
对边平行且相等
对角相等邻角互补
对角线互相平分
矩形
四个角是直角
对角线相等
接下来我们研讨下列问题
菱形的定义
菱形的特征
进行新课
做
一
做
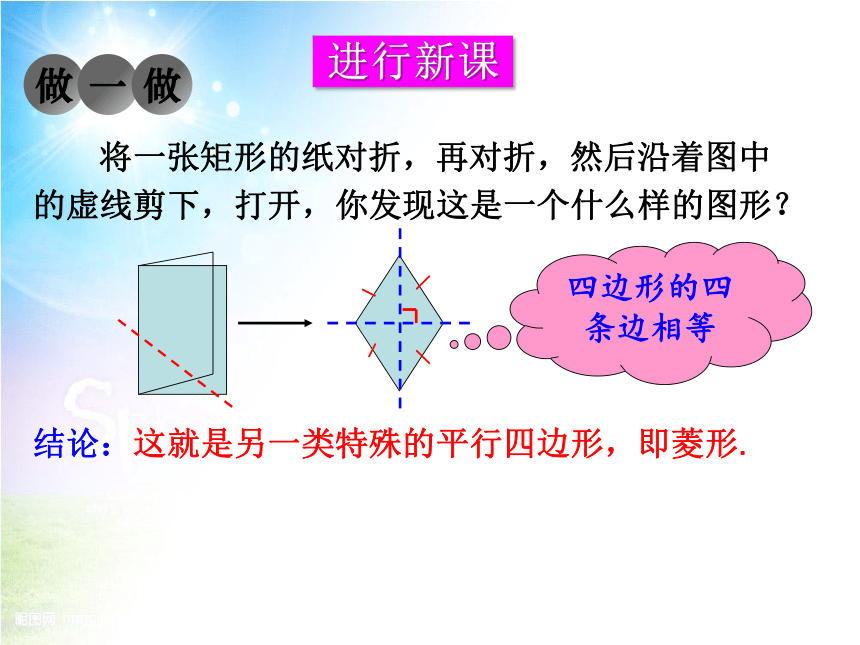
将一张矩形的纸对折,再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形?
四边形的四条边相等
结论:这就是另一类特殊的平行四边形,即菱形.
A
B
C
D
C
D
D
C
D
C
D
C
D
C
D
C
D
C
D
C
进行新课
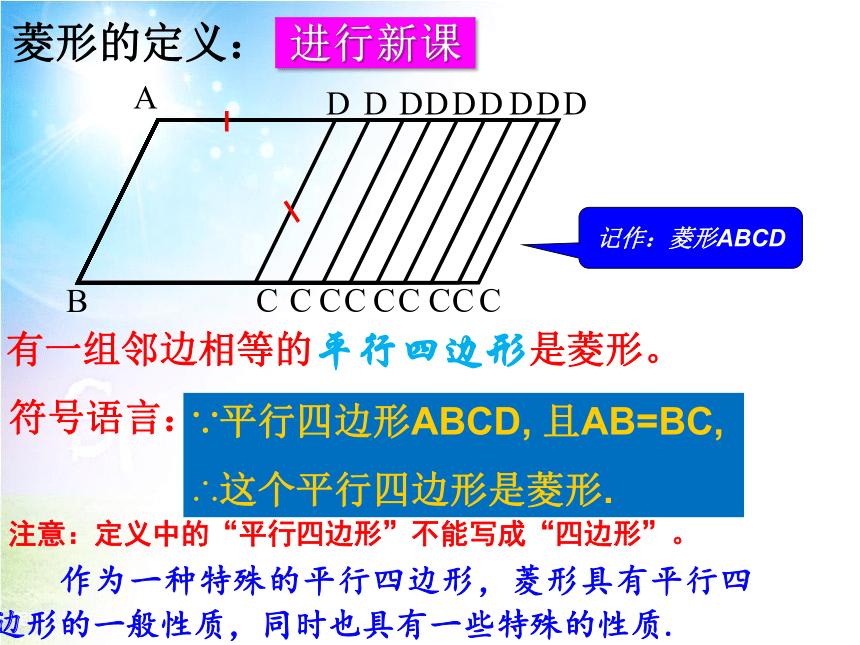
菱形的定义:
有一组邻边相等的平行四边形是菱形。
符号语言:
∵平行四边形ABCD, 且AB=BC,
∴这个平行四边形是菱形.
注意:定义中的“平行四边形”不能写成“四边形”。
作为一种特殊的平行四边形,菱形具有平行四边形的一般性质,同时也具有一些特殊的性质.
记作:菱形ABCD
自主学习,探究新知
中心对称;
对边平行且相等;
对角相等;
对角线互相平分;
对称性:
边:
角:
对角线:
菱形的性质
菱形的特殊性质
猜一猜
平行四边形的性质
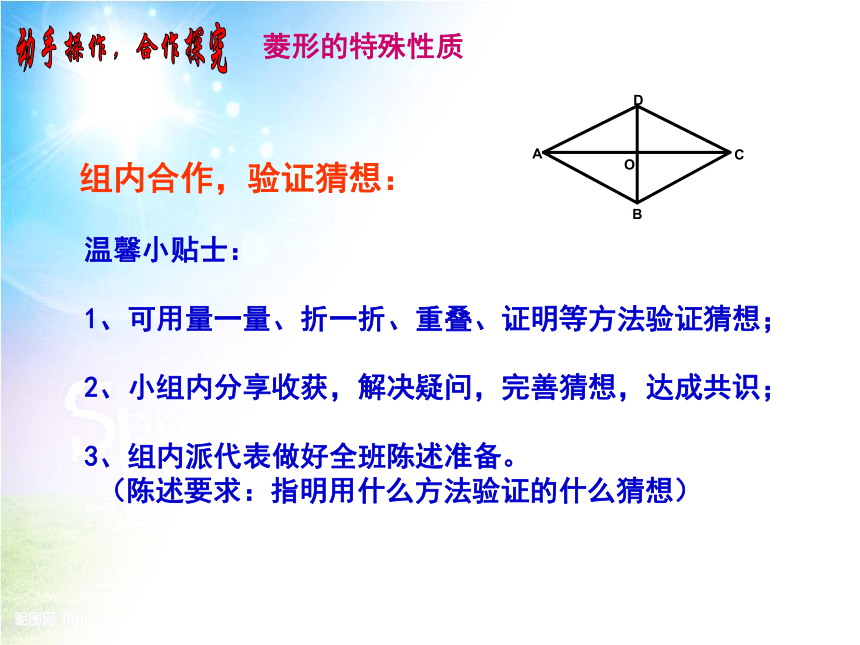
动手操作,合作探究
菱形的特殊性质
组内合作,验证猜想:
温馨小贴士:
1、可用量一量、折一折、重叠、证明等方法验证猜想;
2、小组内分享收获,解决疑问,完善猜想,达成共识;
3、组内派代表做好全班陈述准备。
(陈述要求:指明用什么方法验证的什么猜想)
自主学习,探究新知
中心对称;
对边平行且相等;
对角相等;
对角线互相平分;
平行四边形的性质
对称性:
边:
角:
对角线:
菱形的性质
菱形的特殊性质
轴对称
四边相等
对角线互相垂直,且每条对角线平分一组对角。
已知:如图,菱形ABCD
求证:AC⊥BD,BD平分∠ADC和∠ABC
证明:∵菱形ABCD
∴AD = CD,AB = BC,AO=OC
∴OD⊥AC,OD平分∠ADC,
菱形的对角线互相垂直,并且每一条对角线平分一组对角
A
B
C
D
O
即:AC⊥BD, BD平分∠ADC和∠ABC
OB平分∠ABC
菱形的特殊性质
合作学习,探究新知
∵菱形ABCD
∴ AC⊥BD,BD平分∠ADC和∠ABC
菱形的对角线互相垂直,并且每一条对角线平分一组对角
A
B
C
D
O
菱形的特殊性质
合作学习,探究新知
BD平分∠ADC和∠ABC
几何语言
1.一个菱形的周长为8cm,一条对角线长为2 cm.则这个菱形的
四个内角的度数为 。
2.菱形具有而平行四边形不一定具有的特征是( )
A、对角线互相平分 B、对边相等且平行
C、对角线平分一组对角 D、对角相等
60°、120°、60°、120°
C
巩固练习
3.在菱形ABCD中,∠BAD=2∠B,则∠B= ,
△ABC是 三角形,∠ABD的度数为________ 。
等边
30 °
60 °
A
B
C
D
如图,四边形ABCD是菱形,对角线AC、BD相交于点O,且 AB = 5,AO = 4,
则(1)菱形的周长为 ;
(2)BO = , AC = , BD = ;
(3) = ;
(4) = × = × = .
自主学习,发现新知
牛刀小试
24
4
6
6
8
3
20
2
合作学习,探索新知
通过“牛刀小试”的计算,你能发现菱形对角线的长与面积有什么关系吗?这个结论对所有菱形都成立吗?请简单说明理由。
先独立思考,
再组内交流合作
菱形
A
B
C
D
E
菱形的面积公式
例、如图,已知菱形ABCD的周长为24cm,对角线AC的长为8cm,求菱形的面积.
A
B
C
D
O
解:∵菱形的周长为24cm,
∴AB=6cm,又AC=8cm,∴OA=4cm,
因为AC⊥BD,∴OB= 2 (cm),
∴BD=4 ,
∴菱形ABCD的面积= AC·BD
= ×8×4
=16 (cm2)
典例讲解
菱形的定义:有一组邻边相等的平行四边形是菱形。
菱形的性质:
1.对边平行,且四边都相等;
3.对角线互相平分且互相垂直 .
2.对角相等;
菱形的面积: S菱形=底×高=
2
对角线的乘积
4.菱形既是中心对称图形,又是轴对称图形
课堂小结
1、如图,在菱形ABCD中,AC与BD相交于点O,AB=5,OA=4,求这一菱形的周长与两条对角线的长度。
解:
菱形的周长
AB+BC+CD+DA=4 AB = 4 × 5 = 20
对角线 AC=2AO=2×4=8,
BD=2BO=2×3=6
在△ABO中,根据勾股定理得
拓展提高
2、已知:如图,菱形ABCD中,E,F分别是CB,C
D上的点,且BE=DF. 求证:∠AEF=∠AFE.
证明:如图,连接AC,
∵四边形ABCD为菱形,
∴BC=CD,∠ECA=∠FCA.
又∵BE=DF,∴EC=FC.
∴△AEC≌△AFC,
∴AE=AF,∴∠AEF=∠AFE.
拓展提高
19.2 菱 形
1 菱形的性质
华东师大·八年级数学下册
新课导入
回顾复行四边形有哪些特征 矩形与平行四边形比较有哪些特殊的特征
平行四边形
对边平行且相等
对角相等邻角互补
对角线互相平分
矩形
四个角是直角
对角线相等
接下来我们研讨下列问题
菱形的定义
菱形的特征
进行新课
做
一
做
将一张矩形的纸对折,再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形?
四边形的四条边相等
结论:这就是另一类特殊的平行四边形,即菱形.
A
B
C
D
C
D
D
C
D
C
D
C
D
C
D
C
D
C
D
C
进行新课
菱形的定义:
有一组邻边相等的平行四边形是菱形。
符号语言:
∵平行四边形ABCD, 且AB=BC,
∴这个平行四边形是菱形.
注意:定义中的“平行四边形”不能写成“四边形”。
作为一种特殊的平行四边形,菱形具有平行四边形的一般性质,同时也具有一些特殊的性质.
记作:菱形ABCD
自主学习,探究新知
中心对称;
对边平行且相等;
对角相等;
对角线互相平分;
对称性:
边:
角:
对角线:
菱形的性质
菱形的特殊性质
猜一猜
平行四边形的性质
动手操作,合作探究
菱形的特殊性质
组内合作,验证猜想:
温馨小贴士:
1、可用量一量、折一折、重叠、证明等方法验证猜想;
2、小组内分享收获,解决疑问,完善猜想,达成共识;
3、组内派代表做好全班陈述准备。
(陈述要求:指明用什么方法验证的什么猜想)
自主学习,探究新知
中心对称;
对边平行且相等;
对角相等;
对角线互相平分;
平行四边形的性质
对称性:
边:
角:
对角线:
菱形的性质
菱形的特殊性质
轴对称
四边相等
对角线互相垂直,且每条对角线平分一组对角。
已知:如图,菱形ABCD
求证:AC⊥BD,BD平分∠ADC和∠ABC
证明:∵菱形ABCD
∴AD = CD,AB = BC,AO=OC
∴OD⊥AC,OD平分∠ADC,
菱形的对角线互相垂直,并且每一条对角线平分一组对角
A
B
C
D
O
即:AC⊥BD, BD平分∠ADC和∠ABC
OB平分∠ABC
菱形的特殊性质
合作学习,探究新知
∵菱形ABCD
∴ AC⊥BD,BD平分∠ADC和∠ABC
菱形的对角线互相垂直,并且每一条对角线平分一组对角
A
B
C
D
O
菱形的特殊性质
合作学习,探究新知
BD平分∠ADC和∠ABC
几何语言
1.一个菱形的周长为8cm,一条对角线长为2 cm.则这个菱形的
四个内角的度数为 。
2.菱形具有而平行四边形不一定具有的特征是( )
A、对角线互相平分 B、对边相等且平行
C、对角线平分一组对角 D、对角相等
60°、120°、60°、120°
C
巩固练习
3.在菱形ABCD中,∠BAD=2∠B,则∠B= ,
△ABC是 三角形,∠ABD的度数为________ 。
等边
30 °
60 °
A
B
C
D
如图,四边形ABCD是菱形,对角线AC、BD相交于点O,且 AB = 5,AO = 4,
则(1)菱形的周长为 ;
(2)BO = , AC = , BD = ;
(3) = ;
(4) = × = × = .
自主学习,发现新知
牛刀小试
24
4
6
6
8
3
20
2
合作学习,探索新知
通过“牛刀小试”的计算,你能发现菱形对角线的长与面积有什么关系吗?这个结论对所有菱形都成立吗?请简单说明理由。
先独立思考,
再组内交流合作
菱形
A
B
C
D
E
菱形的面积公式
例、如图,已知菱形ABCD的周长为24cm,对角线AC的长为8cm,求菱形的面积.
A
B
C
D
O
解:∵菱形的周长为24cm,
∴AB=6cm,又AC=8cm,∴OA=4cm,
因为AC⊥BD,∴OB= 2 (cm),
∴BD=4 ,
∴菱形ABCD的面积= AC·BD
= ×8×4
=16 (cm2)
典例讲解
菱形的定义:有一组邻边相等的平行四边形是菱形。
菱形的性质:
1.对边平行,且四边都相等;
3.对角线互相平分且互相垂直 .
2.对角相等;
菱形的面积: S菱形=底×高=
2
对角线的乘积
4.菱形既是中心对称图形,又是轴对称图形
课堂小结
1、如图,在菱形ABCD中,AC与BD相交于点O,AB=5,OA=4,求这一菱形的周长与两条对角线的长度。
解:
菱形的周长
AB+BC+CD+DA=4 AB = 4 × 5 = 20
对角线 AC=2AO=2×4=8,
BD=2BO=2×3=6
在△ABO中,根据勾股定理得
拓展提高
2、已知:如图,菱形ABCD中,E,F分别是CB,C
D上的点,且BE=DF. 求证:∠AEF=∠AFE.
证明:如图,连接AC,
∵四边形ABCD为菱形,
∴BC=CD,∠ECA=∠FCA.
又∵BE=DF,∴EC=FC.
∴△AEC≌△AFC,
∴AE=AF,∴∠AEF=∠AFE.
拓展提高
