函数专题复习--数学思想在函数中的应用学案
文档属性
| 名称 | 函数专题复习--数学思想在函数中的应用学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 104.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-21 00:00:00 | ||
图片预览


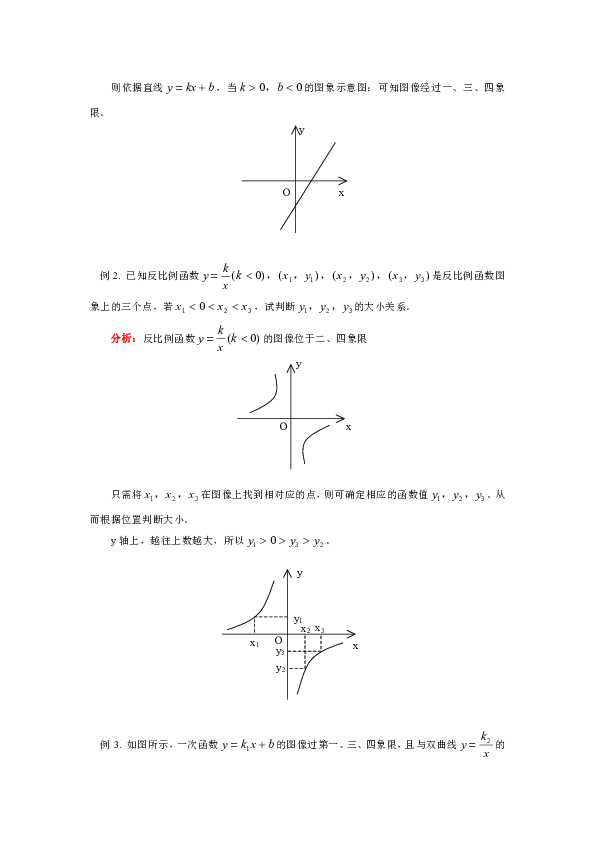
文档简介
暑假专题——函数解题中的数学思想应用
重点、难点
数学思想的应用
【典型例题】
一. 方程思想的应用
例1. 已知点P(x,x+y)与点Q(y+5,x-7)关于x轴对称,则点Q坐标为______。
分析:P点关于x轴对称时,横坐标不变,纵坐标相反
构造方程组
解得:
∴Q点坐标为(4,-3)
例2. 已知一次函数的图像经过第一、二、三象限,求m的值。
分析:一次函数条件:x的次数为1
即:
得:
解得:
而当
此时图像经过一、三、四象限
不符合题意,舍去
故m=3
例3. 已知:在△ABC中,,P为AB上一动点(P不与A、B重合),过点P作PE//BC交AC于E,连结BE,设AP=x,△BPE的面积为y,求y与x之间的函数关系,并求自变量x的取值范围。
分析:
∴知道PE的长、EC的长是关键,而PE、EC与三角形相似有关。
所以此题借助比例式找出PE、EC与x之间的等量关系。
即:用含x的式子表示PE、EC,进而得到函数关系式。
解:
二. 数形结合思想的应用
例1. 一次函数的图像经过第_______象限。
分析:充当中的k,此时大于0
充当中的b,此时小于0
则依据直线,当的图象示意图:可知图像经过一、三、四象限。
例2. 已知反比例函数是反比例函数图象上的三个点,若,试判断的大小关系。
分析:反比例函数的图像位于二、四象限
只需将在图像上找到相对应的点,则可确定相应的函数值。从而根据位置判断大小。
y轴上,越往上数越大,所以。
例3. 如图所示,一次函数的图像过第一、三、四象限,且与双曲线的图像交于A、B两点,与y轴交于C,是终边上的一点,若,原点O到A点的距离为
(1)求A点坐标;
(2)求反比例函数的解析式;
(3)若,求一次函数的解析式。
分析:此题关键是在平面直角坐标系中借助及,在Rt△中求A点坐标。从而进一步借助到y轴距离等于,求出b,确定一次函数的解析式。
解:(1)设点A坐标为(a,b),且
过A作轴交x轴于M
则
在
所以点A坐标为(5,1)
(2)此反比例函数解析式为
(3),且(OC=|b|,C在x轴下方)
∴一次函数解析式为:
又∵直线过点
∴一次函数解析式为
三. 分类讨论思想的应用
例1. 已知点N在x轴下方,且到x轴距离为2,到y轴距离为,则点N的坐标为_________。
分析:设点N坐标为(x,y)
由题意得:
则
又∵点N在x轴下方,y<0
例2. 已知直线与直角坐标系的两坐标轴围成的三角形的面积为9,则直线解析式为__________。
分析:设直线与x轴交点为A,与y轴交点为B
则
∴直线解析式为
例3. 已知点A为平面直角坐标系内第四象限夹角平分线上一点,且OA=5,试在坐标轴上找一点C,使得△AOC为等腰三角形,并写出C点坐标。
分析:首先应分别在x轴和y轴上找点C
其次,△AOC应分类找:(1)OA为腰;(2)OA为底
当C点在x轴上时
当C点在y轴上时
四. 转化思想的应用
例1. 已知一次函数的图像经过二、三、四象限,求k的取值范围。
分析:直线经过二、三、四象限
则
得:
所以
例2. 待定系数解题(转化为方程组)
如:已知与成正比例,其中m,n是常数,当时,;当时,,求y与x的函数关系。
分析:设
当时,得:
当时,得:
解方程组
解得:
所求函数关系式为:
例3. 如图所示,直线与y轴交于点A(0,3)与x轴交于点B,正方形OPQR的两边在坐标轴上,Q在直线AB上,OP:PB=1:2,求直线的解析式。
分析:求直线AB解析式,需要知道A、B坐标。而A点(0,3),则OA=3,求B点即可,即求OB长,此问题转化为几何问题。
又知PQRO为正方形,设正方形边长为x,则
∴B点坐标为(6,0)
∴直线解析式为
五. 几何解题思想的综合应用
例:已知反比例函数和一次函数,其中一次函数的图象经过(a,b),(a+1,b+k)两点。
(1)求反比例函数的解析式;
(2)如图所示,已知点A是上述两个函数的图象在第一象限的交点,求点A的坐标;
(3)利用(2)的结果,回答:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由。
分析:(1)由一次函数的图象经过两点(a,b),(a+1,b+k),代入消去a,b,可得k=2,进而可确定反比例函数的关系式。
(2)将联立成方程组,易求出点A的坐标;
(3)应根据OA为腰和底进行分类,结合(2)探求出点P的存在性。
解:(1)依题意可得:
两式相减,得
所以反比例函数的解析式为
(2)由,得,
经检验都是原方程组的解。
因为A点在第一象限,所以A点坐标为(1,1)
(3),OA与x轴所夹锐角为45°
如图下所示①,当OA为腰时,由OA=OP,得
由,得
②当OA为底时,得
所以这样的点有4个,分别是、
【模拟试题】(答题时间:30分钟)
1. 反比例函数的图象上两点,,当时,有,则m的取值范围是_____________。
2. 已知反比例函数的图象在第一、三象限,则一次函数的图象不经过第___________象限。
3. 直线与y轴的交点在x轴上方,且y随x的增大而减小,则m的取值范围是__________。
4. 三角形三边长为3cm,5cm,xcm,则三角形的周长为与的函数关系式是______________,自变量x的取值范围是___________。
5. 当m取何值时,函数是x的一次函数?它是否是正比例函数?
6. 已知一次函数的图象经过第一、三、四象限,求m的取值范围。
7. 直线和直线的交点在第__________象限。
8. 两个一次函数的图象交于y轴上一点A,分别交x轴于点B、C,如图所示,若已知|OB|:|OA|:|OC|=1:2:3,且△ABC的面积是16,求两函数的解析式。
9. 在平面直角坐标系中,已知点在第二象限,且m为整数,则过点A的反比例函数的解析式为________________。
10. 如果一次函数的图象与两坐标轴所围成的三角形的面积为10,则此一次函数为_________________。
11. 已知点A是正比例函数和反比例函数在第一象限的交点
(1)求点A的坐标;
(2)如果直线经过点A且与x轴交于点C,求b及点C的坐标。
12. 如图所示,在第四象限内的矩形OABC,两边在坐标轴上,一个顶点在一次函数的图象上,当点A从左向右移动时,矩形的周长与面积也随之发生变化,设线段OA长m,矩形的周长为,面积为s。
(1)试分别写出与m的函数关系;
(2)能否求出当m取何值时,矩形的周长最大?为什么?
(3)你能否估计矩形的面积是否有最大值,简单说一下你的想法?
【试题答案】
1. 2. 三
3. 4.
5. 解:,
则
,它是一次函数也是正比例函数。
6. 解:,
7. 三
8. 解:设
∴直线AB解析式为,直线AC解析式为
9.
10.
11. 解:(1),解得:(不合题意,舍去)
(2)经过点
则
12. 解:(1)①由题意得,
②
(2)周长的一次函数,且的增大而增大。是否有最大值,关键在于m的取值范围。与x轴交点为(6,0),所以,m越接近6,周长越大。但不能等于6,所以周长无最大值。
(3)当点A接近于(0,0)时,面积接近于0,随着点A逐渐右移,面积逐渐增大。而当点A接近于(6,0),面积也接近于0,随着点A位置变化,可知面积先随m的增大而增大,到一定程度时,开始随x的增大而减小,估计在m取某一值时,面积为最大值。
重点、难点
数学思想的应用
【典型例题】
一. 方程思想的应用
例1. 已知点P(x,x+y)与点Q(y+5,x-7)关于x轴对称,则点Q坐标为______。
分析:P点关于x轴对称时,横坐标不变,纵坐标相反
构造方程组
解得:
∴Q点坐标为(4,-3)
例2. 已知一次函数的图像经过第一、二、三象限,求m的值。
分析:一次函数条件:x的次数为1
即:
得:
解得:
而当
此时图像经过一、三、四象限
不符合题意,舍去
故m=3
例3. 已知:在△ABC中,,P为AB上一动点(P不与A、B重合),过点P作PE//BC交AC于E,连结BE,设AP=x,△BPE的面积为y,求y与x之间的函数关系,并求自变量x的取值范围。
分析:
∴知道PE的长、EC的长是关键,而PE、EC与三角形相似有关。
所以此题借助比例式找出PE、EC与x之间的等量关系。
即:用含x的式子表示PE、EC,进而得到函数关系式。
解:
二. 数形结合思想的应用
例1. 一次函数的图像经过第_______象限。
分析:充当中的k,此时大于0
充当中的b,此时小于0
则依据直线,当的图象示意图:可知图像经过一、三、四象限。
例2. 已知反比例函数是反比例函数图象上的三个点,若,试判断的大小关系。
分析:反比例函数的图像位于二、四象限
只需将在图像上找到相对应的点,则可确定相应的函数值。从而根据位置判断大小。
y轴上,越往上数越大,所以。
例3. 如图所示,一次函数的图像过第一、三、四象限,且与双曲线的图像交于A、B两点,与y轴交于C,是终边上的一点,若,原点O到A点的距离为
(1)求A点坐标;
(2)求反比例函数的解析式;
(3)若,求一次函数的解析式。
分析:此题关键是在平面直角坐标系中借助及,在Rt△中求A点坐标。从而进一步借助到y轴距离等于,求出b,确定一次函数的解析式。
解:(1)设点A坐标为(a,b),且
过A作轴交x轴于M
则
在
所以点A坐标为(5,1)
(2)此反比例函数解析式为
(3),且(OC=|b|,C在x轴下方)
∴一次函数解析式为:
又∵直线过点
∴一次函数解析式为
三. 分类讨论思想的应用
例1. 已知点N在x轴下方,且到x轴距离为2,到y轴距离为,则点N的坐标为_________。
分析:设点N坐标为(x,y)
由题意得:
则
又∵点N在x轴下方,y<0
例2. 已知直线与直角坐标系的两坐标轴围成的三角形的面积为9,则直线解析式为__________。
分析:设直线与x轴交点为A,与y轴交点为B
则
∴直线解析式为
例3. 已知点A为平面直角坐标系内第四象限夹角平分线上一点,且OA=5,试在坐标轴上找一点C,使得△AOC为等腰三角形,并写出C点坐标。
分析:首先应分别在x轴和y轴上找点C
其次,△AOC应分类找:(1)OA为腰;(2)OA为底
当C点在x轴上时
当C点在y轴上时
四. 转化思想的应用
例1. 已知一次函数的图像经过二、三、四象限,求k的取值范围。
分析:直线经过二、三、四象限
则
得:
所以
例2. 待定系数解题(转化为方程组)
如:已知与成正比例,其中m,n是常数,当时,;当时,,求y与x的函数关系。
分析:设
当时,得:
当时,得:
解方程组
解得:
所求函数关系式为:
例3. 如图所示,直线与y轴交于点A(0,3)与x轴交于点B,正方形OPQR的两边在坐标轴上,Q在直线AB上,OP:PB=1:2,求直线的解析式。
分析:求直线AB解析式,需要知道A、B坐标。而A点(0,3),则OA=3,求B点即可,即求OB长,此问题转化为几何问题。
又知PQRO为正方形,设正方形边长为x,则
∴B点坐标为(6,0)
∴直线解析式为
五. 几何解题思想的综合应用
例:已知反比例函数和一次函数,其中一次函数的图象经过(a,b),(a+1,b+k)两点。
(1)求反比例函数的解析式;
(2)如图所示,已知点A是上述两个函数的图象在第一象限的交点,求点A的坐标;
(3)利用(2)的结果,回答:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由。
分析:(1)由一次函数的图象经过两点(a,b),(a+1,b+k),代入消去a,b,可得k=2,进而可确定反比例函数的关系式。
(2)将联立成方程组,易求出点A的坐标;
(3)应根据OA为腰和底进行分类,结合(2)探求出点P的存在性。
解:(1)依题意可得:
两式相减,得
所以反比例函数的解析式为
(2)由,得,
经检验都是原方程组的解。
因为A点在第一象限,所以A点坐标为(1,1)
(3),OA与x轴所夹锐角为45°
如图下所示①,当OA为腰时,由OA=OP,得
由,得
②当OA为底时,得
所以这样的点有4个,分别是、
【模拟试题】(答题时间:30分钟)
1. 反比例函数的图象上两点,,当时,有,则m的取值范围是_____________。
2. 已知反比例函数的图象在第一、三象限,则一次函数的图象不经过第___________象限。
3. 直线与y轴的交点在x轴上方,且y随x的增大而减小,则m的取值范围是__________。
4. 三角形三边长为3cm,5cm,xcm,则三角形的周长为与的函数关系式是______________,自变量x的取值范围是___________。
5. 当m取何值时,函数是x的一次函数?它是否是正比例函数?
6. 已知一次函数的图象经过第一、三、四象限,求m的取值范围。
7. 直线和直线的交点在第__________象限。
8. 两个一次函数的图象交于y轴上一点A,分别交x轴于点B、C,如图所示,若已知|OB|:|OA|:|OC|=1:2:3,且△ABC的面积是16,求两函数的解析式。
9. 在平面直角坐标系中,已知点在第二象限,且m为整数,则过点A的反比例函数的解析式为________________。
10. 如果一次函数的图象与两坐标轴所围成的三角形的面积为10,则此一次函数为_________________。
11. 已知点A是正比例函数和反比例函数在第一象限的交点
(1)求点A的坐标;
(2)如果直线经过点A且与x轴交于点C,求b及点C的坐标。
12. 如图所示,在第四象限内的矩形OABC,两边在坐标轴上,一个顶点在一次函数的图象上,当点A从左向右移动时,矩形的周长与面积也随之发生变化,设线段OA长m,矩形的周长为,面积为s。
(1)试分别写出与m的函数关系;
(2)能否求出当m取何值时,矩形的周长最大?为什么?
(3)你能否估计矩形的面积是否有最大值,简单说一下你的想法?
【试题答案】
1. 2. 三
3. 4.
5. 解:,
则
,它是一次函数也是正比例函数。
6. 解:,
7. 三
8. 解:设
∴直线AB解析式为,直线AC解析式为
9.
10.
11. 解:(1),解得:(不合题意,舍去)
(2)经过点
则
12. 解:(1)①由题意得,
②
(2)周长的一次函数,且的增大而增大。是否有最大值,关键在于m的取值范围。与x轴交点为(6,0),所以,m越接近6,周长越大。但不能等于6,所以周长无最大值。
(3)当点A接近于(0,0)时,面积接近于0,随着点A逐渐右移,面积逐渐增大。而当点A接近于(6,0),面积也接近于0,随着点A位置变化,可知面积先随m的增大而增大,到一定程度时,开始随x的增大而减小,估计在m取某一值时,面积为最大值。
