人教A版(2019)必修第二册8.6空间直线、平面的垂直(Word含答案解析)
文档属性
| 名称 | 人教A版(2019)必修第二册8.6空间直线、平面的垂直(Word含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 19:11:00 | ||
图片预览




文档简介
人教A版(2019)必修第二册 8.6 空间直线、平面的垂直
一、单选题
1.已知平面内的,射线与所成的角均为135°,则与平面所成的角的余弦值是( )
A. B. C. D.
2.已知几何体是正方体,则( )
A.平面 B.在直线上存在一点E,使得
C.平面 D.在直线上存在一点E,使得平面
3.如图,矩形中,已知为的中点.将沿着向上翻折至得到四棱锥.平面与平面所成锐二面角为,直线与平面所成角为,则下列说法错误的是( )
A.若为中点,则无论翻折到哪个位置都有平面平面
B.若为中点,则无论翻折到哪个位置都有平面
C.
D.存在某一翻折位置,使
4.已知直线和平面,下列说法错误的是( )
A.若,,则 B.若,,,则
C.若,,,则 D.若,,则.
5.如图,在正方形中,E、F分别为、的中点,H是的中点.现沿、、把这个正方形折成一个几何体,使B、C、D三点重合于点G,则下列结论中成立的是( )
A.平面 B.平面
C.平面 D.平面
6.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
A. B.- C.2 D.
7.如图,在正方体中,点P为线段上的动点(点与,不重合),则下列说法不正确的是( )
A.
B.三棱锥的体积为定值
C.过,,三点作正方体的截面,截面图形为三角形或梯形
D.DP与平面所成角的正弦值最大为
8.如图,在三棱锥中,,,、、分别是所在棱的中点.则下列说法错误的是( )
A.面面 B.面面 C. D.
9.埃及胡夫金字塔是世界七大奇迹之一,它的形状可视为一个正四棱锥,现已测得它的塔倾角为,则该四棱锥的高与底面正方形的边长的比值为( )(注:塔倾角是指该四棱锥的侧面与底面所成的二面角,参考数据:)
A. B. C. D.
10.直线与平面内的无数条直线垂直,则直线与平面的关系是( )
A.和平面平行 B.和平面垂直 C.在平面内 D.不能确定
11.已知直线平面,直线,则( )
A. B.
C.异面 D.相交而不垂直
12.比萨斜塔是意大利的著名景点,因斜而不倒的奇特景象而世界闻名.把地球看成一个球(球心记为),地球上一点的纬度是指与地球赤道所在平面所成角,的方向即为点处的竖直方向.已知比萨斜塔处于北纬,经过测量,比萨斜塔朝正南方向倾斜,且其中轴线与竖直方向的夹角为,则中轴线与赤道所在平面所成的角为( )
A. B. C. D.
二、填空题
13.如图,正方体的棱长为1,,分别是棱,的中点,过直线的平面分别与棱,交于点,,设,给出下列四个结论:
①四边形一定为菱形;
②若四边形的面积为,,则有最大值;
③若四棱锥的体积为,,则为单调函数;
④设与交于点,连接,在线段上取点,在线段上取点,则的最小值为.
其中所有正确结论的序号是________.
14.已知是空间两个不同的平面,是空间两条不同的直线,给出的下列说法:
①若,且,则;
②若,且,则;
③若,且,则;
④若,且,则.
其中正确的说法为__________(填序号)
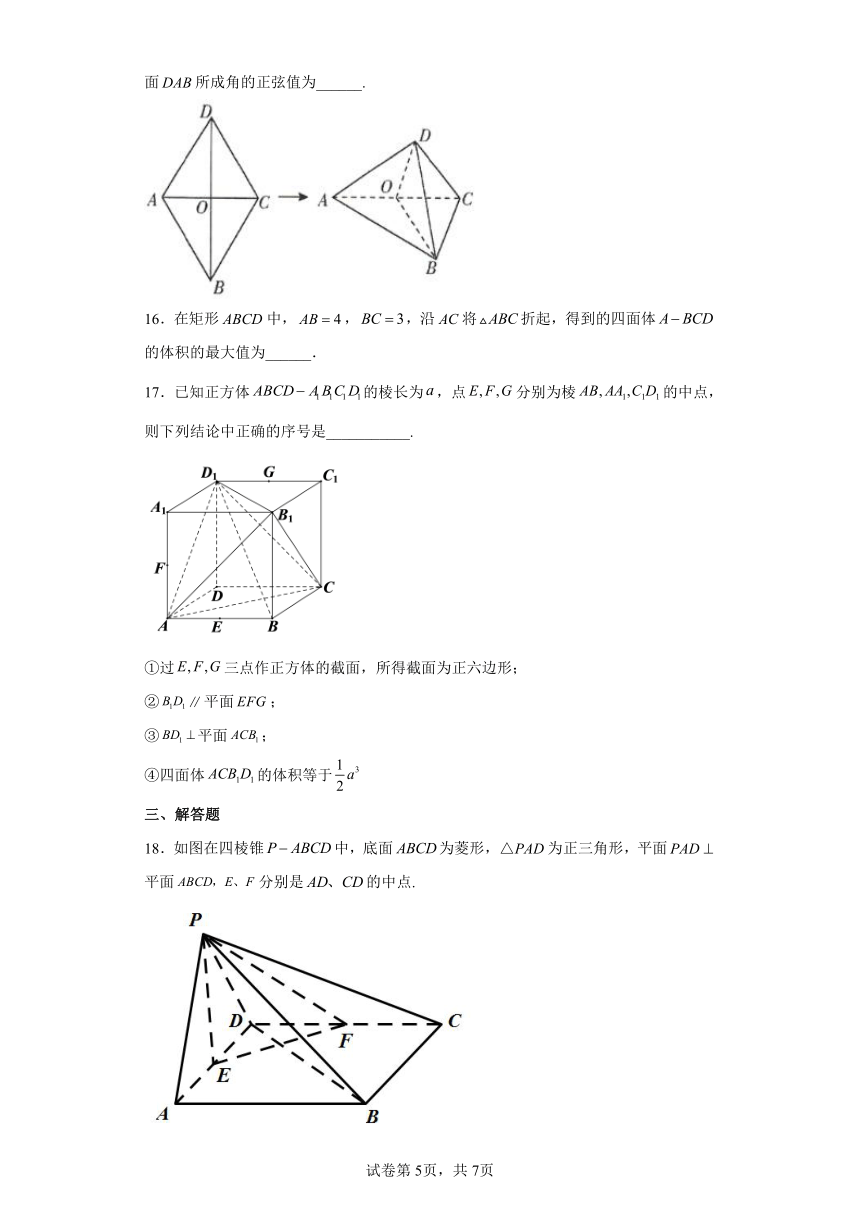
15.如图,已知边长为4的菱形中,.将菱形沿对角线折起得到三棱锥,二面角的大小为60°,则直线与平面所成角的正弦值为______.
16.在矩形ABCD中,,,沿AC将折起,得到的四面体的体积的最大值为______.
17.已知正方体的棱长为,点分别为棱的中点,则下列结论中正确的序号是___________.
①过三点作正方体的截面,所得截面为正六边形;
②平面;
③平面;
④四面体的体积等于
三、解答题
18.如图在四棱锥中,底面为菱形,为正三角形,平面平面分别是的中点.
(1)证明:;
(2)若M是棱上一点,三棱锥与三棱锥的体积相等,求M点的位置.
19.如图所示,是等边三角形,,,面面,.
(1)求证:;
(2)求四面体的体积.
20.在正三棱台中,是边长为的等边三角形,且.已知,,,分别是线段,的中点,当直线上一动点在射线上时,,.
(1)证明:平面;
(2)求直线与平面所成角的正弦值;
(3)连接,,已知点在平面投影是,平面是一个分别以,作为,轴的复平面,.当时,请直接写出的虚部(不要求写出过程).
21.已知多面体ABCDEF如图所示,其中四边形ABCD为菱形,AF平面CDE,且A,D,E,F四点共面.
(1)求证∶平面ABF平面CDE;
(2)若∠ABC=90°,且AD=5,DE=6,AF=2,,求证∶AD⊥CE.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
作出图形,如图,通过分析,可得为与平面所成的角的补角,利用余弦定理可以计算.
【详解】
作出如下图形,令,则,,
取中点,连接,则即为与平面所成的角的补角,
在中,,
在中,,
,
,
与平面所成的角的余弦值是.
故选:B.
本题考查线面角的求法,找出所成角,构造三角形是解题的关键.
2.D
与平面相交,所以选项A错误;假设在直线上存在一点E,使得,找到矛盾,所以选项B错误;假设平面,找到矛盾,所以选项C错误;当E与重合时, 平面,所以选项D正确.
【详解】
由题得与平面相交,所以选项A错误;
假设在直线上存在一点E,使得,因为,所以,这不可能,所以选项B错误;
假设平面,则平面,所以平面,所以, 实际上,,所以平面不可能,所以选项C错误;
当E与重合时,因为平面,平面,所以平面,所以选项D正确.
故选:D
3.C
对于A:根据线面垂直的判定和面面垂直的判定可判断;
对于B:取中点,根据三角形的中位线的性质可证得四边形PECQ是平行四边形,再由线面平行的判定可判断;
对于C:过作平面,则在上,所以平面与平面所成锐二面角为或其补角,根据面面角和线面角的定义可判断;
对于D:根据面面角和线面角的定义可判断.
【详解】
若为中点,连接交于点,则面,又面,所以平面平面,故A正确;
取中点,则,,又,
所以四边形PECQ是平行四边形,又平面,平面,所以平面,故B正确;
过作平面,则在上,所以平面与平面所成锐二面角为(或其补角),
,故C错误;
若,又,则,故D正确,
故选:C.
方法点睛:空间直线、平面平行或垂直等位置关系命题的真假判断,除了利用定理、公理、推理判断外,还常采用画图(尤其是画长方体)、现实实物判断法(如墙角、桌面等)、排除筛选法等;另外,若原命题不太容易判断真假,可以考虑它的逆否命题,判断它的逆否命题真假,原命题与逆否命题等价.
4.D
根据空间中线面平行或垂直的判定定理和性质定理对各选项逐一分析即可求解.
【详解】
解:对A:若,,则由面面平行的性质有,所以A正确;
对B:若,,则由线面平行的性质有,又,
从而由面面垂直的判定定理有,所以B正确;
对C:若,,则,又,所以,所以C正确;
对D:若,,则或,所以D错误.
故选:D.
5.A
根据题意,结合线面垂直的判定与性质,一一判断即可.
【详解】
对于选项A,∵B、C、D重合于点G,∴,,,
∴平面,故A正确;
对于选项B,由A选项可知,平面,因与不平行,知不垂直与平面,故B错;
对于选项C,由不与垂直,得不与垂直,进而可知不垂直于平面,
故C错;
对于选项D,由B选项可知,不垂直于平面,且,得不垂直,进而可知不垂直于平面.
故选:A.
6.A
如图所示,分别取,,,的中点,,,,则,,,或其补角 为异面直线与所成角.
【详解】
解:如图所示,
分别取,,,的中点,,,,则,,,
或其补角为异面直线与所成角.
设,则,,
,
异面直线与所成角的余弦值为,
故选:A.
平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:
①平移:平移异面直线中的一条或两条,作出异面直线所成的角;
②认定:证明作出的角就是所求异面直线所成的角;
③计算:求该角的值,常利用解三角形;
④取舍:由异面直线所成的角的取值范围是,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.
7.D
A.通过平面进行说明;B.根据等体积法进行说明;C.分析点位置,作出截面图形后进行判断;D.先分析线面为,然后表示出,通过分析的长度确定出正弦值的最大值.
【详解】
由题可知平面,所以,故A正确;
由等体积法得为定值,故B正确;
设的中点为,当时,如下图所示:
此时截面是三角形,
当时,如下图所示:
此时截面是梯形,故C正确;
选项D,在正方体中,连接,则为在平面上的射影,则为与平面所成的角,
设正方体的棱长为1,,则,,
当取得最小值时,的值最大,即时,的值最小为,
所以的值最大为,故D不正确.
故选:D.
方法点睛:作空间几何体截面的常见方法:
(1)直接连接法:有两点在几何体的同一个面上,连接该两点即为几何体与截面的交线,找截面就是找交线的过程;
(2)作平行线法:过直线与直线外一点作截面,若直线所在的平面与点所在的平面平行,可以通过过点找直线的平行线找到几何体与截面的交线;
(3) 作延长线找交点法:若直线相交但是立体图形中未体现,可通过作延长线的方法先找到交点,然后借助交点找到截面形成的交线;
(4)辅助平面法:若三个点两两都不在一个侧面或者底面中,则在作截面时需要作一个辅助平面.
8.D
根据中位线定理和面面平行的判定定理判断,根据平面判断,,反证法判断.
【详解】
解:、分别是,的中点,
,又平面,平面,
平面,
同理可得平面,
又,平面平面,故正确;
,,,
平面,
,故正确,
又平面,
平面平面,故正确;
假设,又,
,与矛盾,故与不平行,故错误,
故选:D
关键点睛:解题关键在于利用中位线定理和面面平行的判定定理求解,属于基础题
9.B
作出图形,设O为正方形ABCD的中心,E为CD的中点,先证明是侧面与底面所成的角,再设,,,由求解.
【详解】
如图所示:
O为正方形ABCD的中心,E为CD的中点,
则,
所以平面PEO,
所以,
所以是侧面与底面所成的角,
则,
设,,,
由题意得:,
解得.
故选:B.
10.D
根据题意,画出图形判断.
【详解】
如图所示:
由图形知和平面平行,和平面垂直或在平面内,
故选:D
11.A
根据线面垂直的定义得解.
【详解】
由线面垂直的定义,若直线与平面垂直,则直线垂直与该平面内的任意一条直线,
因此
故选:A
本题考查线面垂直的定义,属于基础题.
12.A
由题意画出示意图,即可选出正确答案.
【详解】
解析如图所示,为比萨斜塔的中轴线,,,则,中轴线与赤道所在平面所成的角为.
故选:A.
13.①④
①根据面面平行的性质可证明四边形的两组对边分别平行,再证明对角线互相垂直即可证明其是菱形;
②四边形面积,EF为定值,MN最大时为最大,观察MN变化即可判断最值情况;
③连结、、,则四棱锥被分割成两个小的三棱锥,它们是都以为底,以、分别为顶点的两个三棱锥.底面△的面积是一个定值.高也为定值,故可判断体积为定值.
④将Rt沿着翻转到与矩形在同一平面,过作于Q,交于,则此时最短.
【详解】
①平面∥平面,平面平面=EN,平面平面=MF,
.同理可证.
四边形为平行四边形.
连接MN、AC、BD、:
∵四边形ABCD是正方形,∴AC⊥BD,
∵⊥平面ABCD,∴⊥AC,
∵BD=B,∴AC⊥平面,
∵MN平面,∴AC⊥MN.
∵EA与FC平行且相等,
∴ACFE是平行四边形,
∴AC∥EF,
∴EF垂直MN,
∴MEFN是菱形.故①正确.
②四边形面积,EF为定值,当为B或时,即x=0或x=1时,最长,此时面积最大,但0<x<1,即M不能取线段的端点,∴四边形MENF面积无最大值.故②错误.
③连结、、,则四棱锥被分割成两个小的三棱锥,它们是都以为底,以、分别为顶点的两个三棱锥.
△的面积是一个定值.
同②中证明AC⊥平面,也可证明BD⊥平面,
则B到平面AEF的距离即为.
∵B∥A,∴B∥平面AEF,
∴M到平面AEF的距离即为B到平面AEF的距离,
同理N到平面AEF的距离也为,
∴、到平面的距离之和是定值BD,
∴四棱锥的体积为常数.故③错误.
④如图,将Rt沿着翻转到与矩形在同一平面,过作于Q,交于,则此时最短.
过作于,
则四边形是直角梯形,
由题可知是中点,是梯形的中位线,∴
设,设
在中,,,
,
∴在中,
∴.故④正确.
故答案为:①④.
本题综合考察空间点线面的位置关系,④中的关键是把空间问题平面化,将空间里面的两边之和最短转化为平面内三点共线时长度最短问题求解.
14.③④
利用空间线面、面面平行、垂直的性质定理和判定定理分别分析四个命题,得到正确答案.
【详解】
①,,且,则可能相交,故①错误;
②,,且,则可能相交,也可能平行,故②错误;
③,,且,则,根据线面垂直的性质可知③正确;
④,、且,则,根据线面垂直的性质可知④正确.
故答案为:③④.
15.
由,可算得点C到平面的距离为d,又由直线BC与平面所成角的正弦值为,即可得到本题答案.
【详解】
∵四边形是菱形,,
,
为二面角的平面角,
,
是等边三角形.
取的中点,连接,则.
,
平面,
又平面,平面,
平面,
,
,
的边上的高,
,
设点到平面的距离为,则.
,,
∴直线与平面所成角的正弦值为.
本题主要考查立体几何与折叠图形的综合问题,其中涉及到直线与平面所成角的求解.
16.##4.8
由题意当平面平面时,四面体的体积最大值,过作交于点,则为高,从而可得答案.
【详解】
由,,则
沿AC将折起,当平面平面时,四面体的体积最大值.
过作交于点,由平面平面,且平面平面
所以平面,则为此时四面体的高. 且
所以
故答案为:
17.①③
根据平面的性质作出截面即可判断①,根据与相交可判断②,证明和可判断③,求出四面体的体积可判断④.
【详解】
延长,分别交的延长线交于,连接交于,设与的延长线交于,连接交于,交于,连接,则截面六边形为正六边形,故①正确;
与相交,故与平面相交,故②错误;
因为正方体中,平面,所以,因为,,所以平面,所以,同理可得,因为,所以平面,故③正确;
四面体的体积等于正方体的体积减去四个正三棱锥的体积,即为,故④错误.
故答案为:①③.
18.(1)证明见解析;(2)M点在上靠近P点的四等分点处.
(1)连接,由,可证明,,从而得平面,得证线线垂直;
(2)设设,则,根据棱锥的体积公式,利用体积法得出结论,由,,可得值.
【详解】
(1)连接且E是的中点,.
又平面平面,平面平面平面.
平面平面.
又为菱形,且分别为棱的中点,.
,又平面;
平面.
(2)如图,连接,
设,则,
,
,则,又.
.
解得,即M点在上靠近P点的四等分点处.
方法点睛:本题考查由线面垂直证明线线垂直,考查由体积法求线段的比值.若是棱锥棱上一点,则.三棱锥求体积时可以换底,这样求体积比较灵活简便.
19.(1)证明见解析;(2)1.
(1)由余弦定理可得,根据勾股定理的逆定理得,结合即可得出结果.
(2)由面面垂直的性质定理得平面,且,根据线线平行得出平面平面,进而得到与到底面的距离相等,结合棱锥体积公式即可.
【详解】
(1)证明:,,
又是等边三角形,
,
又,
在中,由余弦定理可得,
,
,故,
又,;
(2)解:取的中点,连接,
由,得,
又平面平面,
且平面平面,
平面,
且求得.
由,平面平面,
可得平面,
则与到底面的距离相等,
则四面体的体积.
(1)证明线线垂直的方法主要有:线面垂直的性质定理、勾股定理的逆定理或者采用空间向量法;
(2) 求三棱锥的体积时要注意三棱锥的每个面都可以作为底面,例如三棱锥的三条侧棱两两垂直,我们就选择其中的一个侧面作为底面,另一条侧棱作为高来求体积.
20.(1)证明见解析
(2)
(3)
(1)过点作面,过点作,证明面,可得面,进而可得,求出、、的长,由勾股定理逆定理可证明,再由线面垂直的判定定理即可求证;
(2)过点作面,由对称性可得点在直线上,即为与平面所成角,在中,由正弦定理求得,延长、交于点,可得为的中位线,在中,由余弦定理可得的值,进而可得的值,再计算即可求解;
(3)根据已知条件分析在上的投影,即可得的虚部.
(1)
过点作面,过点作,
因为边长为的等边三角形,且上底面与下底面相似,比边长之为,
所以,
在正三棱台中,连接,因为面,
则点必落在上,,
因为为等边三角形,是线段的中点,可得,
因为面,面,,所以面,
因为,所以面,所以,,
因为,所以是的中点,
因为,所以,
因为是的中点,所以,
所以,可得,
因为,,所以平面,
(2)
过点作面,由对称性可得点在直线上,
因为,
在中,由正弦定理可得:,
即,所以,所以,
因为为梯形的一条高,
所以即为与平面所成角,
因为,,,,
延长、交于点,
因为,,所以为的中位线,
所以,,
在中,由余弦定理可得:,
所以,
所以,
所以直线与平面所成角的正弦值为.
(3)
.
21.(1)证明见解析;(2)证明见解析.
(1)根据四边形ABCD是菱形可得 AB平面CDE,再结合AF平面CDE即可证明;
(2)根据已知条件结合线面平行性质得AFDE,再在线段ED上取一点G,使得EG=4,进而根据几何关系得AD⊥ED,AD⊥DC,即可通过AD⊥平面CDE证得结论.
【详解】
证明:(1)∵ 四边形ABCD是菱形,∴ABCD,
∵AB平面CDE,CD平面CDE,∴AB平面CDE,
又AF平面CDE,AF∩AB=A,∴平面ABF平面CDE.
(2)AF平面CDE,AF平面ADEF,平面ADEF∩平面CDE=DE,
∴AFDE.
在线段ED上取一点G,使得EG=4,则DG=2=AF,
又∵DGAF,∴四边形ADGF是平行四边形,
∴FG=AD=5,FGAD,
∵,∴,
∴EG⊥FG,∴AD⊥ ED.
∵∠ABC=90°,四边形ABCD是菱形,
∴AD⊥DC,
又DC∩DE=D,∴AD⊥平面CDE,
∵CE平面CDE,∴AD⊥CE.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知平面内的,射线与所成的角均为135°,则与平面所成的角的余弦值是( )
A. B. C. D.
2.已知几何体是正方体,则( )
A.平面 B.在直线上存在一点E,使得
C.平面 D.在直线上存在一点E,使得平面
3.如图,矩形中,已知为的中点.将沿着向上翻折至得到四棱锥.平面与平面所成锐二面角为,直线与平面所成角为,则下列说法错误的是( )
A.若为中点,则无论翻折到哪个位置都有平面平面
B.若为中点,则无论翻折到哪个位置都有平面
C.
D.存在某一翻折位置,使
4.已知直线和平面,下列说法错误的是( )
A.若,,则 B.若,,,则
C.若,,,则 D.若,,则.
5.如图,在正方形中,E、F分别为、的中点,H是的中点.现沿、、把这个正方形折成一个几何体,使B、C、D三点重合于点G,则下列结论中成立的是( )
A.平面 B.平面
C.平面 D.平面
6.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
A. B.- C.2 D.
7.如图,在正方体中,点P为线段上的动点(点与,不重合),则下列说法不正确的是( )
A.
B.三棱锥的体积为定值
C.过,,三点作正方体的截面,截面图形为三角形或梯形
D.DP与平面所成角的正弦值最大为
8.如图,在三棱锥中,,,、、分别是所在棱的中点.则下列说法错误的是( )
A.面面 B.面面 C. D.
9.埃及胡夫金字塔是世界七大奇迹之一,它的形状可视为一个正四棱锥,现已测得它的塔倾角为,则该四棱锥的高与底面正方形的边长的比值为( )(注:塔倾角是指该四棱锥的侧面与底面所成的二面角,参考数据:)
A. B. C. D.
10.直线与平面内的无数条直线垂直,则直线与平面的关系是( )
A.和平面平行 B.和平面垂直 C.在平面内 D.不能确定
11.已知直线平面,直线,则( )
A. B.
C.异面 D.相交而不垂直
12.比萨斜塔是意大利的著名景点,因斜而不倒的奇特景象而世界闻名.把地球看成一个球(球心记为),地球上一点的纬度是指与地球赤道所在平面所成角,的方向即为点处的竖直方向.已知比萨斜塔处于北纬,经过测量,比萨斜塔朝正南方向倾斜,且其中轴线与竖直方向的夹角为,则中轴线与赤道所在平面所成的角为( )
A. B. C. D.
二、填空题
13.如图,正方体的棱长为1,,分别是棱,的中点,过直线的平面分别与棱,交于点,,设,给出下列四个结论:
①四边形一定为菱形;
②若四边形的面积为,,则有最大值;
③若四棱锥的体积为,,则为单调函数;
④设与交于点,连接,在线段上取点,在线段上取点,则的最小值为.
其中所有正确结论的序号是________.
14.已知是空间两个不同的平面,是空间两条不同的直线,给出的下列说法:
①若,且,则;
②若,且,则;
③若,且,则;
④若,且,则.
其中正确的说法为__________(填序号)
15.如图,已知边长为4的菱形中,.将菱形沿对角线折起得到三棱锥,二面角的大小为60°,则直线与平面所成角的正弦值为______.
16.在矩形ABCD中,,,沿AC将折起,得到的四面体的体积的最大值为______.
17.已知正方体的棱长为,点分别为棱的中点,则下列结论中正确的序号是___________.
①过三点作正方体的截面,所得截面为正六边形;
②平面;
③平面;
④四面体的体积等于
三、解答题
18.如图在四棱锥中,底面为菱形,为正三角形,平面平面分别是的中点.
(1)证明:;
(2)若M是棱上一点,三棱锥与三棱锥的体积相等,求M点的位置.
19.如图所示,是等边三角形,,,面面,.
(1)求证:;
(2)求四面体的体积.
20.在正三棱台中,是边长为的等边三角形,且.已知,,,分别是线段,的中点,当直线上一动点在射线上时,,.
(1)证明:平面;
(2)求直线与平面所成角的正弦值;
(3)连接,,已知点在平面投影是,平面是一个分别以,作为,轴的复平面,.当时,请直接写出的虚部(不要求写出过程).
21.已知多面体ABCDEF如图所示,其中四边形ABCD为菱形,AF平面CDE,且A,D,E,F四点共面.
(1)求证∶平面ABF平面CDE;
(2)若∠ABC=90°,且AD=5,DE=6,AF=2,,求证∶AD⊥CE.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
作出图形,如图,通过分析,可得为与平面所成的角的补角,利用余弦定理可以计算.
【详解】
作出如下图形,令,则,,
取中点,连接,则即为与平面所成的角的补角,
在中,,
在中,,
,
,
与平面所成的角的余弦值是.
故选:B.
本题考查线面角的求法,找出所成角,构造三角形是解题的关键.
2.D
与平面相交,所以选项A错误;假设在直线上存在一点E,使得,找到矛盾,所以选项B错误;假设平面,找到矛盾,所以选项C错误;当E与重合时, 平面,所以选项D正确.
【详解】
由题得与平面相交,所以选项A错误;
假设在直线上存在一点E,使得,因为,所以,这不可能,所以选项B错误;
假设平面,则平面,所以平面,所以, 实际上,,所以平面不可能,所以选项C错误;
当E与重合时,因为平面,平面,所以平面,所以选项D正确.
故选:D
3.C
对于A:根据线面垂直的判定和面面垂直的判定可判断;
对于B:取中点,根据三角形的中位线的性质可证得四边形PECQ是平行四边形,再由线面平行的判定可判断;
对于C:过作平面,则在上,所以平面与平面所成锐二面角为或其补角,根据面面角和线面角的定义可判断;
对于D:根据面面角和线面角的定义可判断.
【详解】
若为中点,连接交于点,则面,又面,所以平面平面,故A正确;
取中点,则,,又,
所以四边形PECQ是平行四边形,又平面,平面,所以平面,故B正确;
过作平面,则在上,所以平面与平面所成锐二面角为(或其补角),
,故C错误;
若,又,则,故D正确,
故选:C.
方法点睛:空间直线、平面平行或垂直等位置关系命题的真假判断,除了利用定理、公理、推理判断外,还常采用画图(尤其是画长方体)、现实实物判断法(如墙角、桌面等)、排除筛选法等;另外,若原命题不太容易判断真假,可以考虑它的逆否命题,判断它的逆否命题真假,原命题与逆否命题等价.
4.D
根据空间中线面平行或垂直的判定定理和性质定理对各选项逐一分析即可求解.
【详解】
解:对A:若,,则由面面平行的性质有,所以A正确;
对B:若,,则由线面平行的性质有,又,
从而由面面垂直的判定定理有,所以B正确;
对C:若,,则,又,所以,所以C正确;
对D:若,,则或,所以D错误.
故选:D.
5.A
根据题意,结合线面垂直的判定与性质,一一判断即可.
【详解】
对于选项A,∵B、C、D重合于点G,∴,,,
∴平面,故A正确;
对于选项B,由A选项可知,平面,因与不平行,知不垂直与平面,故B错;
对于选项C,由不与垂直,得不与垂直,进而可知不垂直于平面,
故C错;
对于选项D,由B选项可知,不垂直于平面,且,得不垂直,进而可知不垂直于平面.
故选:A.
6.A
如图所示,分别取,,,的中点,,,,则,,,或其补角 为异面直线与所成角.
【详解】
解:如图所示,
分别取,,,的中点,,,,则,,,
或其补角为异面直线与所成角.
设,则,,
,
异面直线与所成角的余弦值为,
故选:A.
平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:
①平移:平移异面直线中的一条或两条,作出异面直线所成的角;
②认定:证明作出的角就是所求异面直线所成的角;
③计算:求该角的值,常利用解三角形;
④取舍:由异面直线所成的角的取值范围是,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.
7.D
A.通过平面进行说明;B.根据等体积法进行说明;C.分析点位置,作出截面图形后进行判断;D.先分析线面为,然后表示出,通过分析的长度确定出正弦值的最大值.
【详解】
由题可知平面,所以,故A正确;
由等体积法得为定值,故B正确;
设的中点为,当时,如下图所示:
此时截面是三角形,
当时,如下图所示:
此时截面是梯形,故C正确;
选项D,在正方体中,连接,则为在平面上的射影,则为与平面所成的角,
设正方体的棱长为1,,则,,
当取得最小值时,的值最大,即时,的值最小为,
所以的值最大为,故D不正确.
故选:D.
方法点睛:作空间几何体截面的常见方法:
(1)直接连接法:有两点在几何体的同一个面上,连接该两点即为几何体与截面的交线,找截面就是找交线的过程;
(2)作平行线法:过直线与直线外一点作截面,若直线所在的平面与点所在的平面平行,可以通过过点找直线的平行线找到几何体与截面的交线;
(3) 作延长线找交点法:若直线相交但是立体图形中未体现,可通过作延长线的方法先找到交点,然后借助交点找到截面形成的交线;
(4)辅助平面法:若三个点两两都不在一个侧面或者底面中,则在作截面时需要作一个辅助平面.
8.D
根据中位线定理和面面平行的判定定理判断,根据平面判断,,反证法判断.
【详解】
解:、分别是,的中点,
,又平面,平面,
平面,
同理可得平面,
又,平面平面,故正确;
,,,
平面,
,故正确,
又平面,
平面平面,故正确;
假设,又,
,与矛盾,故与不平行,故错误,
故选:D
关键点睛:解题关键在于利用中位线定理和面面平行的判定定理求解,属于基础题
9.B
作出图形,设O为正方形ABCD的中心,E为CD的中点,先证明是侧面与底面所成的角,再设,,,由求解.
【详解】
如图所示:
O为正方形ABCD的中心,E为CD的中点,
则,
所以平面PEO,
所以,
所以是侧面与底面所成的角,
则,
设,,,
由题意得:,
解得.
故选:B.
10.D
根据题意,画出图形判断.
【详解】
如图所示:
由图形知和平面平行,和平面垂直或在平面内,
故选:D
11.A
根据线面垂直的定义得解.
【详解】
由线面垂直的定义,若直线与平面垂直,则直线垂直与该平面内的任意一条直线,
因此
故选:A
本题考查线面垂直的定义,属于基础题.
12.A
由题意画出示意图,即可选出正确答案.
【详解】
解析如图所示,为比萨斜塔的中轴线,,,则,中轴线与赤道所在平面所成的角为.
故选:A.
13.①④
①根据面面平行的性质可证明四边形的两组对边分别平行,再证明对角线互相垂直即可证明其是菱形;
②四边形面积,EF为定值,MN最大时为最大,观察MN变化即可判断最值情况;
③连结、、,则四棱锥被分割成两个小的三棱锥,它们是都以为底,以、分别为顶点的两个三棱锥.底面△的面积是一个定值.高也为定值,故可判断体积为定值.
④将Rt沿着翻转到与矩形在同一平面,过作于Q,交于,则此时最短.
【详解】
①平面∥平面,平面平面=EN,平面平面=MF,
.同理可证.
四边形为平行四边形.
连接MN、AC、BD、:
∵四边形ABCD是正方形,∴AC⊥BD,
∵⊥平面ABCD,∴⊥AC,
∵BD=B,∴AC⊥平面,
∵MN平面,∴AC⊥MN.
∵EA与FC平行且相等,
∴ACFE是平行四边形,
∴AC∥EF,
∴EF垂直MN,
∴MEFN是菱形.故①正确.
②四边形面积,EF为定值,当为B或时,即x=0或x=1时,最长,此时面积最大,但0<x<1,即M不能取线段的端点,∴四边形MENF面积无最大值.故②错误.
③连结、、,则四棱锥被分割成两个小的三棱锥,它们是都以为底,以、分别为顶点的两个三棱锥.
△的面积是一个定值.
同②中证明AC⊥平面,也可证明BD⊥平面,
则B到平面AEF的距离即为.
∵B∥A,∴B∥平面AEF,
∴M到平面AEF的距离即为B到平面AEF的距离,
同理N到平面AEF的距离也为,
∴、到平面的距离之和是定值BD,
∴四棱锥的体积为常数.故③错误.
④如图,将Rt沿着翻转到与矩形在同一平面,过作于Q,交于,则此时最短.
过作于,
则四边形是直角梯形,
由题可知是中点,是梯形的中位线,∴
设,设
在中,,,
,
∴在中,
∴.故④正确.
故答案为:①④.
本题综合考察空间点线面的位置关系,④中的关键是把空间问题平面化,将空间里面的两边之和最短转化为平面内三点共线时长度最短问题求解.
14.③④
利用空间线面、面面平行、垂直的性质定理和判定定理分别分析四个命题,得到正确答案.
【详解】
①,,且,则可能相交,故①错误;
②,,且,则可能相交,也可能平行,故②错误;
③,,且,则,根据线面垂直的性质可知③正确;
④,、且,则,根据线面垂直的性质可知④正确.
故答案为:③④.
15.
由,可算得点C到平面的距离为d,又由直线BC与平面所成角的正弦值为,即可得到本题答案.
【详解】
∵四边形是菱形,,
,
为二面角的平面角,
,
是等边三角形.
取的中点,连接,则.
,
平面,
又平面,平面,
平面,
,
,
的边上的高,
,
设点到平面的距离为,则.
,,
∴直线与平面所成角的正弦值为.
本题主要考查立体几何与折叠图形的综合问题,其中涉及到直线与平面所成角的求解.
16.##4.8
由题意当平面平面时,四面体的体积最大值,过作交于点,则为高,从而可得答案.
【详解】
由,,则
沿AC将折起,当平面平面时,四面体的体积最大值.
过作交于点,由平面平面,且平面平面
所以平面,则为此时四面体的高. 且
所以
故答案为:
17.①③
根据平面的性质作出截面即可判断①,根据与相交可判断②,证明和可判断③,求出四面体的体积可判断④.
【详解】
延长,分别交的延长线交于,连接交于,设与的延长线交于,连接交于,交于,连接,则截面六边形为正六边形,故①正确;
与相交,故与平面相交,故②错误;
因为正方体中,平面,所以,因为,,所以平面,所以,同理可得,因为,所以平面,故③正确;
四面体的体积等于正方体的体积减去四个正三棱锥的体积,即为,故④错误.
故答案为:①③.
18.(1)证明见解析;(2)M点在上靠近P点的四等分点处.
(1)连接,由,可证明,,从而得平面,得证线线垂直;
(2)设设,则,根据棱锥的体积公式,利用体积法得出结论,由,,可得值.
【详解】
(1)连接且E是的中点,.
又平面平面,平面平面平面.
平面平面.
又为菱形,且分别为棱的中点,.
,又平面;
平面.
(2)如图,连接,
设,则,
,
,则,又.
.
解得,即M点在上靠近P点的四等分点处.
方法点睛:本题考查由线面垂直证明线线垂直,考查由体积法求线段的比值.若是棱锥棱上一点,则.三棱锥求体积时可以换底,这样求体积比较灵活简便.
19.(1)证明见解析;(2)1.
(1)由余弦定理可得,根据勾股定理的逆定理得,结合即可得出结果.
(2)由面面垂直的性质定理得平面,且,根据线线平行得出平面平面,进而得到与到底面的距离相等,结合棱锥体积公式即可.
【详解】
(1)证明:,,
又是等边三角形,
,
又,
在中,由余弦定理可得,
,
,故,
又,;
(2)解:取的中点,连接,
由,得,
又平面平面,
且平面平面,
平面,
且求得.
由,平面平面,
可得平面,
则与到底面的距离相等,
则四面体的体积.
(1)证明线线垂直的方法主要有:线面垂直的性质定理、勾股定理的逆定理或者采用空间向量法;
(2) 求三棱锥的体积时要注意三棱锥的每个面都可以作为底面,例如三棱锥的三条侧棱两两垂直,我们就选择其中的一个侧面作为底面,另一条侧棱作为高来求体积.
20.(1)证明见解析
(2)
(3)
(1)过点作面,过点作,证明面,可得面,进而可得,求出、、的长,由勾股定理逆定理可证明,再由线面垂直的判定定理即可求证;
(2)过点作面,由对称性可得点在直线上,即为与平面所成角,在中,由正弦定理求得,延长、交于点,可得为的中位线,在中,由余弦定理可得的值,进而可得的值,再计算即可求解;
(3)根据已知条件分析在上的投影,即可得的虚部.
(1)
过点作面,过点作,
因为边长为的等边三角形,且上底面与下底面相似,比边长之为,
所以,
在正三棱台中,连接,因为面,
则点必落在上,,
因为为等边三角形,是线段的中点,可得,
因为面,面,,所以面,
因为,所以面,所以,,
因为,所以是的中点,
因为,所以,
因为是的中点,所以,
所以,可得,
因为,,所以平面,
(2)
过点作面,由对称性可得点在直线上,
因为,
在中,由正弦定理可得:,
即,所以,所以,
因为为梯形的一条高,
所以即为与平面所成角,
因为,,,,
延长、交于点,
因为,,所以为的中位线,
所以,,
在中,由余弦定理可得:,
所以,
所以,
所以直线与平面所成角的正弦值为.
(3)
.
21.(1)证明见解析;(2)证明见解析.
(1)根据四边形ABCD是菱形可得 AB平面CDE,再结合AF平面CDE即可证明;
(2)根据已知条件结合线面平行性质得AFDE,再在线段ED上取一点G,使得EG=4,进而根据几何关系得AD⊥ED,AD⊥DC,即可通过AD⊥平面CDE证得结论.
【详解】
证明:(1)∵ 四边形ABCD是菱形,∴ABCD,
∵AB平面CDE,CD平面CDE,∴AB平面CDE,
又AF平面CDE,AF∩AB=A,∴平面ABF平面CDE.
(2)AF平面CDE,AF平面ADEF,平面ADEF∩平面CDE=DE,
∴AFDE.
在线段ED上取一点G,使得EG=4,则DG=2=AF,
又∵DGAF,∴四边形ADGF是平行四边形,
∴FG=AD=5,FGAD,
∵,∴,
∴EG⊥FG,∴AD⊥ ED.
∵∠ABC=90°,四边形ABCD是菱形,
∴AD⊥DC,
又DC∩DE=D,∴AD⊥平面CDE,
∵CE平面CDE,∴AD⊥CE.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
